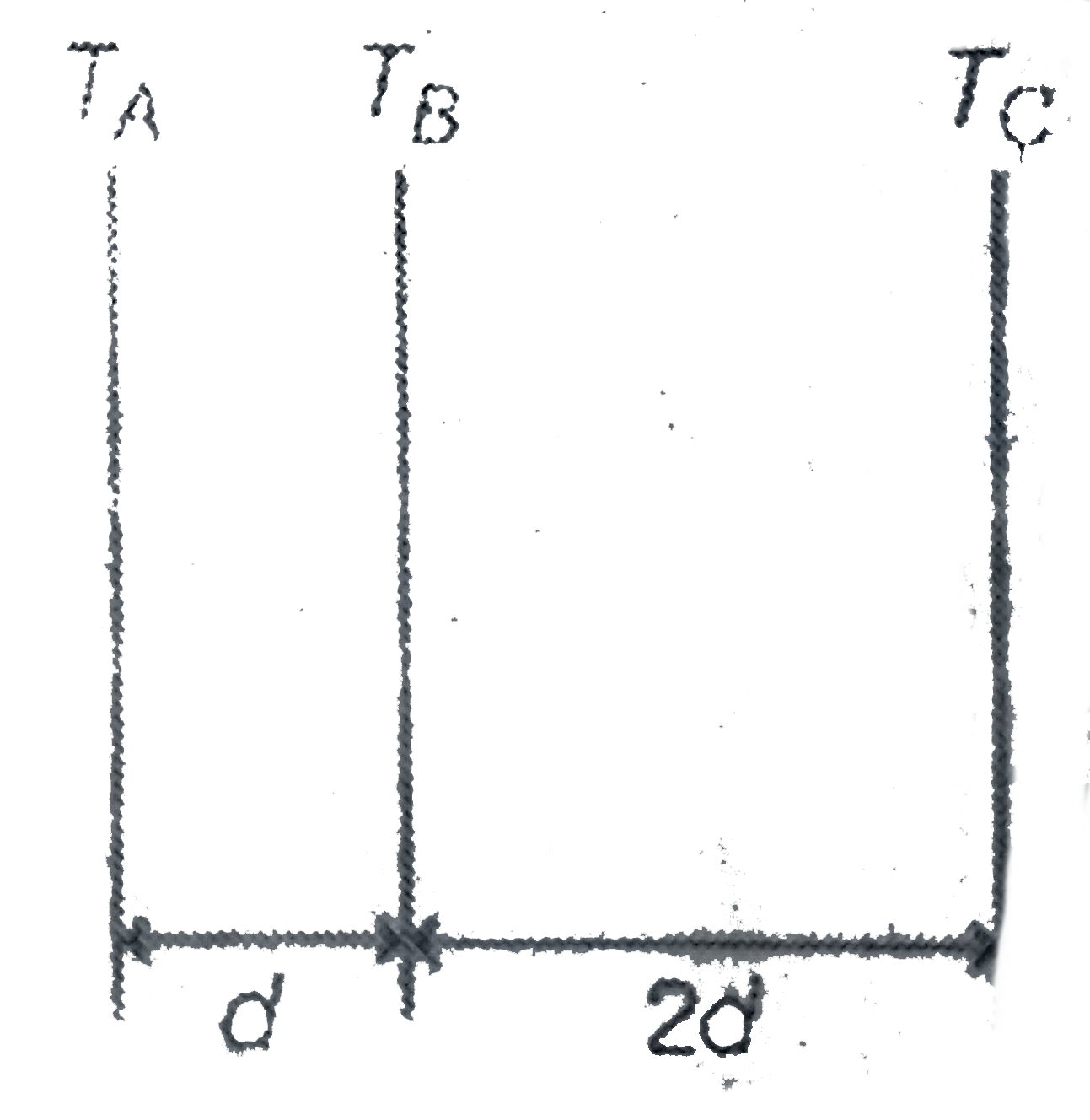
Two sheets of thickness d and 3d and of same area are joined together. Temperature TA,TB,TC shown in the figure are in geometric progression with common ration r=3. Then ratio of thermal conductivity of thinner to thicker sheet is

1
2
3
4
The correct Answer is:A
TB=3T
TC3TB=9TA
In steady state Pin=Pout
=K2A1(TB−TC3d)=−K1A(TA−TBd)
K23(−6TA)=K1(−2TA)
2K2=2K1
K1K2=11
Topper's Solved these Questions
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (A)
32 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (B)
3 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART- C
4 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
Three rods of the same length and the same area of the cross-section are joined. The temperature of two ends one T1 and T2 as shown in the figure.
 As we move along the rod the variation of temperature are as shown in the following [Rods are insulated from the surrounding except at the faces]
As we move along the rod the variation of temperature are as shown in the following [Rods are insulated from the surrounding except at the faces]

View SolutionTwo spherical concentric shells of radii r and 3r are kept at temperatures T1 and T2 as shown in the adjoining figure. If the space between the shells is filled with a liquid of thermal conductivity K, what will be the radial flow of heat through the liquid?

View Solution
Knowledge Check
Two sheets of thickness d and 2d and same area are touching each other on their face. Temperature TA,TB,TC shown are in geometric progression with common ratio r = 2. Then ratio of thermal conductivity of thinner and thicker sheet are
 A1B2C0.5D4
A1B2C0.5D4Two sheets of thickness d and 3d, are touching each other. The temperature just outside the thinner sheet is T1 and on the side of the thicker sheet is T3. The interface temperature is T2.T1,T2andT3 are in arithmetic progression. The ratio of thermal conductivity of thinner sheet to thicker sheet is
A1:3B3:1C2:3D3:9If a,b,c are in geometric progression and a,2b,3c are in arithmetic progression, then what is the common ratio r such that 0<r<1 ?
A13B12C14D18
A thick spherical shell of inner and outer radii r and R respectively has thermal conductivity k=ρxn , where ρ is a constant and x is distance from the centre of the shell. The inner and outer walls are maintained at temperature T1 and T2(<T1)
(a) Find the value of number n (call it n0) for which the temperature gradient remains constant throughout the thickness of the shell.
(b) For n=n0, find the value of x at which the temperature is T1+T22
(c) For n=n0, calculate the rate of flow of heat through the shell.
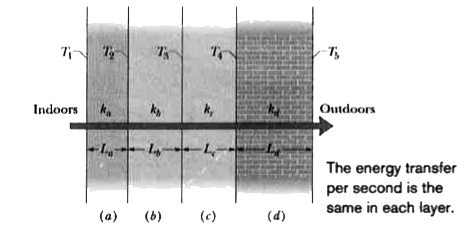
View SolutionFigure shows the cross section of a wall made of white pine of thickness La and brick of thickness Ld==2.0La , sandwiching two layers of unknonw material with identical thicknesses and thermal conductivities. The thermal conductivity of the pine is ka and that of the brick is kd(=5.0ka). The face area A of the wall is unknown. Thermal conduction through the wall has reached the steady state, the only known interface temperatures are T1=25∘C,T2=20∘C, and T5=−10∘C. What is interface temperature T4 ?
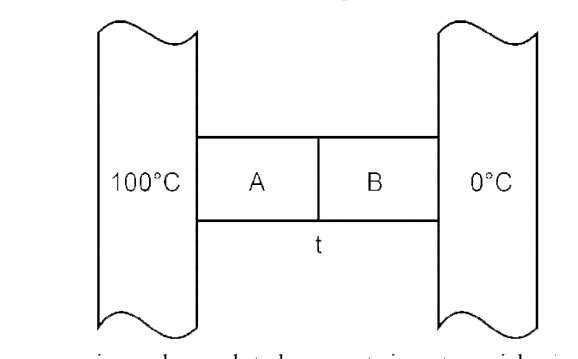
View SolutionTwo metal cubes A and B of same size are arranged as shown in Figure. The extreme ends of the combination are maintened at the indicated temperatures. The arrangement is thermally insulted. The coefficients of thermal conductivity of A and B are 300W/m∘Cand200W/m∘C, respectively. After steady state is reached the temperature t of the interface will be ......
View SolutionTwo walls of thickness d and d and thermal conductivities k and k are in contact. In the steady state, if the temperature at the outer T1 and T2 , the temperature at the common wall is
View SolutionTwo rods A and B of same cross-sectional area A and length l are connected in series between a source (T1=100∘C) and a sink (T2−0∘C) as shown in figure. The rod is laterally insulated.
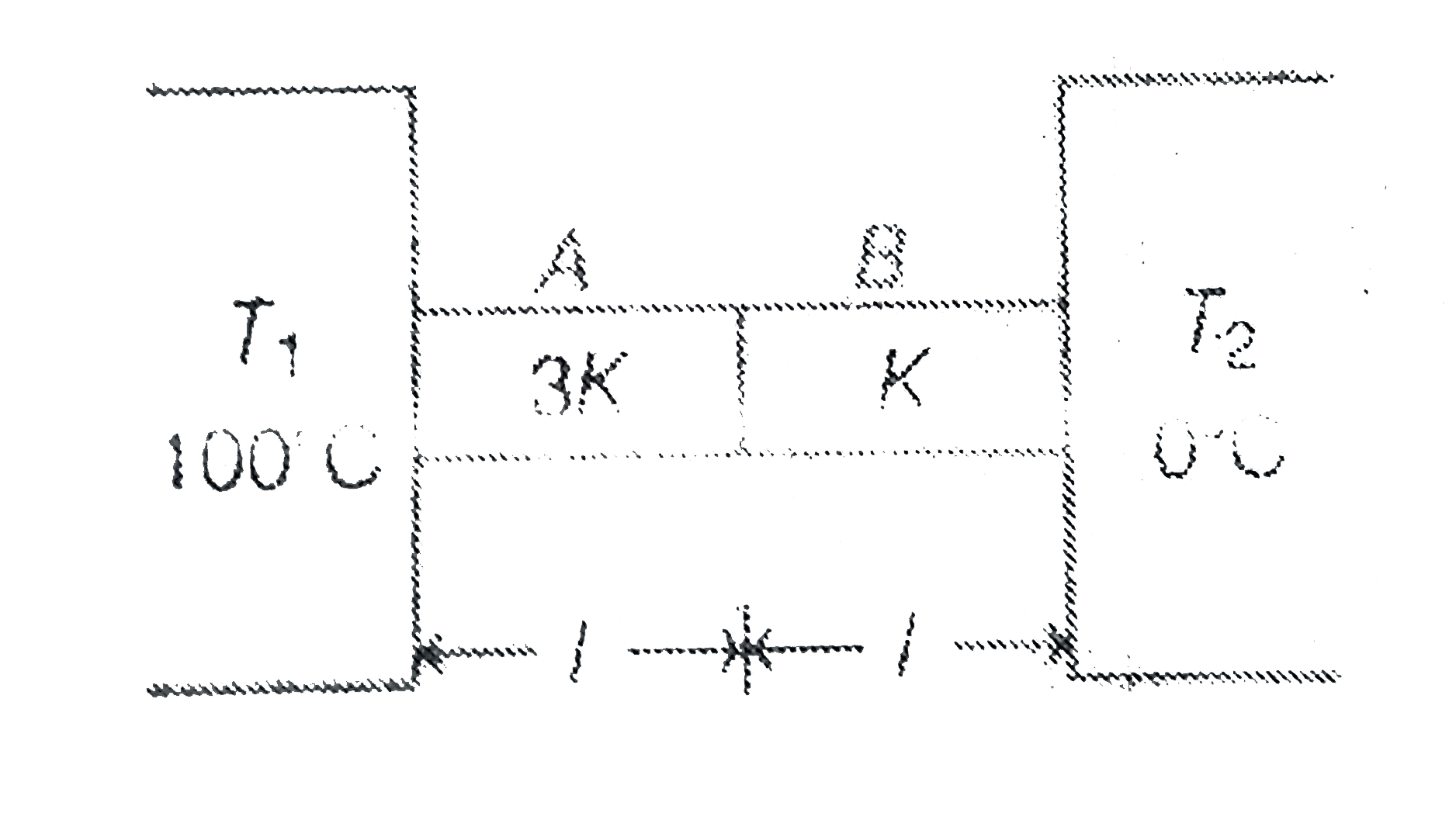
The ratio of the thermal resistance of the rods is
View Solution
