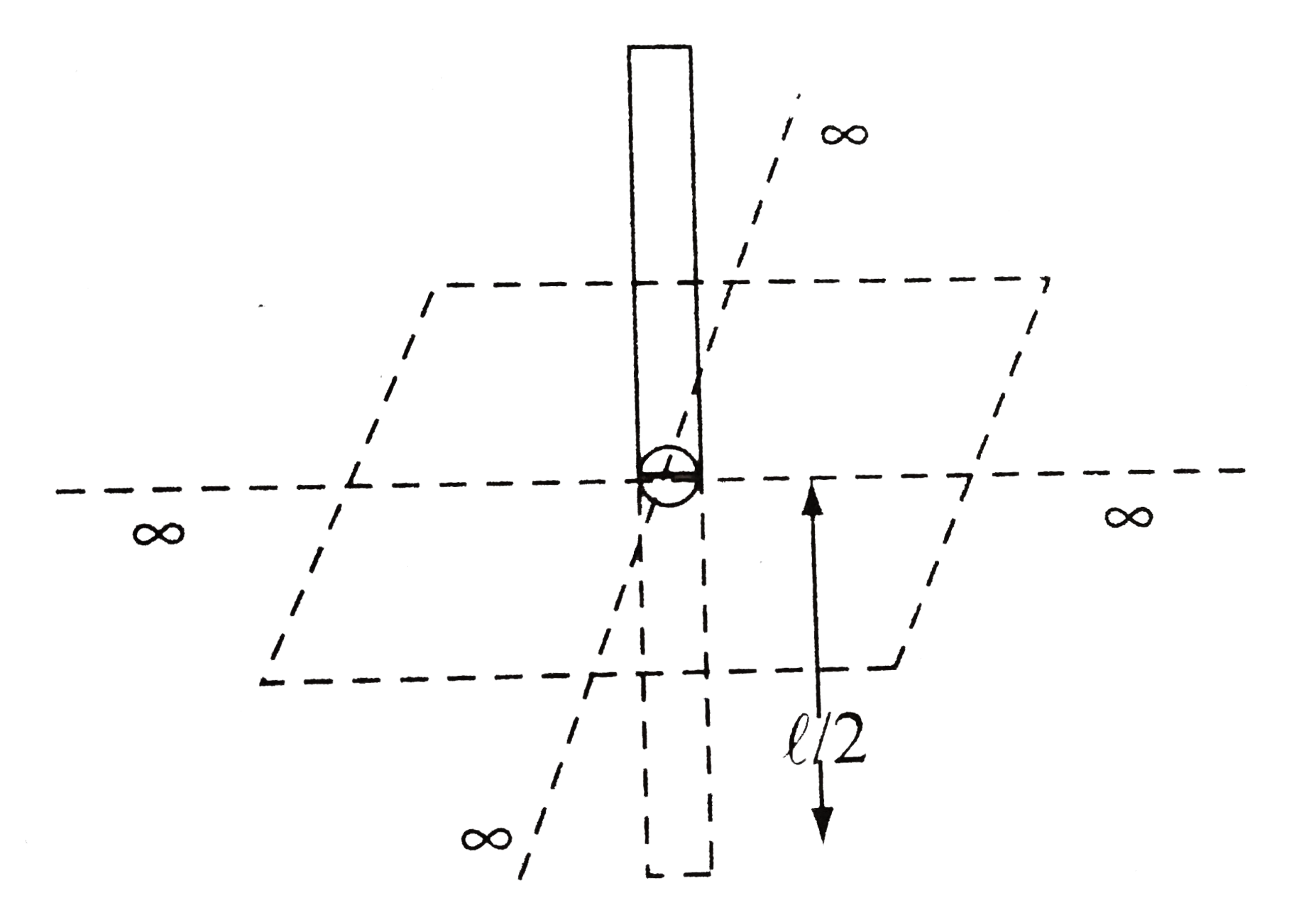
An infinite nonconducting sheet has surface charge density s. There is a small hole in the sheet as shown in the figure. A uniform rod of length l having linear charge density λ is hinged in the hole as shown. If the mass of the rod is m, then the time period of oscillation for small angular displacement is
π√mε03σλ
2π√2mε03σλ
π2√mε03σλ
4π√mε03σλ
The correct Answer is:B
r−2(σ2ε0λdx)xsinθ=σε0λ∫l/2oxdxsinθ=σ2ε0λl24sinθ
r=Ia or a=−τ/I=σ2ε0λl2412ml2sinθ
a=−(3σλ2mε0θ) (for small angle)
τ=2πω=2π√2mε03σλ
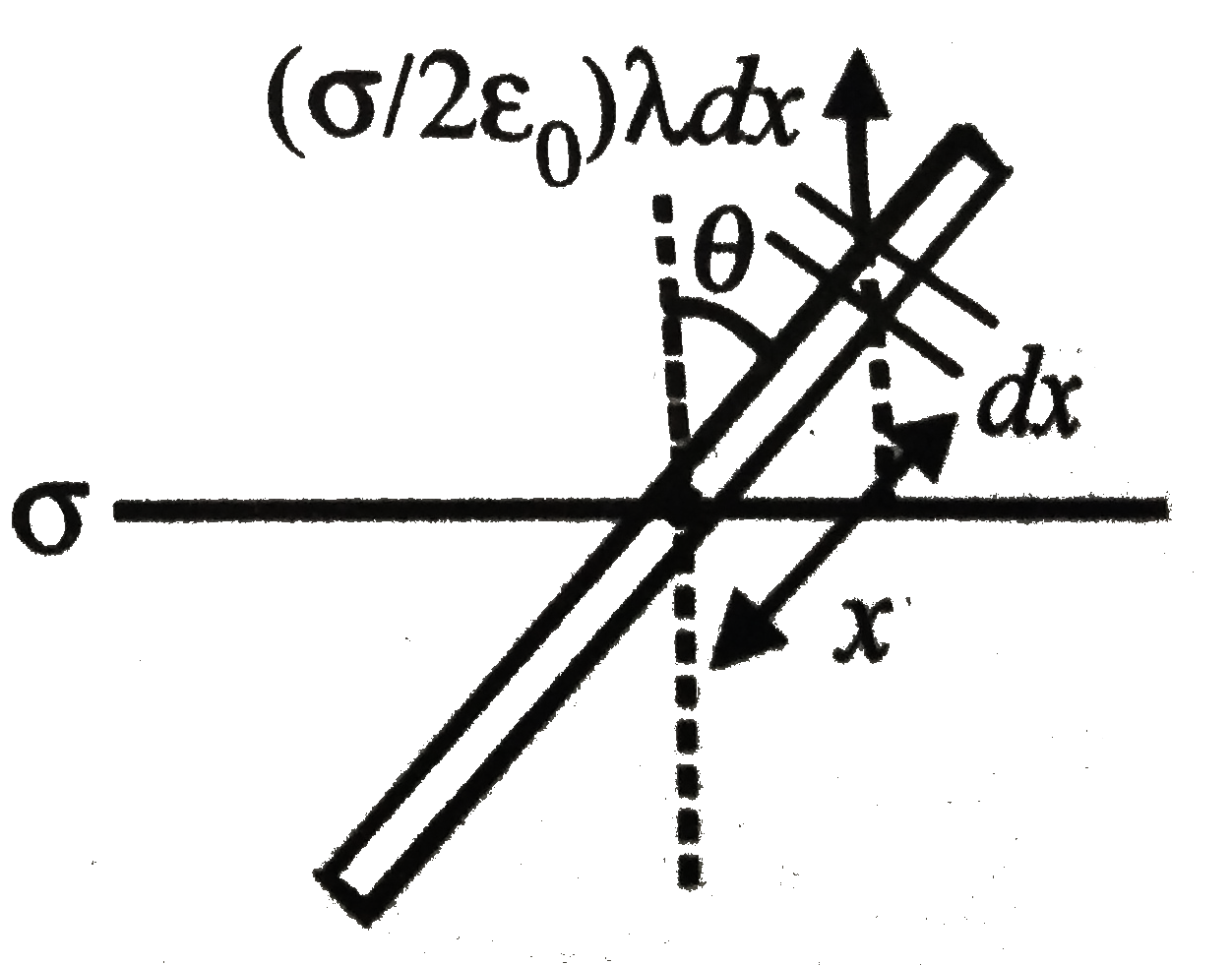
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 3Book:CENGAGE PHYSICSChapter:MISCELLANEOUS VOLUME 3Exercise:Multiple Correct Answer type
Explore 109 Videos
- MISCELLANEOUS VOLUME 3Book:CENGAGE PHYSICSChapter:MISCELLANEOUS VOLUME 3Exercise:Assertion and Reason Type
Explore 8 Videos
- MECHANICAL PROPERTIES OF SOLIDSBook:CENGAGE PHYSICSChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:Question Bank
Explore 4 Videos
- MISCELLANEOUS VOLUME 5Book:CENGAGE PHYSICSChapter:MISCELLANEOUS VOLUME 5Exercise:Integer
Explore 12 Videos
Similar Questions
A uniform rod of length 1.00 m is suspended through an end and is set into oscillation with small amplitude under gravity. Find the time period of oscillation.
View SolutionA semi-infinite insulating rod has linear charge density λ. The electric field atthe pointPshown in figure-1.418 is:

View Solution
Knowledge Check
A large nonconducting sheet M is given a uniform charge density. Two unchared small metal rods A and B are placed near the sheet as shown in figure
 AM attracts ABA attract BCM attracts BDB repels A
AM attracts ABA attract BCM attracts BDB repels AA uniform rod of length 2.0 m is suspended through an end and is set into oscillation with small amplitude under gravity. The time period of oscillation is approximately
A1.60secB1.80 secC2.0 secD2.40 secIn which of the following cases the centre of mass of a rod is certainly not at its centre ?
Athe density continuously increases from left to rightBthe density continuously decreases from left to righCthe density decreases from left to right upto the centre and then increasesDthe density increases from left to right upto the centre and then decreases
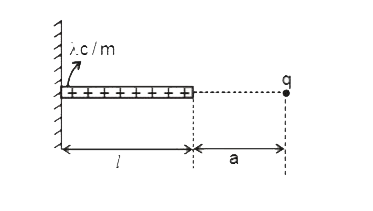
Find the total force on charge q due to a charge rod having linear charge density λCm placed as shown in figure.
View SolutionWhat is the electric field intensity at any point on the axis of a charged rod of length 'L' and linear charge density λ? The point is separated from the nearer end by a.
View SolutionAn infinite nonconducting sheet has a surface charge density of σ=0.10μC/m2 on one side. How far apart are equipotential surfaces whose potentials differ by 50 V?
View SolutionIn the figure shown S is a large nonconducting sheet of uniform charge density σ. A rod R of length l and mass 'm' is parallel to the sheet and hinged at its mid point. The linear charge densities on the upper and lower half of the rod are shown in the figure. Find the angular acceleration of the rod just after it is released.
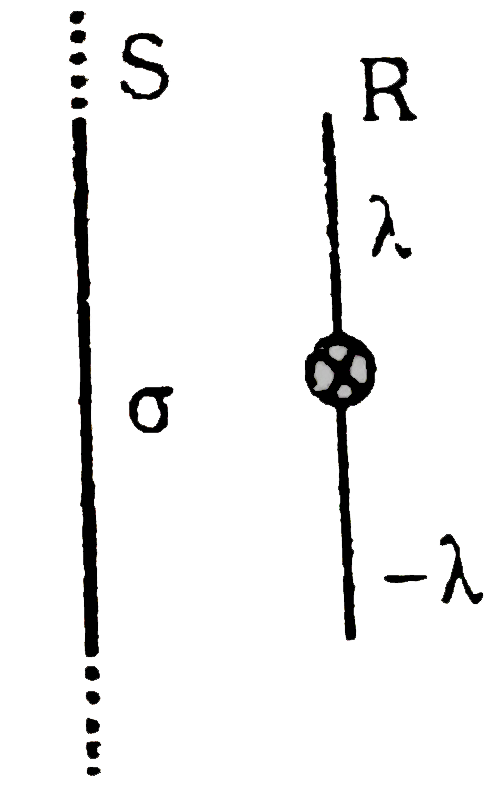
View SolutionIn the figure shown S is a large nonconducting sheet of uniform charge density σ. A rod R of length l and mass 'm' is parallel to the sheet and hinged at its point. The linear charge densities on the upper and lower half of the rod are shown in the figure. Find the angular acceleration of the rod just after it is released
[3σλ2m∈0]
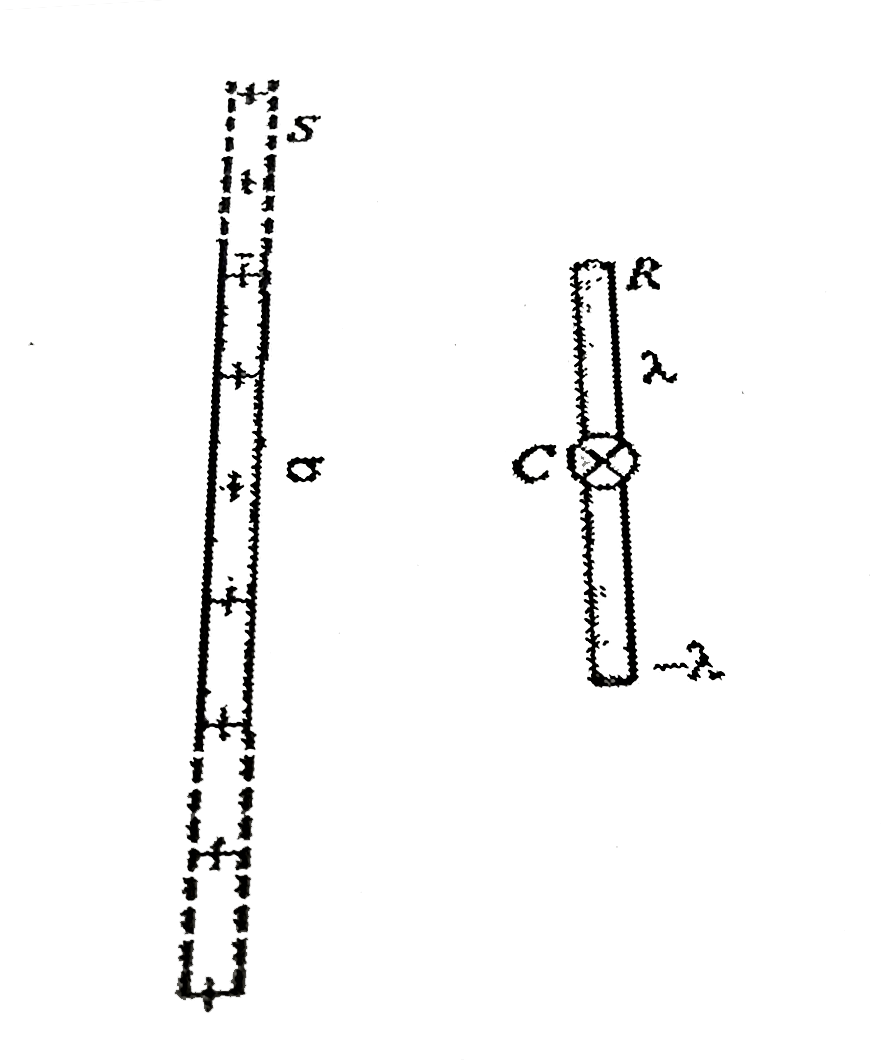
View Solution

