An infinite nonconducting sheet has a surface charge density of σ=0.10μC/m2 on one side. How far apart are equipotential surfaces whose potentials differ by 50 V?
To solve the problem of finding the distance between equipotential surfaces whose potentials differ by 50 V due to an infinite non-conducting sheet with a surface charge density of σ=0.10μCm², we can follow these steps:
Step 1: Understand the Electric Field due to the Infinite Sheet
The electric field (E) produced by an infinite non-conducting sheet with surface charge density σ is given by the formula:
\(
E = \frac{\sigma}{2\epsilon_0}
\)
where ε0 is the permittivity of free space, approximately \(8.85 \times 10^{-12} \, \text{C}^2/\text{N m}^2\).
Step 2: Calculate the Electric Field
Given that σ=0.10μCm²=0.10×10−6Cm², we can substitute this value into the formula for the electric field:
\(
E = \frac{0.10 \times 10^{-6}}{2 \times 8.85 \times 10^{-12}}
\)
Calculating this gives:
\(
E = \frac{0.10 \times 10^{-6}}{1.77 \times 10^{-11}} \approx 5645.7 \, \text{N/C}
\)
Step 3: Relate Potential Difference to Distance
The potential difference (ΔV) between two points in an electric field is related to the electric field and the distance (d) between those points by the equation:
\(
\Delta V = E \cdot d
\)
We need to find the distance d for a potential difference of 50V.
Step 4: Rearrange the Equation to Solve for Distance
Rearranging the equation gives:
\(
d = \frac{\Delta V}{E}
\)
Step 5: Substitute the Known Values
Substituting ΔV=50V and E≈5645.7NC into the equation:
\(
d = \frac{50}{5645.7} \approx 0.00885 \, \text{m} \, \text{or} \, 8.85 \, \text{mm}
\)
Final Answer
The distance between the equipotential surfaces whose potentials differ by 50 V is approximately 8.85 mm.
---
The electric field (E) produced by an infinite non-conducting sheet with surface charge density σ is given by the formula:
\(
E = \frac{\sigma}{2\epsilon_0}
\)
where ε0 is the permittivity of free space, approximately \(8.85 \times 10^{-12} \, \text{C}^2/\text{N m}^2\).
Given that σ=0.10μCm²=0.10×10−6Cm², we can substitute this value into the formula for the electric field:
\(
E = \frac{0.10 \times 10^{-6}}{2 \times 8.85 \times 10^{-12}}
\)
Calculating this gives:
\(
E = \frac{0.10 \times 10^{-6}}{1.77 \times 10^{-11}} \approx 5645.7 \, \text{N/C}
\)
The potential difference (ΔV) between two points in an electric field is related to the electric field and the distance (d) between those points by the equation:
\(
\Delta V = E \cdot d
\)
We need to find the distance d for a potential difference of 50V.
Rearranging the equation gives:
\(
d = \frac{\Delta V}{E}
\)
Substituting ΔV=50V and E≈5645.7NC into the equation:
\(
d = \frac{50}{5645.7} \approx 0.00885 \, \text{m} \, \text{or} \, 8.85 \, \text{mm}
\)
The distance between the equipotential surfaces whose potentials differ by 50 V is approximately 8.85 mm.
Topper's Solved these Questions
- ELECTRIC POTENTIALBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - SAMPLE PROBLEM 24.04 Finding the potential change from the electric field
1 Videos
- ELECTRIC POTENTIALBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - SAMPLE PROBLEM 24.05 Finding electric potential
1 Videos
- ELECTRIC POTENTIALBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - SAMPLE PROBLEM 24.02 Distance, velocity, closest separation for charged particle projected from ∞ towards fixed particle
1 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Questions (Integer Type )
3 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - PRACTICE QUESTIONS (Integer Type)
14 Videos
Similar Questions
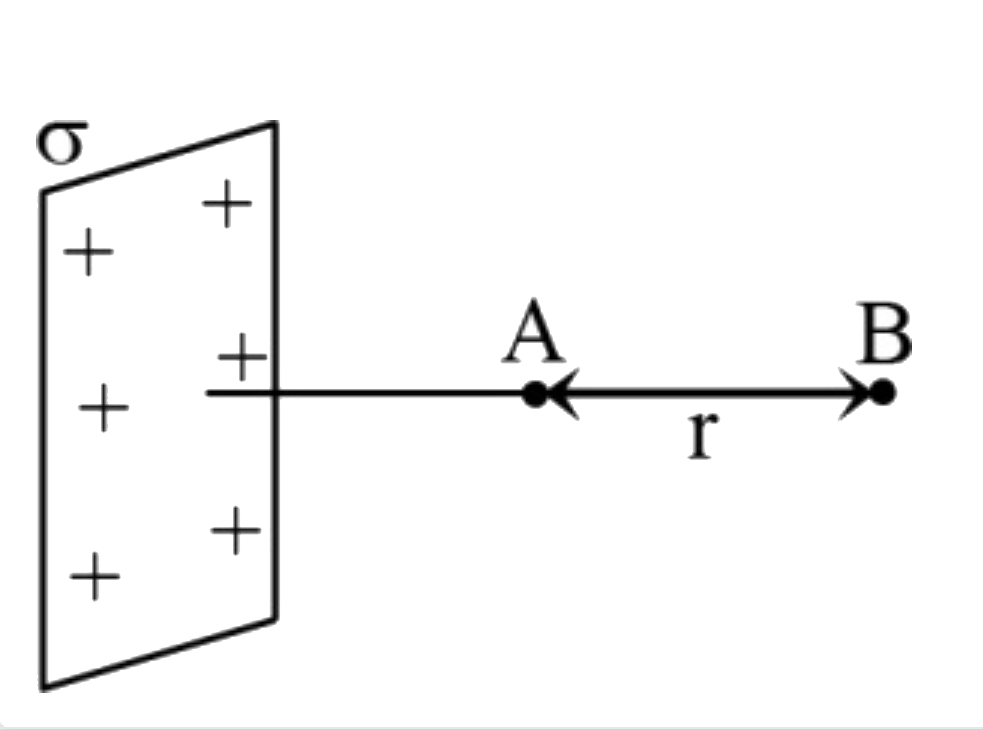
An infinite conducting sheet has surface charge density σ. The distance between two points is r. The potential difference (VA−VB) between these point is
View SolutionAn infinite plane sheet of charge density 10−8Cm−2 is held in air. In this situation how far apart are two equipotenitial surfaces, whose p.d is 5 V ?
View Solution
Knowledge Check
An infinite sheet of charge has a surfaces charge density of 10−7Cm2. The separation between two equipotential surfce whose potentials differ by 5V is
A0.64cmB0.88mmC0.32cmD5×10−7mAn infinite sheet of charge has surface charge density σ . The separation between two equipotential surfaces, whose potential differ by V is:
AσV2∈0B2∈0VσC∈0VσD2σ∈0VAn infinite nonconducting sheet has surface charge density s. There is a small hole in the sheet as shown in the figure. A uniform rod of length l having linear charge density λ is hinged in the hole as shown. If the mass of the rod is m, then the time period of oscillation for small angular displacement is
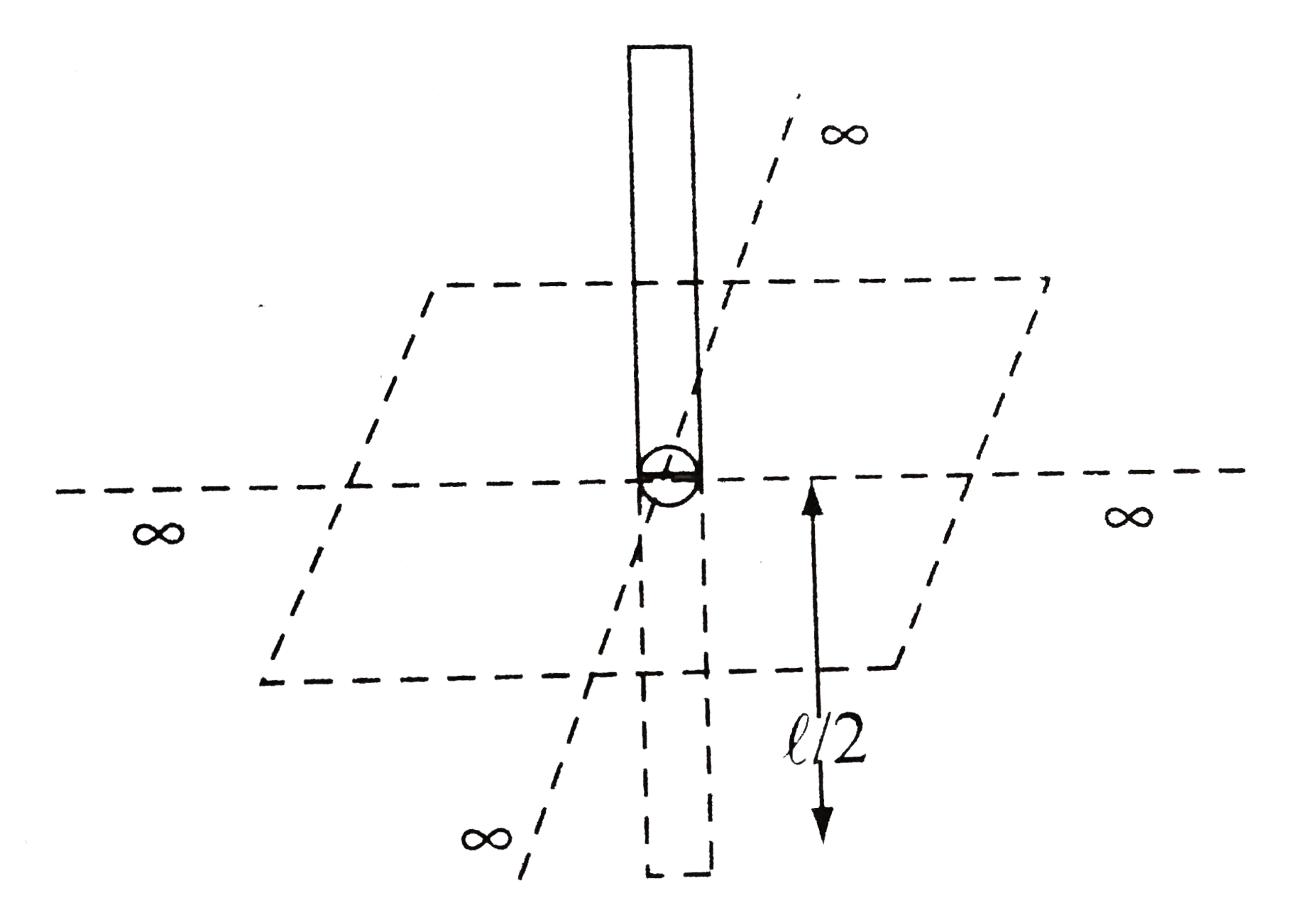 Aπ√mε03σλB2π√2mε03σλCπ2√mε03σλD4π√mε03σλ
Aπ√mε03σλB2π√2mε03σλCπ2√mε03σλD4π√mε03σλ
An infinite nonconducting sheet with a uniform surface charge density sets up parallel equipotential surfaces. Any pair of surfaces differing by 25.0 V are separated by 8.80 mm. (a) What is the magnitude of the surface charge density? (b) If an electron is released near the sheet, does it tend to move from higher to lower potential or vice versa ?
View SolutionElectric field due to an infinite non-conducting sheet of surface charge density σ, at a distance r from it is
View SolutionAn infinite changed sheet has 10−7Cm−2 surface density of change .How far apart are the equipotential surface differing by 5 voits ?
[Hint: Elwctri intensity =rate of fall of potential .]
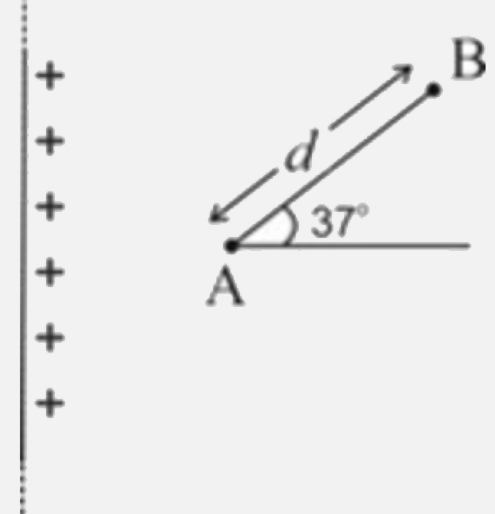
View SolutionAn infinite thin non - conducting sheet has uniform surface charge density σ. Find the potential difference VA−VB between points A and B as shown in the figure. The line AB makes an angle of 37∘ with the normal to the sheet. (sin37∘=35)
View SolutionTwo infinite parallel,non- conducting sheets carry equal positive charge density σ ,One is placed on the other at distance x=a Take potential V=0 at x=0 then
View Solution
