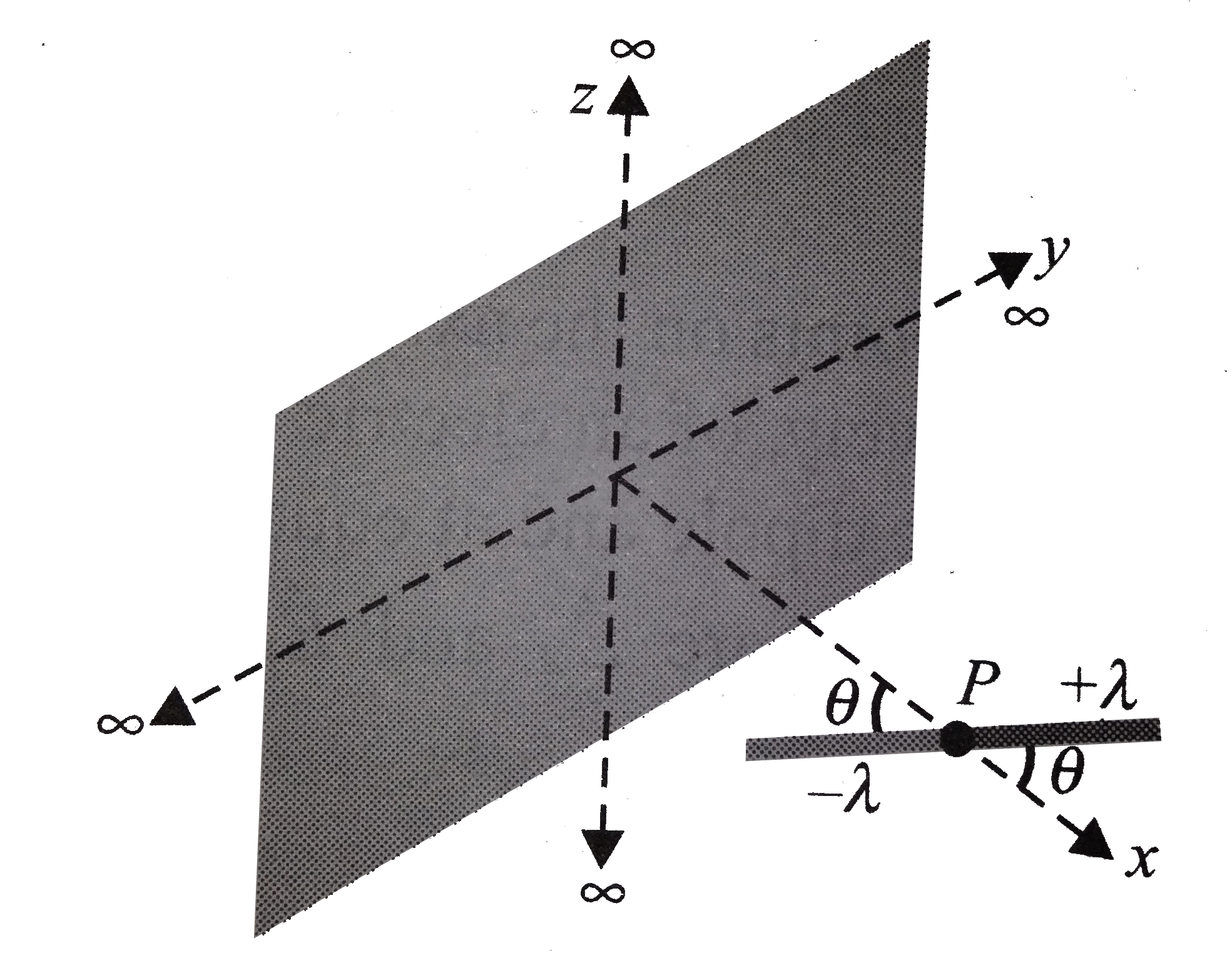
A large sheet carries uniform surface charge density σ . A rod of length 2l has a linear charge density lamba on one half and −λ on the second half. The rod is hinged at the midpoint O and makes an angle θ with the normal to the sheet. The torque experience by the rod is
0
σλl22ε0sinθ
σλl2ε0sinθ
σλl2ε0
The correct Answer is:B
τ=(λlE)lsinθ
=λl2σ2ε0=σλl22εsinθ

Topper's Solved these Questions
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Multiple Correct
8 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Comprehension
25 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Subjective
32 Videos
- COMMUNICATION SYSTEMBOOK - CENGAGE PHYSICSCHAPTER - COMMUNICATION SYSTEMEXERCISE - QUESTION BANK
19 Videos
- Current ElectricityBOOK - CENGAGE PHYSICSCHAPTER - Current ElectricityEXERCISE - QUESTION BANK
40 Videos
Similar Questions
In the figure shown S is a large nonconducting sheet of uniform charge density σ. A rod R of length l and mass 'm' is parallel to the sheet and hinged at its mid point. The linear charge densities on the upper and lower half of the rod are shown in the figure. Find the angular acceleration of the rod just after it is released.
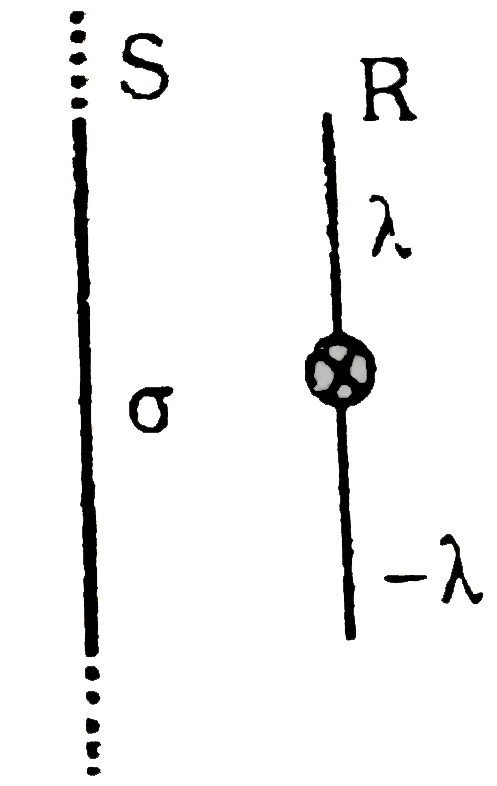
View SolutionIn the figure shown, S is a large non-conducting sheet of uniform charge density σ. A rod R of length I and mass m is parallel to the sheet and hinged at its midpoint. The linear charge densities on the upper and lower half of the rod are shown in the figure. The angular acceleration of the rod just after it is released is pσλqmɛo. Find pq.
'(##CEN_KSR_PHY_JEE_C18_E01_031_Q16##)'
View Solution
Knowledge Check
A ring carries a uniform linear charge density on one half and the linear charge density of same magnitude but opposite sign on the other half.
AThe component of electric field along the axis at all points on the axis is zeroBthe electric field along the axis and on the axis is zero only at the centreCthe resultant field at the centre is zeroDthe resultant field at all points on the axis is zeroIn the figure shown there is a large sheet of charge of uniform surface charge density'σ'.A charge particle of charge '−q' and mass 'm' is projected from a point A on the sheet with a speed 'u' with the angle of projection such that it lands at maximum distance from A on the sheet. Neglecting gravity, find the time flight
 A2√2mvε0σqB√2mvε05σqCmvε0√2σqDmvε02√2σq
A2√2mvε0σqB√2mvε05σqCmvε0√2σqDmvε02√2σq
In the figure shown S is a large nonconducting sheet of uniform charge density σ. A rod R of length l and mass 'm' is parallel to the sheet and hinged at its point. The linear charge densities on the upper and lower half of the rod are shown in the figure. Find the angular acceleration of the rod just after it is released
[3σλ2m∈0]
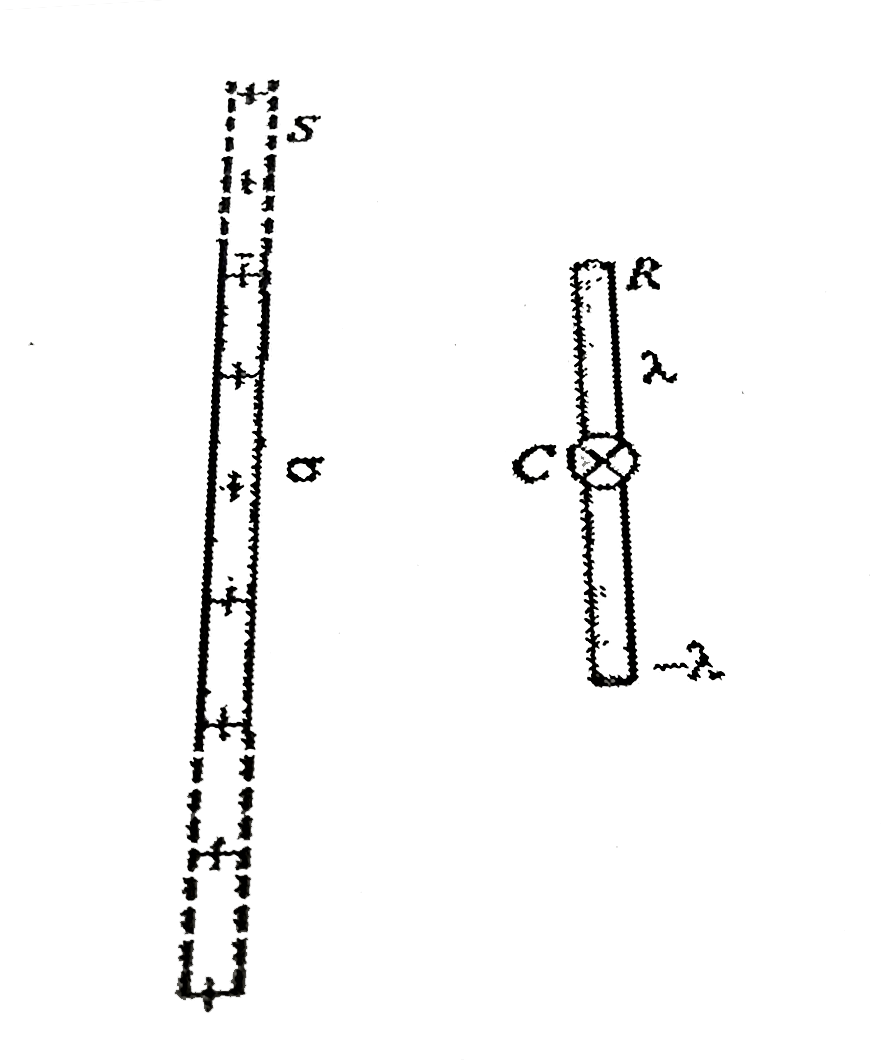
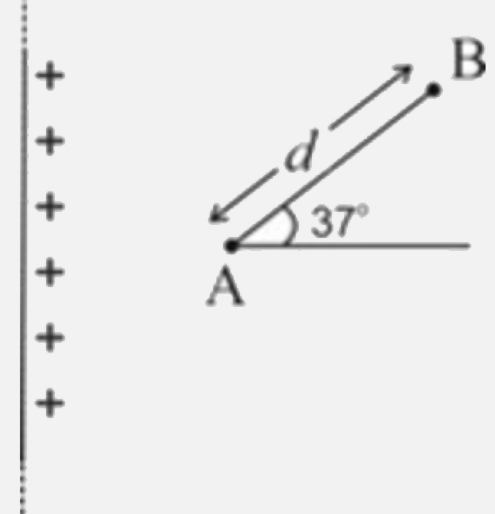
View SolutionAn infinite thin non - conducting sheet has uniform surface charge density σ. Find the potential difference VA−VB between points A and B as shown in the figure. The line AB makes an angle of 37∘ with the normal to the sheet. (sin37∘=35)
View SolutionA uniform rod AB of mass m and length l is hinged at its mid point C. The left half (AC) of the rod has linear charge density −λ and the right half (CB) has +λ where λ is constant. A large non conducting sheet of uniform surface charge density σ is also present near the rod. Initially the rod is kept perpendicular to the sheet. The end A of the rod is initialy at a distance d. Now the rod is rotated by a small angle in the plane of the paper and released. Prove that the rod will perform SHM and find its time period.

View SolutionAn insulting thin rod of length l has a linear charge density ρ(x)=ρ0xl on it. The rod is rotated about an axis passing through the origin (x=0) and perpendicular to the rod. If the rod makes n rotations per second, then the time averaged magnetic moment of the rod is :
View SolutionWhat is the electric field intensity at any point on the axis of a charged rod of length 'L' and linear charge density λ? The point is separated from the nearer end by a.
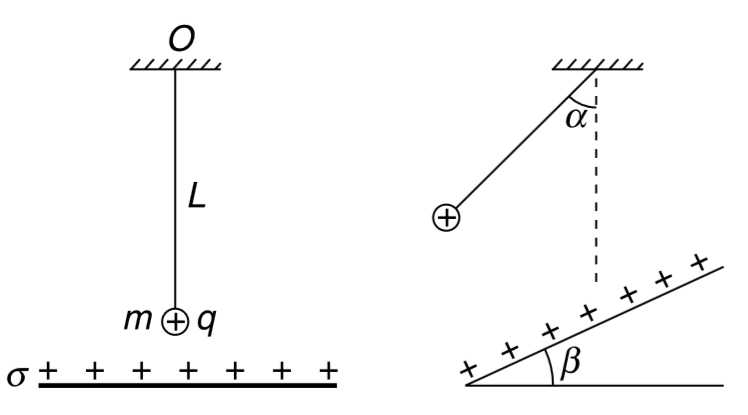
View SolutionA pendulum has a bob of mass m carrying a positive charge q. Length of the pendulum string is L. Beneath the pendulum there is a large horizontal dielectric sheet of charge having uniform surface charge density of σC/m2. [figure (i)] (a) Find the time period of small oscillations for the pendulum (b) Now the dielectric sheet of charge is tilted so as to make an angle β with horizontal. Find the angle (a) that the thread makes with vertical in equilibrium position. Find time period of small oscillations in this case. [figure (ii)]
View Solution
