Three identical point charges, each of mass m and charge q, hang from three strings as shown in fig. The value of q in term of m, L, and q is
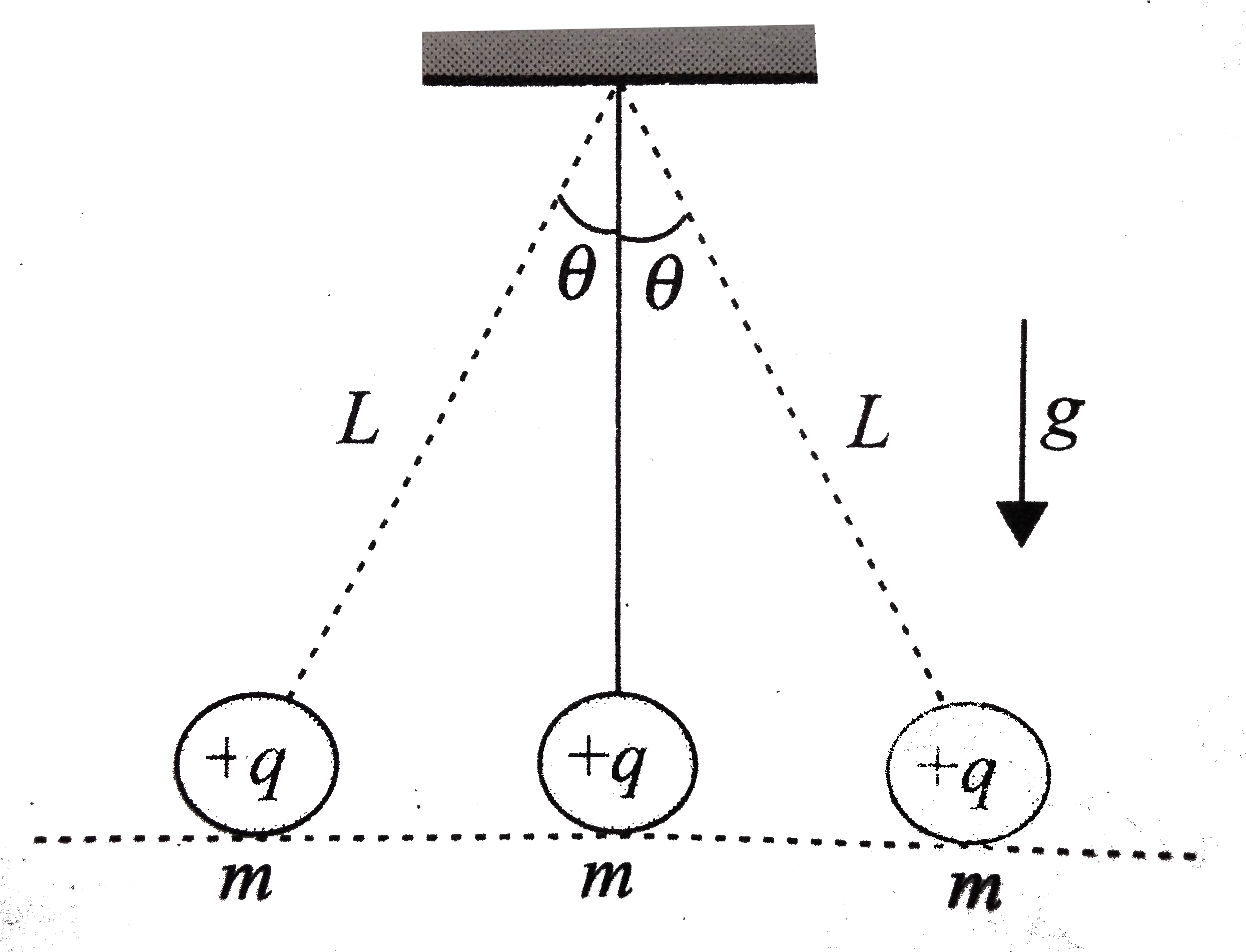
q=√(16/5)πε0mgL2sin2θtanθ
q=√(16/15)πε0mgL2sin2θtanθ
q=√(15/16)πε0mgL2sin2θtanθ
none of these
The correct Answer is:A
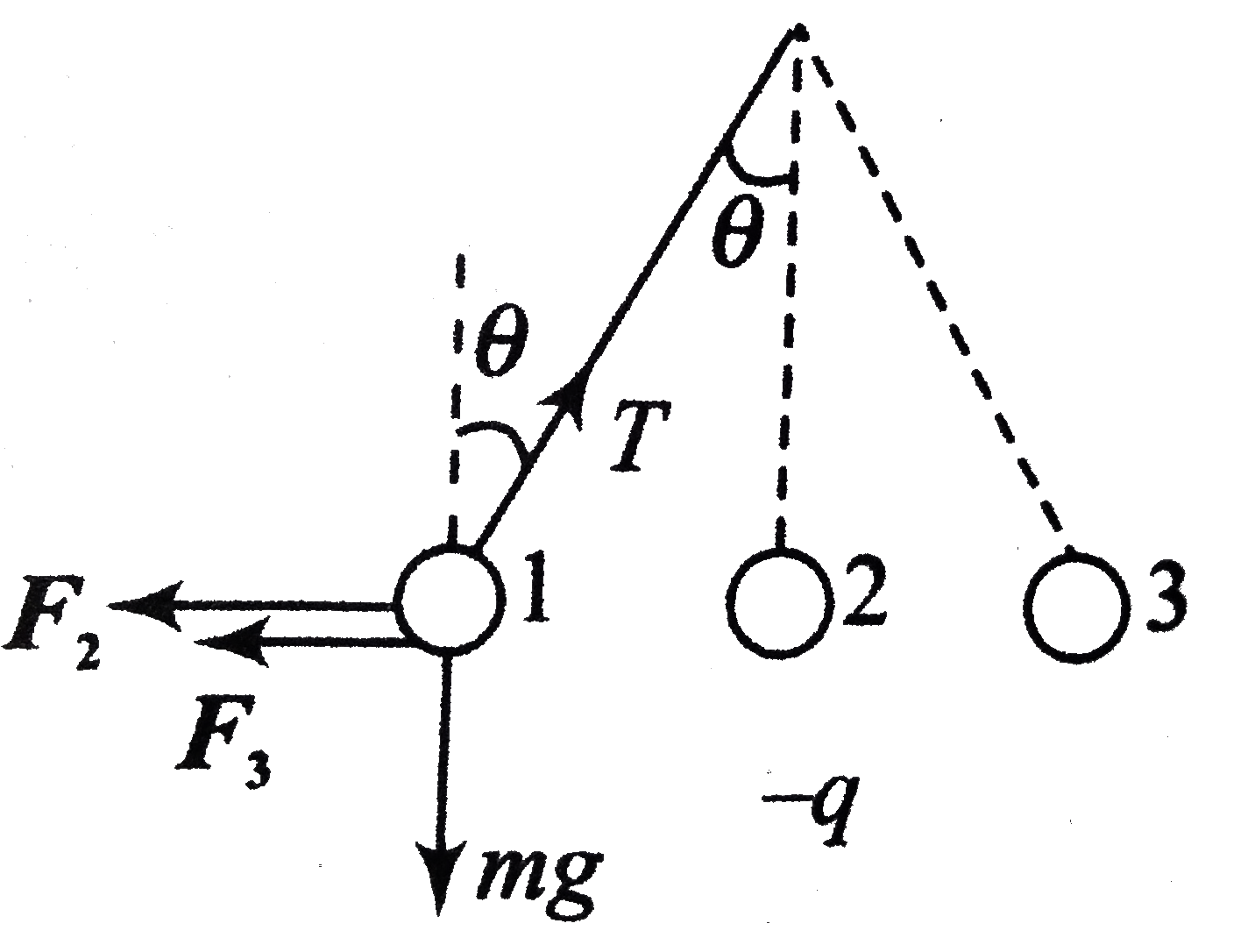
Fe=F2+F3
=kq2(Lsinθ)2+2kq2(2Lsinθ)2
Fe=54kq2L2sin2θ …(i)
Tsinθ=Fe …(ii)
Tcosθ=mg (iii)
from (i), (ii) and (iii)
q=√165πε0L2sin2θtanθ
Topper's Solved these Questions
- COULOMB LAW AND ELECTRIC FIELDBook:CENGAGE PHYSICSChapter:COULOMB LAW AND ELECTRIC FIELDExercise:Multiple Correct
Explore 8 Videos
- COULOMB LAW AND ELECTRIC FIELDBook:CENGAGE PHYSICSChapter:COULOMB LAW AND ELECTRIC FIELDExercise:Comprehension
Explore 25 Videos
- COULOMB LAW AND ELECTRIC FIELDBook:CENGAGE PHYSICSChapter:COULOMB LAW AND ELECTRIC FIELDExercise:Subjective
Explore 32 Videos
- COMMUNICATION SYSTEMBook:CENGAGE PHYSICSChapter:COMMUNICATION SYSTEMExercise:QUESTION BANK
Explore 19 Videos
- Current ElectricityBook:CENGAGE PHYSICSChapter:Current ElectricityExercise:QUESTION BANK
Explore 40 Videos
Similar Questions
Two identical small bodies each of mass m and charge q are suspended from two strings each of length l from a fixed point. This whole system is taken into an orbiting artificial satellite, then find the tensio in strings
View SolutionTwo identical small charged spheres, each having a mass m, hang in equilibrium as shown in fig. the ligth of each string is l, and the angle made by any string with the vertical is θ. Find the magnitude of the charge on each sphere.
View Solution
Knowledge Check
Three identical point charges, q, are placed at the vertices of an equilateral triangle as shown in the figure. The length of each side of the triangle is d. Determine the magnitude and direction of the total electrostatic force on the charge at the top of the triangle.
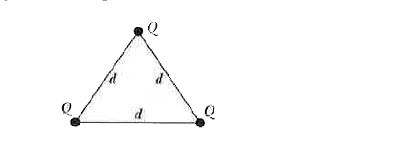 AQ2√34πε0d2, directed upwardBQ2√34πε0d2, directed downwardCQ2√32πε0d2, directed upwardDQ2√32πε0d2, directed downward
AQ2√34πε0d2, directed upwardBQ2√34πε0d2, directed downwardCQ2√32πε0d2, directed upwardDQ2√32πε0d2, directed downwardTwo identical small bodies each of mass m and charge q are suspended from two strings each of length l from a fixed point. This whole system is taken into an orbiting artificial satellite, then find the tensio in strings
AKq2l2+2mgBKq24l2+2mgCKq2l2DKq24l2Three point charges each of value +q are placed on three vertices of a square of side a metre. What is the magnitude of the force on a point charge of value −q coulomb placed at the centre of the square?
A(14πε0)(qa)2B(12πε0)(2qa)2C(12πε0)(qa)2D(14πε0)(2qa)2
Two identical point charges q of mass m each are suspended through strings of equal length l from a common point of suspension. Find the charge q if angle subtended by the strings with the vertical is θ, when point charges are in a state of equilibrium.
View SolutionThree point charges +q, +2q and Q are placed at the three vertices of an equilateral triangle. Find the value of charge Q (in terms of q), so that electric potential energy of the system is zero.
View SolutionTwo identical spheres of mass m and charge q are suspended from a common point by two threads of the same length l and it is found that threads make an angle θ with the vertical when the spheres are in equilibrium . Calculate the value of q.
View SolutionA particle having charge Q and mass M = 2 m is tied to two identical particles, each having mass m and charge q. The strings are of equal length, l each, and they are inextensible. The system is held at rest on a smooth horizontal surface (with string taut) in a position where the strings make an angle of 60∘ between them. From this position the system is released. (a) Find the amplitude of oscillation of M (b) Find maximum speed acquired by M (c) Find tension in the string when all the three particles get in one straight line.
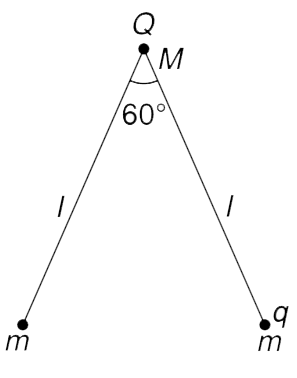
View SolutionThree point charges, each with charge q and mass 'm', are connected by three strings of equal length 'e whose other end is connected to a fixed point P. They form an equilateral triangle of side 'a' in a horizontal plane. The tension in each string will be
View Solution

