The direction (θ) of →E at point P due to uniformly charged finite rod will be

At an angle 30∘ from the x-axis
45∘ from the x-axis
60∘ from the x-axis
none of these
The correct Answer is:A
Using symmetry property
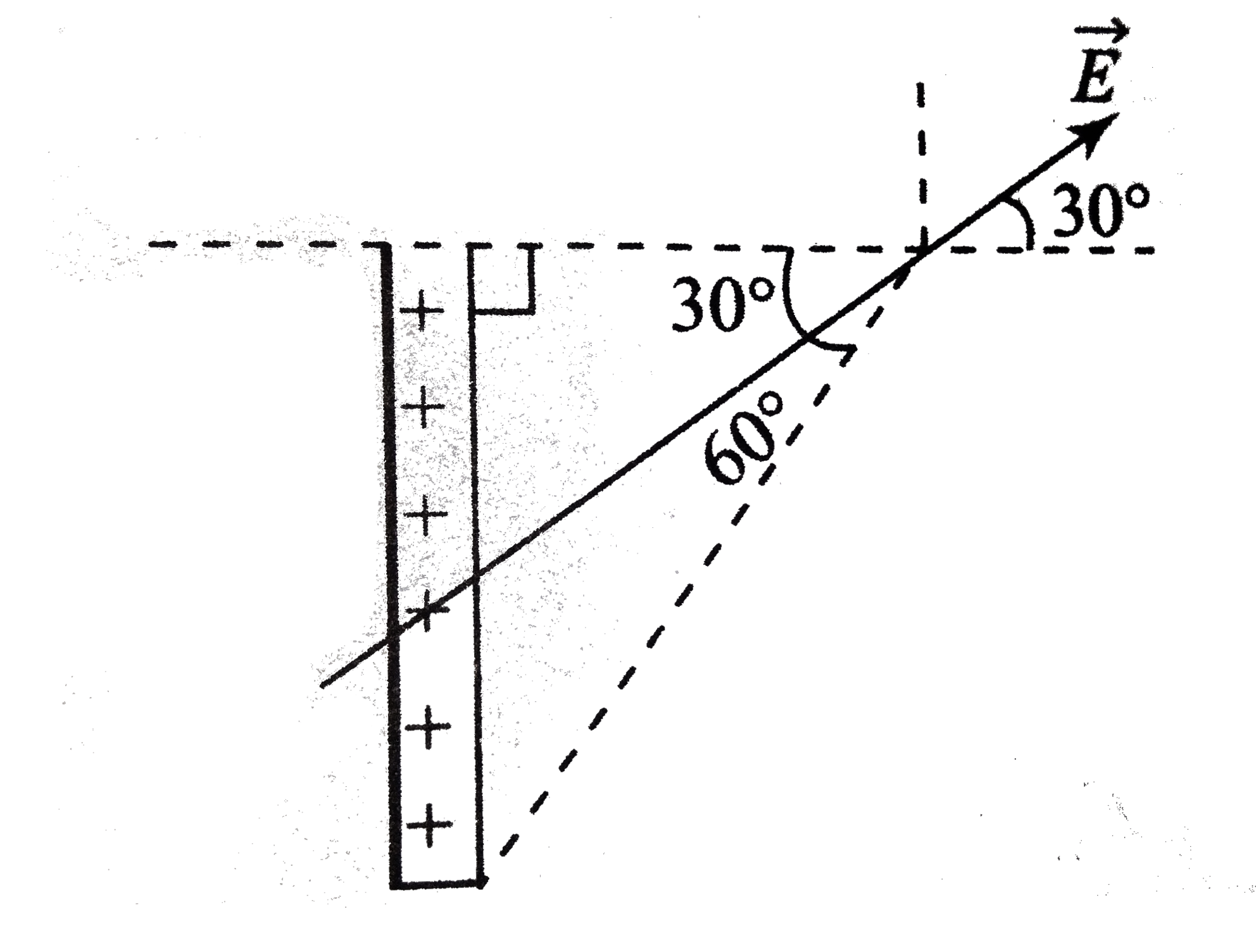
Topper's Solved these Questions
- COULOMB LAW AND ELECTRIC FIELDBook:CENGAGE PHYSICSChapter:COULOMB LAW AND ELECTRIC FIELDExercise:Multiple Correct
Explore 8 Videos
- COULOMB LAW AND ELECTRIC FIELDBook:CENGAGE PHYSICSChapter:COULOMB LAW AND ELECTRIC FIELDExercise:Comprehension
Explore 25 Videos
- COULOMB LAW AND ELECTRIC FIELDBook:CENGAGE PHYSICSChapter:COULOMB LAW AND ELECTRIC FIELDExercise:Subjective
Explore 32 Videos
- COMMUNICATION SYSTEMBook:CENGAGE PHYSICSChapter:COMMUNICATION SYSTEMExercise:QUESTION BANK
Explore 19 Videos
- Current ElectricityBook:CENGAGE PHYSICSChapter:Current ElectricityExercise:QUESTION BANK
Explore 40 Videos
Similar Questions
Calculate electric field intensity at point P due to a thin positive uniformly charged rod . Point P is at perpendicular distance d from the rod . The lower and upper ends of the rod make the angles α and β as shown below .
View SolutionDerive an expression for electric intensity E due to a uniformly charged thin spherical shell at a point outside the shell.
View Solution
Knowledge Check
The electric field due to a uniformly charged sphere is maximum at :
Acentre of sphereBinside the surfaceCat the surfaceDat infinite distance from the centreThe electric field intensity at point near and outside the surface of a charged conductor of any shate is E1 the elecric field intensity due to uniformly charged conductor of any shape is E1 the electric field intensity due ot uniformly charged infinite thin plane sheet is E2 the relation between E1 and E2 is
A2E1=E2BE1=E2CE1=2E2DE1=4E1The electric field intensity at point near and outside the surface of a charged conductor of any shate is E1 the elecric field intensity due to uniformly charged conductor of any shape is E1 the electric field intensity due ot uniformly charged infinite thin plane sheet is E2 the relation between E1 and E2 is
A2E1=E2BE1=E2CE1=2E2DE1=4E1
Calculate the potential at a point on the perpendicular bisector of uniformly charged thin rod (linear density of charge =λ) of length 2l at a distance a from the centre of the rod.
View SolutionFind the electric field due to an uniformly charged arc, at the center 'c'.

View SolutionFind the electric field at a point P on the perpendicular bisector of a uniformly charged rod. The lengthof the rod is L, the charge on it is Q and the distance of P from the centre of the rod is a.
View SolutionFind : (i)Electric field intensity due to an infinitely long uniformly charged, straight conductor , at a perpendicular distance d from rod.
(ii)Electric field intensity at a point on perpendicular bisector of uniformly charged rod of length l and charge Q at a distance d from the centre of rod.
View SolutionThe maximum electric field at a point on the axis of a uniformly charged ring is E0. At how many points on the axis will the magnitude of the electric field be E0/2.
View Solution

