Monochramatic light is incident on the pLane interface AB between two media of refractive indices μ1 and μ2(μ2>μ1) at an angle of incidence theta as shown in figure. The angle theta is infinitesimally greater thannte critical angle for the two media so thast total internal reflection takes place. Now, if a transparent slab DEFG of uniform thickness and of refractive inde μ2 is introduced on theinterface (as shown in figure ) , show that for any value of μ2 all light will ultimately be reflected back into medium II.
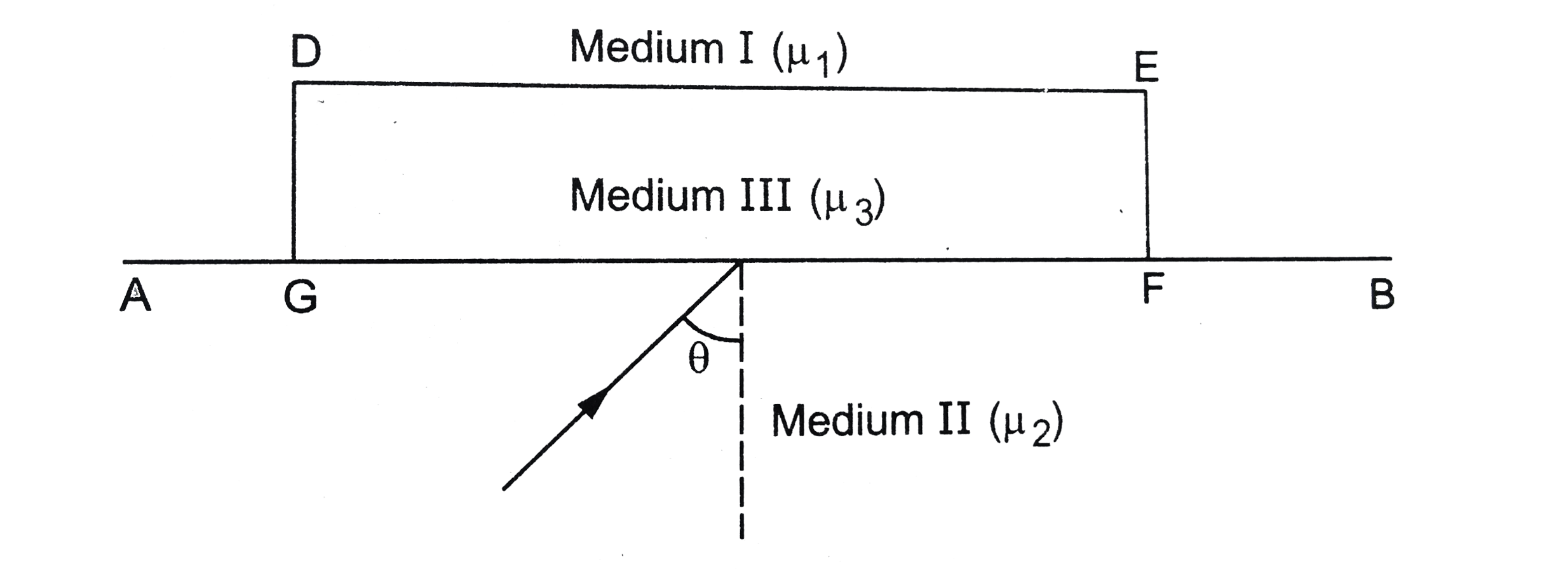
When the slab is not inserted,
θ≥C=sin−1(μ1μ2)∴sinθ>=μ1μ2 …(i)
When the slab is inserted, two cases arise.
(i) μ3≤μ1
We have sinθ≥μ1μ2≥μ3μ2
∴ light incident on AB at an angle greater than critical angle (sin−1μ3μ3) will suffer total internal reflection and go back to medium II.
(ii) μ3>μ1
sinθ≥μ1μ2<μ3μ2
As angle of incidence is less than critical angle, light entres into medium III. ltrgt Angle of refraction θ' is given by sinθsinθ'=μ3μ2
sinθ'=μ2μ3sinθ≥μ2μ3.μ1μ2
sinθ'≥μ1μ3
i.e., θ' is greater than critical angle. So total internal reflection occurs from face DE and the entire light is reflected back to medium II.
 .
.
Topper's Solved these Questions
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:Problem For Practice(c)
Explore 27 Videos
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:Problem For Practice(d)
Explore 35 Videos
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:Long Answer (a)
Explore 5 Videos
- PROPERTIES OF BULK MATTERBook:PRADEEPChapter:PROPERTIES OF BULK MATTERExercise:Multiple choice questions
Explore 7 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:Assertion- Reason Type questions
Explore 20 Videos
Similar Questions
A monochromatic light is incident on the plane interface AB between two media of refractive indices μ1 and (μ2>μ1) at an angle of incidence θ as shown in Fig.
The angle θ is infinitesimally greater than the critical angle for the two media so that total internal reflection takes place. Now, if a transparent slab DEFG of uniform thickness and of refractive index μ3 is introduced on the interface (as shown in the figure), show that for any value of μ3 all light will ultimately be reflected back into medium II.

View SolutionWhat is the relation between the refractive indicesμ,μ1 and μ2 if the behaviour of light rays is shown in Figure.
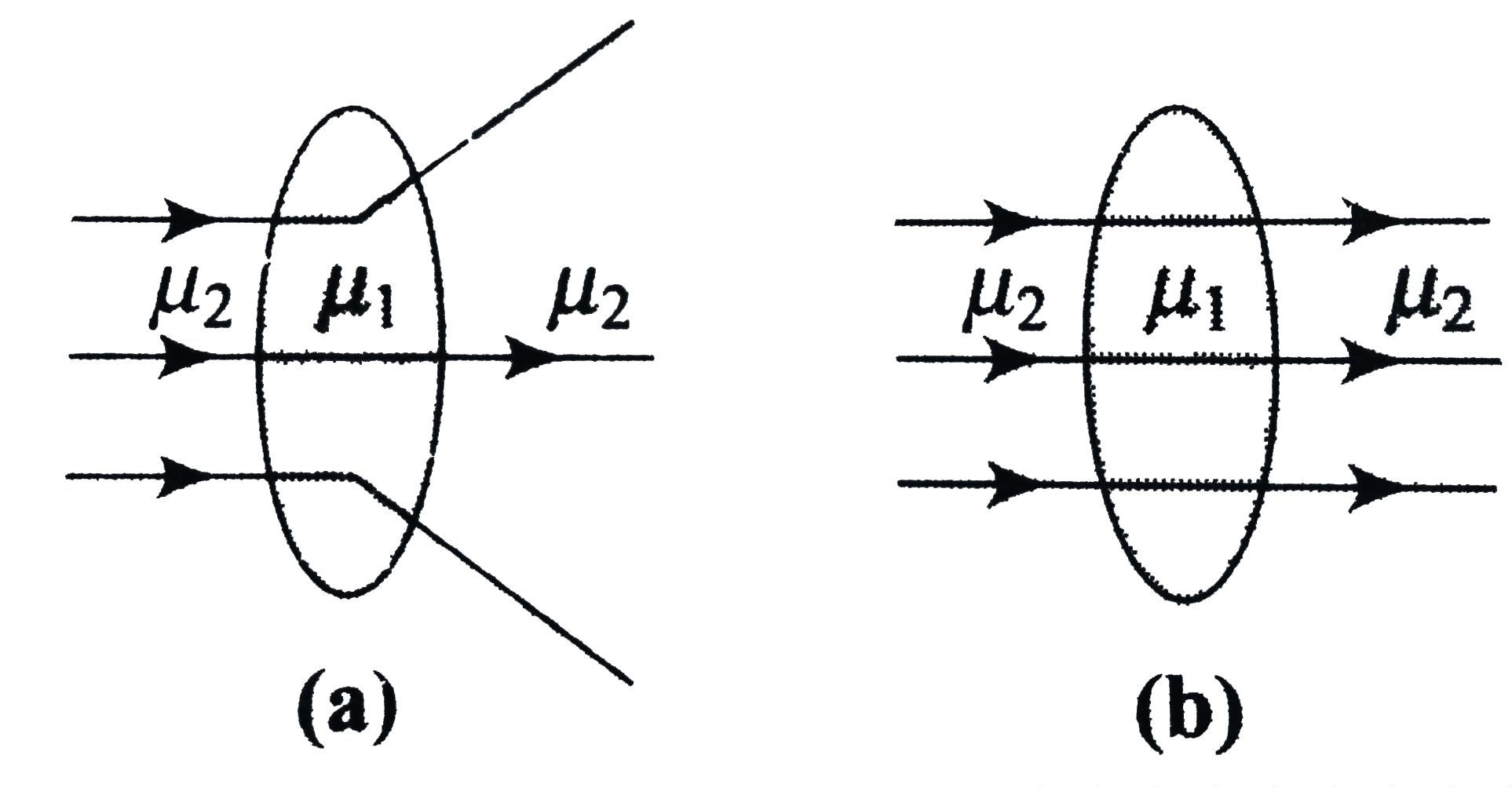
View Solution
Knowledge Check
The relation between refractive indices u,μ1,μ2. if the behaviour of light ray is as shown in figure
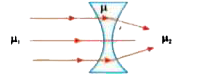 Aμ>μ1>μ2Bμ<μ2<μ1Cμ<μ2,μ=μ1Dμ2<μ1,μ=μ2
Aμ>μ1>μ2Bμ<μ2<μ1Cμ<μ2,μ=μ1Dμ2<μ1,μ=μ2Two optical media of refractive indices μ1 and μ2 contain x and y waves of same colour in the same thickness. Their refractive indices ratio is equal to
A(x−y)xB(x+y)xCxy−xDyxTwo optical media of refractive indices μ1 and μ2 contain x and y waves of same colour in the same thickness. Their refractive indices ratio is equal to
Ax−yxB(x+Y)xCxy−xDyx
A light ray is incident on a glass sphere of reflective index μ=√3 at an angle of incidence 60∘ as shown in Fig. Find the angles r, r′ e and the total deviation after two refractions.
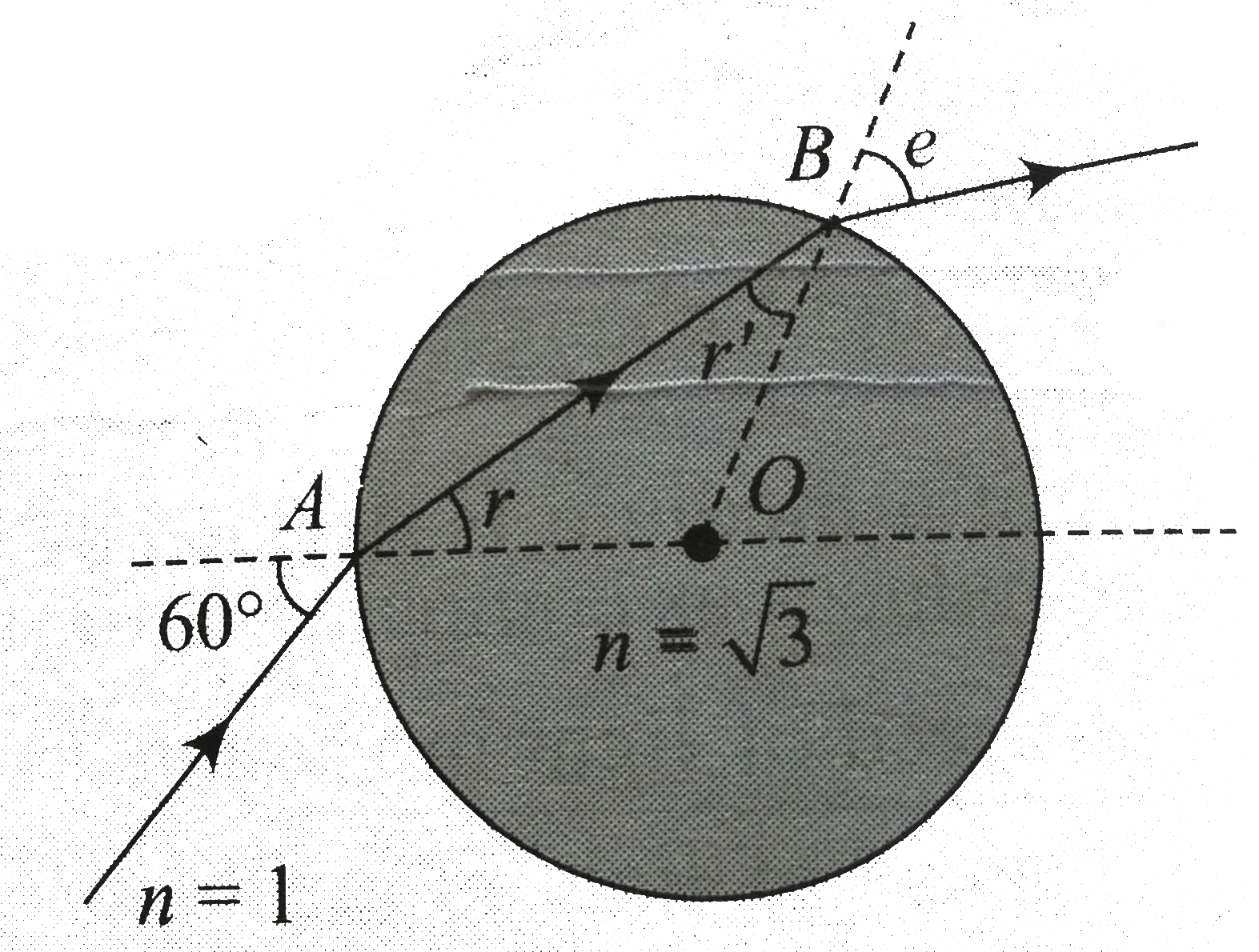
View SolutionFor total internal reflection to take place, the angle of incidence I and the refractive index μ of the medium must satisfy the inequality
View SolutionFor total internal reflection to take place, the angle of incidence i and the refractive index μ of the medium must satisfy the inequality
View SolutionIn total internal reflection when the angle of incidence is equal to the critical angle for the pair of media in contact, what will be angle of refraction?
View SolutionThe diagram shows a spherical surface which separates two media of refractive index, μ1andμ2. Respectively. Now, a point object is placed on the principal axis as shown in the figure. Then
View Solution

