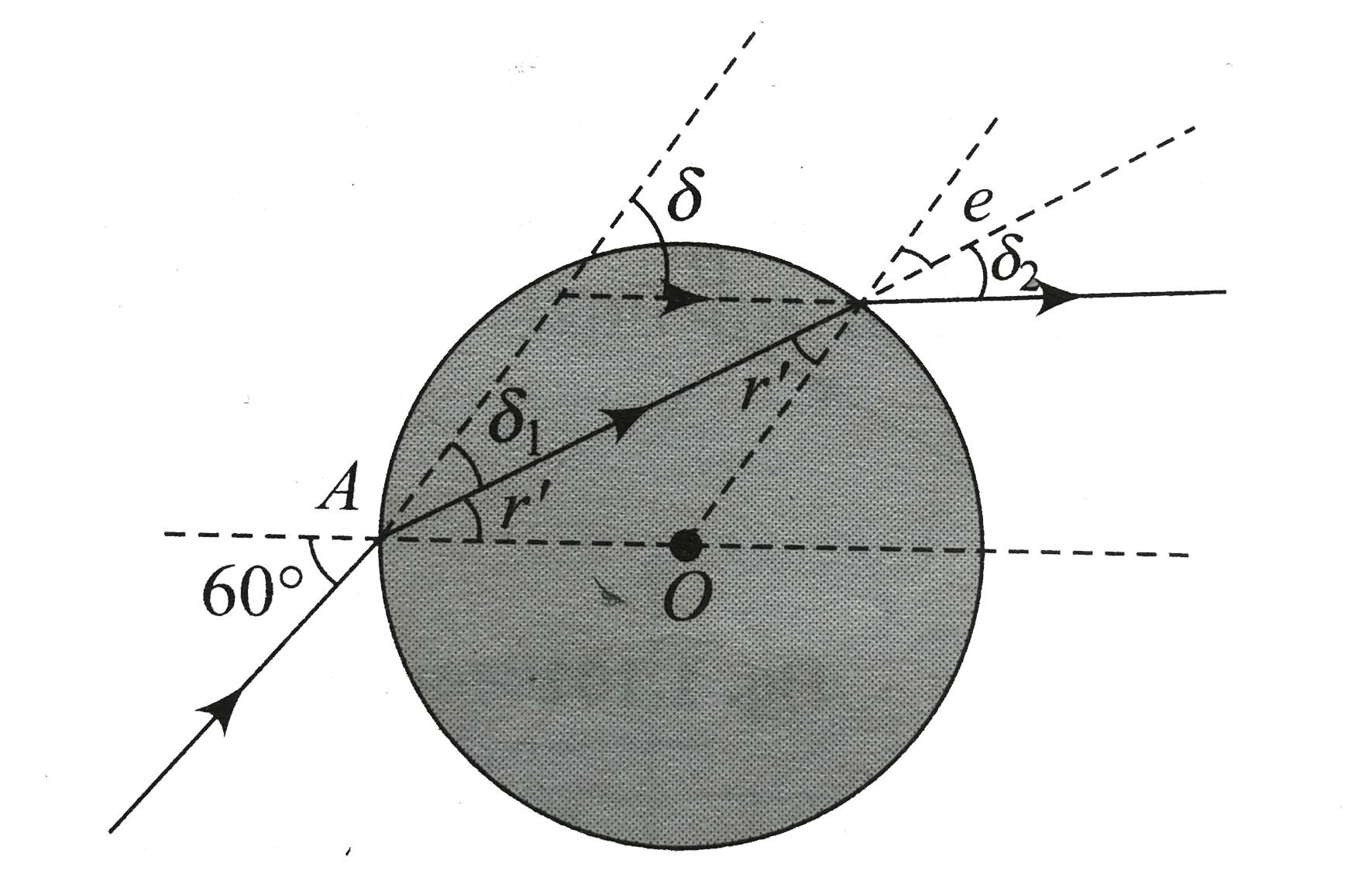
A light ray is incident on a glass sphere of reflective index μ=√3 at an angle of incidence 60∘ as shown in Fig. Find the angles r, r′ e and the total deviation after two refractions.
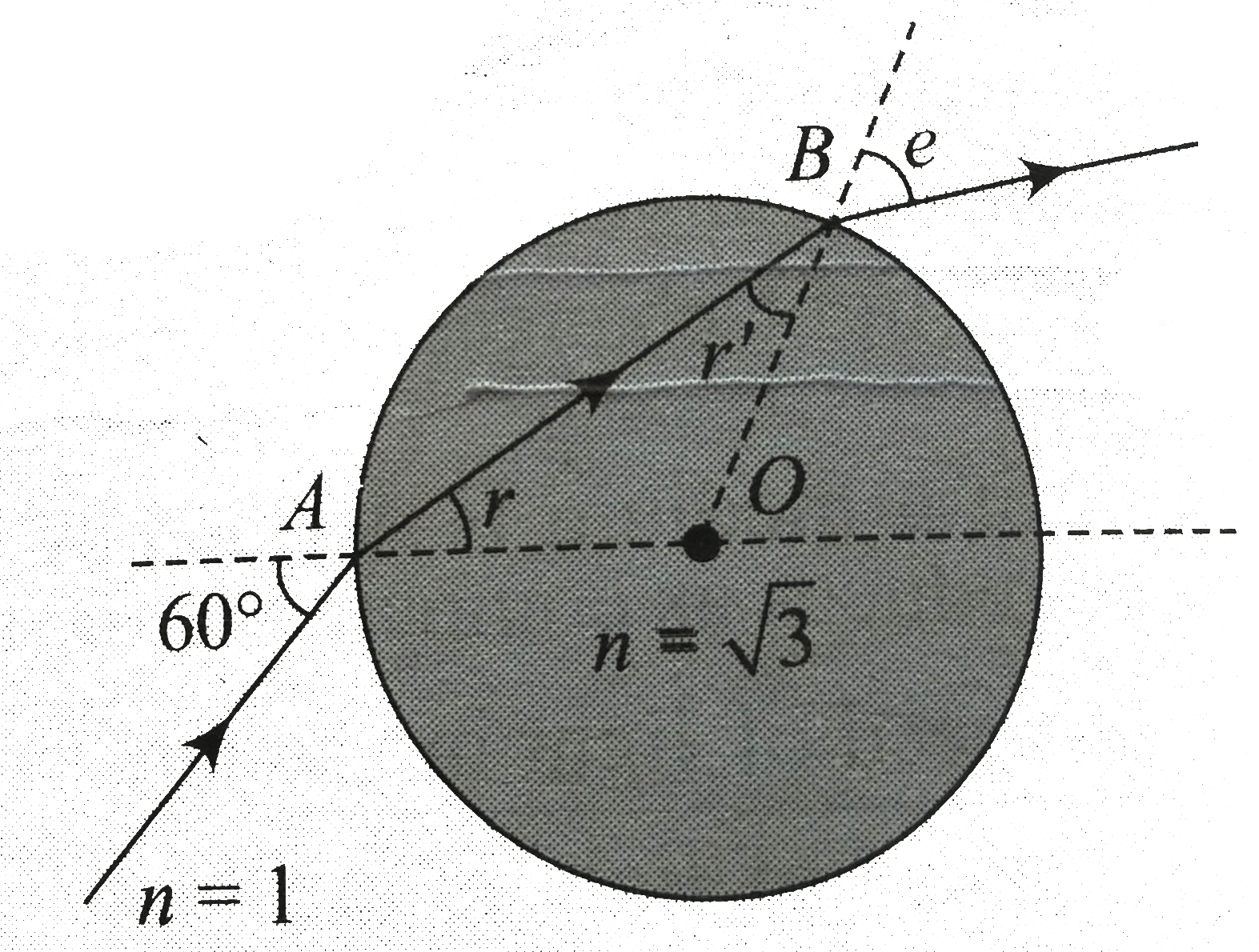
At point 'A' : Applying Snell's law
1sin60∘=√3sinr⇒r=30∘
From symmetry r′=r=30∘.
Again applying Snell's law at second surface (at poing 'B')
1sine=√3sinr.
⇒e=60∘
Deviation at the first surface, δ1=i−r=60∘−30∘=30∘
Deviation at the second surface, δ2=e−r′=60∘−30∘=30∘
Therefore, total deviation = 60∘.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Solved Examples
15 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise1.1
14 Videos
- FRICTIONBOOK - CENGAGE PHYSICSCHAPTER - FRICTIONEXERCISE - QUESTION BANK
1 Video
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Question Bank
39 Videos
Similar Questions
A light ray is incident on a glass sphere at an angle of incidence 60∘ as shown. Find the angles r, r', e and the total deviation after two refractions.

View SolutionA light ray is incident on a glass sphere at an angle of incidence 60∘ as shown. Find the angles r,f1,e and the total deviation after two refractions.

View Solution
Knowledge Check
A light ray is incident on a transparent sphere of index = √2 , at an angle of incidence =45∘ , What is the deviation of a tiny fraction of the ray, which enters the sphere, undergoes two internal reflections and then refracts out into air?
A270∘B240∘C120∘D180∘Light ray is incident on a prism of angle A=60∘and refractive indexμ=√2.the angle of incidence at which the emergent ray grazes the surface is given by
Asin−1(√3−12)Bsin−1(1−√32)Csin−1(√32)Dsin−1(2√3)A ray of light is incident on a glass slab of refractive index 1.5, making an angle of 40∘ with the surface. The angle of refraction in glass is
A40∘B30∘42'C50∘D60∘
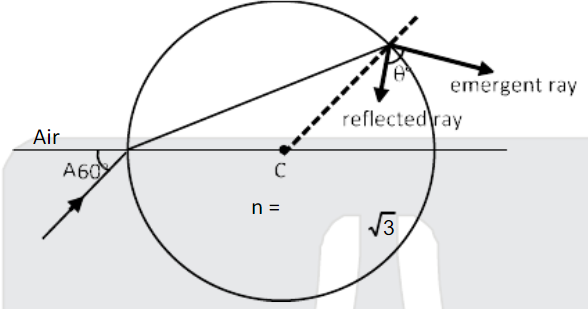
Light incidence on a sphere of refractive index √3 placed in a air as shown in Figure. Find the angle (θ)in degree between emergent ray and reflected ray.
View SolutionA light ray from air is incident on a glass plate of thickness t and refractive index μat an angle of incidence equal to the angle of total internal reflection of glass. Compute the displacement of the ray due to this plate in terms of thickness and refractive index of glass μ.
View SolutionA light ray is incident on a plane glass slab of thickness ‘t’ at an angle of incidence ‘i’ as shown in the figure. If μ is the refractive index of glass. Then find time taken by the light ray to travel through the slab.
View SolutionA ray of light is incident on a transparent plate of a material of refractive index √3 at the polarising angle. Find the angle of refraction.
View SolutionA ray of light strikes a transparent rectangular slab of refractive index √2 at an angle of incidence of 45∘. The angle between the reflected and refracted rays is
View Solution