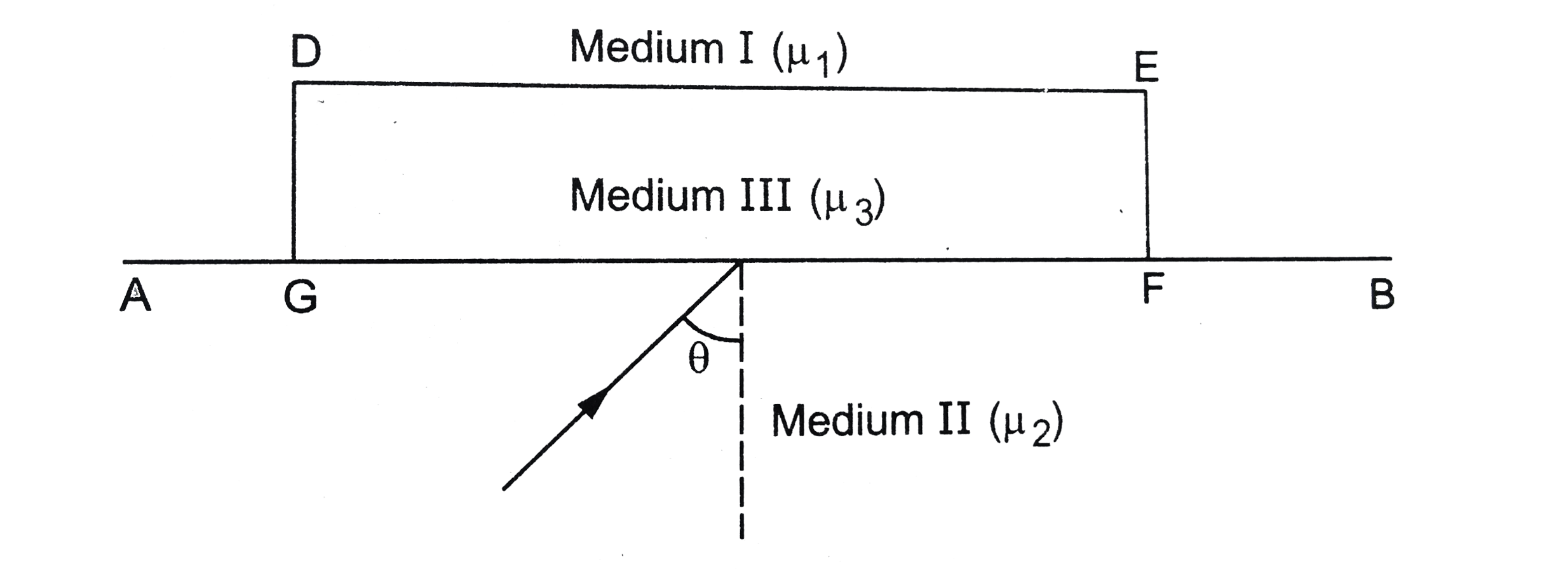
A monochromatic light is incident on the plane interface AB between two media of refractive indices μ1 and (μ2>μ1) at an angle of incidence θ as shown in Fig.
The angle θ is infinitesimally greater than the critical angle for the two media so that total internal reflection takes place. Now, if a transparent slab DEFG of uniform thickness and of refractive index μ3 is introduced on the interface (as shown in the figure), show that for any value of μ3 all light will ultimately be reflected back into medium II.

We will use the symbol ≤ to mean 'infinitesimally greater than'.
When the slab is not inserted,
θ≤θc=sin−1(μ1/μ2) or sinθ≥μ1/μ2
When the slab is inserted, we have two cases
μ3≤μ1 and μ3>μ1.
Case I. μ3<μ1 . We have sinθ≥μ1/μ2≥μ3/μ2
Thus, the light is incident on AB at an angle greater than the critical angle sin−1(μ3/μ2). It suffers total internal reflection and goes back to medium II.
Case II. μ3>μ1
sinθ≥μ1/μ2<μ3/μ2
Thus, the angle of incidence θ may be smaller than the critical angle sin−1(μ3/μ2) and hence it may enter medium III. The angle of refraction θ is given by (figure).
sinθsinθ′=μ3μ2 (i)
⇒sinθ′=μ2μ3sinθ≤μ2μ3⋅μ1μ2
Thus, sinθ′≥μ1μ3⇒θ′≥sin−1(μ1μ3) (ii)
As the slab has parallel faces, the angle of refraction at the face FG is equal to the angle of incidence at the face DE. Equation (ii) shows that this angle is infinitesimally greater than the critical angle here. Hence, the light suffers total internal reflection and falls at the surface FG at an angle of incidence θ′. At this face, it will refract into medium II and teh angle or refraction will be θ as shown by Eq. (i). Thus, the total ligh energy is ultimately reflected back into medium II.

Topper's Solved these Questions
- GEOMETRICAL OPTICSBook:CENGAGE PHYSICSChapter:GEOMETRICAL OPTICSExercise:Solved Examples
Explore 15 Videos
- GEOMETRICAL OPTICSBook:CENGAGE PHYSICSChapter:GEOMETRICAL OPTICSExercise:Exercise1.1
Explore 14 Videos
- FRICTIONBook:CENGAGE PHYSICSChapter:FRICTIONExercise:QUESTION BANK
Explore 1 Video
- GRAVITATIONBook:CENGAGE PHYSICSChapter:GRAVITATIONExercise:Question Bank
Explore 39 Videos
Similar Questions
Monochramatic light is incident on the pane interface AB between two media of refractive indices μ1 and μ2(μ2>μ1) at an angle of incidence theta as shown in figure. The angle theta is infinitesimally greater thannte critical angle for the two media so thast total internal reflection takes place. Now, if a transparent slab DEFG of uniform thickness and of refractive inde μ2 is introduced on theinterface (as shown in figure ) , show that for any value of μ2 all light will ultimately be reflected back into medium II.
View SolutionA light ray is incident on a glass sphere of reflective index μ=√3 at an angle of incidence 60∘ as shown in Fig. Find the angles r, r′ e and the total deviation after two refractions.
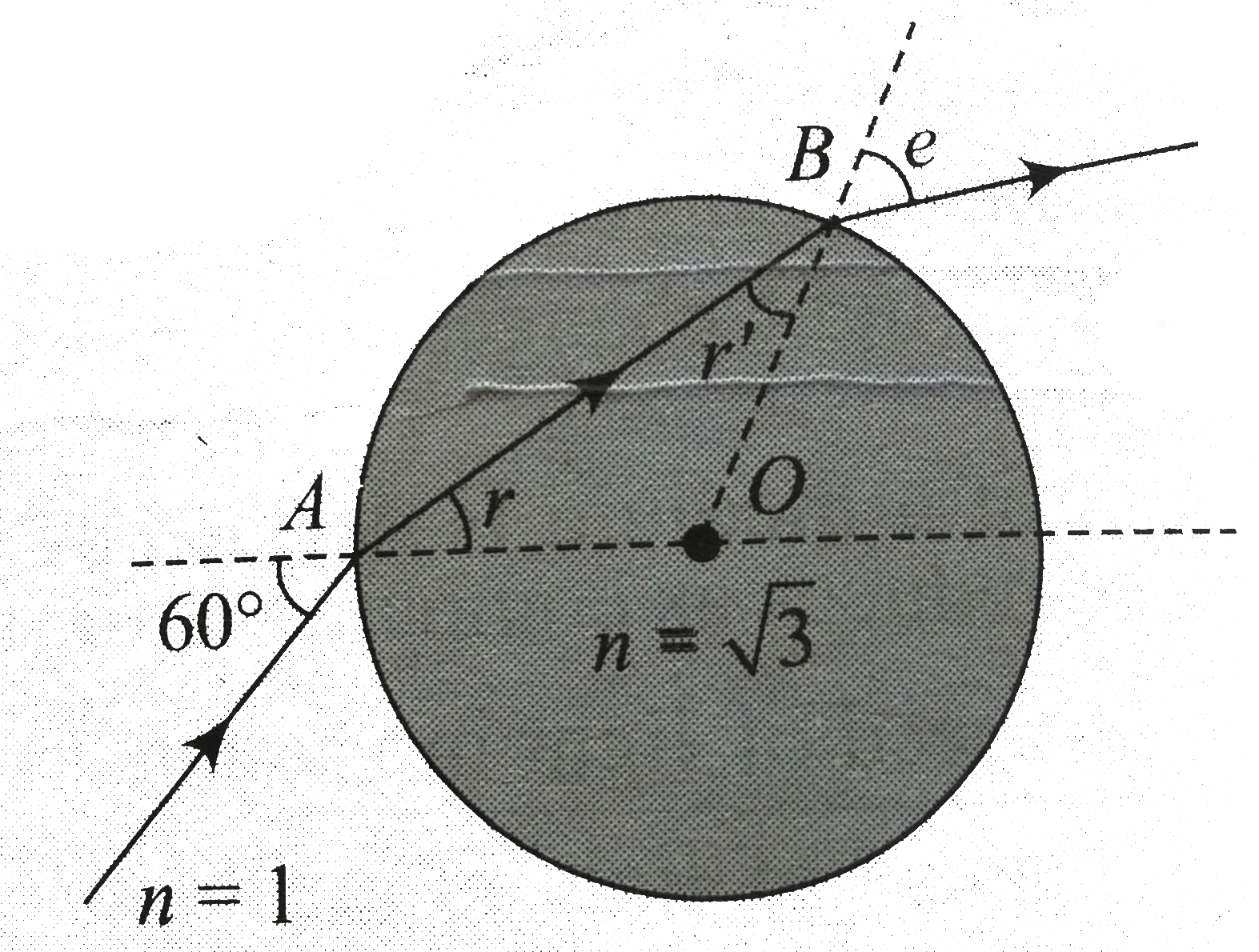
View Solution
Knowledge Check

A ray is incident on interface of two media at critical angle as shown in the figure.Aif μ1 and μ2 both are increased by same amount the ray will suffer total internal reflection.Bif μ1 and μ2 both are increased by same amount the ray will suffer refraction and angle of refraction will be less then 90∘Cif μ1 and μ2 both are doubled ray will suffer total internal reflection.Dif μ1 ad μ2 both are doulbed ray will suffer refraction and angle of refraction will be less te 90∘In total internal reflection when the angle of incidence is equal to the critical angle for the pair of media in contact, what will be angle of refraction?
A180∘B0∘CEqual to angle of incidenceD90∘Two optical media of refractive indices μ1 and μ2 contain x and y waves of same colour in the same thickness. Their refractive indices ratio is equal to
A(x−y)xB(x+y)xCxy−xDyx
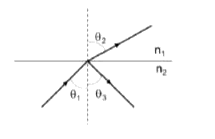
A monochromatic beam of light is incident at the interface of two materials of refractive index n1 and n2 as shown . If n1>n2 and θC is the critical angle then which of the following statements is NOT true ?
View SolutionTwo optical media of refractive indices μ1 and μ2 contain x and y waves of same colour in the same thickness. Their refractive indices ratio is equal to
View SolutionFor total internal reflection to take place, the angle of incidence I and the refractive index μ of the medium must satisfy the inequality
View SolutionFor total internal reflection to take place, the angle of incidence i and the refractive index μ of the medium must satisfy the inequality
View SolutionIf a ray of light takes t1 and t2 times in two media of absolute refractive indices μ1 and μ2 respectively to travel same distance, then
View Solution
