For total internal reflection to take place, the angle of incidence i and the refractive index μ of the medium must satisfy the inequality
1sini<μ
1sini>μ
sini<μ
sini>μ
The correct Answer is:A
For total internal reflection I<C
⇒sin>sinC⇒sini>1μ⇒1sini<μ.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - A2ZCHAPTER - GEOMETRICAL OPTICSEXERCISE - Refraction At Curved Surface
64 Videos
- GEOMETRICAL OPTICSBOOK - A2ZCHAPTER - GEOMETRICAL OPTICSEXERCISE - Prism Theory And Dispersion Of Light
45 Videos
- ELECTROMAGNETIC WAVES AND COMMUNICATION SYSTEM BOOK - A2ZCHAPTER - ELECTROMAGNETIC WAVES AND COMMUNICATION SYSTEM EXERCISE - Section D - Chapter End Test
30 Videos
- MAGNETISM AND MATTERBOOK - A2ZCHAPTER - MAGNETISM AND MATTEREXERCISE - Section D - Chapter End Test
30 Videos
Similar Questions
The path of a ray of light passing through an equilateral glass prism ABC is shown in figure. The ray of light is incident on face BC at the critical angle for just total internal reflection. The total internal reflection. The total angle of deviation after the refraction at face AC is 108∘. Calculate the refractive index of the glass.
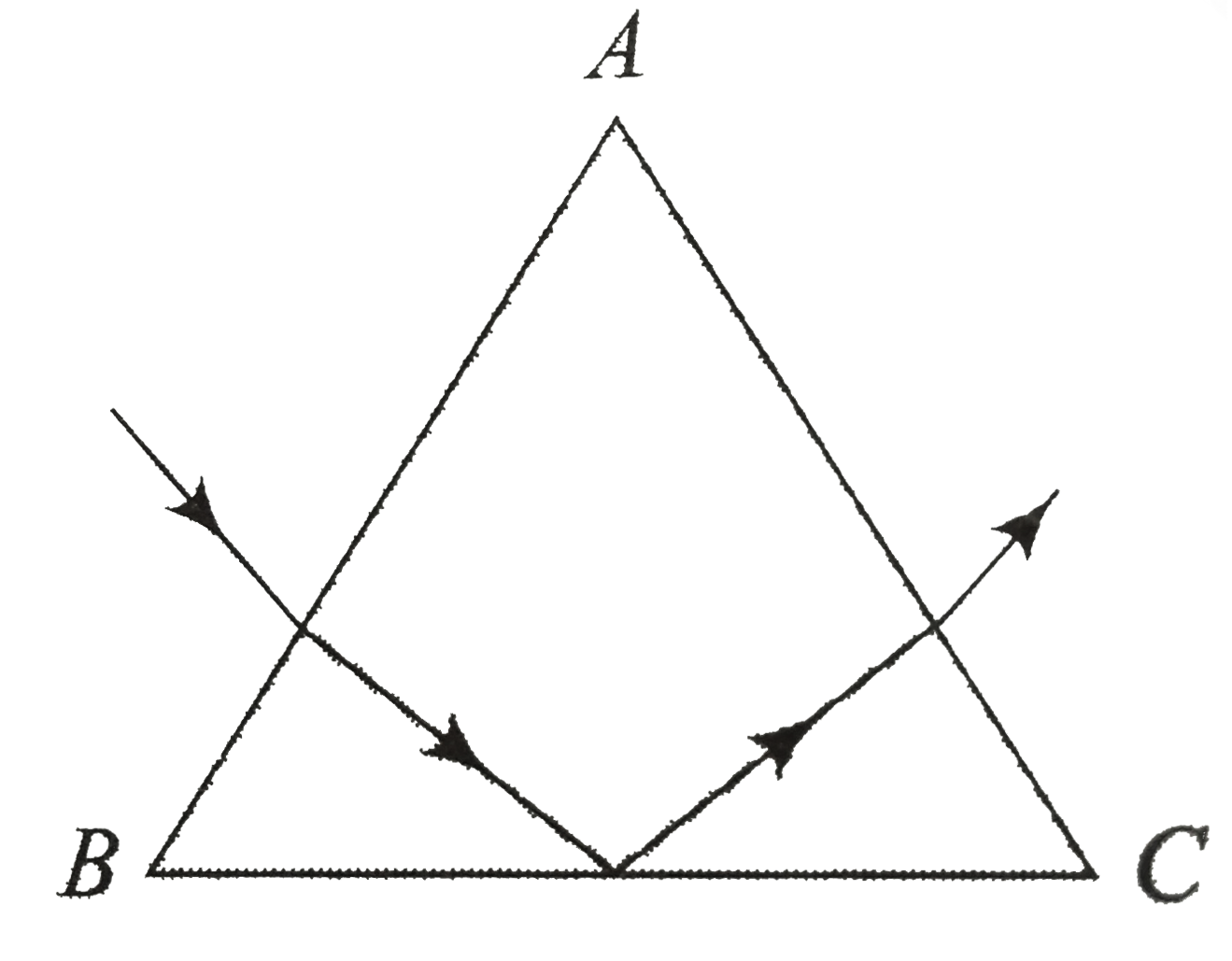
View SolutionAt what angle should a ray of light be incident on the face of a prism of refracting angle 60° so that it just suffers total internal reflection at the other face ? The refractive index of the material of the prism is 1.524.
View Solution
Knowledge Check
In total internal reflection when the angle of incidence is equal to the critical angle for the pair of medium in contact, what will be angle of refraction? In total internal reflection when the angle of incidence is equal to the critical angle for the pair of medium in contact, what will be angle of refraction? In total internal reflection when the angle of incidence is equal to the critical angle for the pair of medium in contact, what will be angle of refraction?
A90∘B180∘C0∘Dequal to angle of incidenceIn total internal reflection when the angle of incidence is equal to the critical angle for the pair of media in contact, what will be angle of refraction?
A180∘B0∘CEqual to angle of incidenceD90∘Light travelling through three transparent substances follows the path shown in the figure. Assuming that total internal reflection does take place on the bottom surface of medium 2, arrange the refractive index in the increasing order.
 Aμ1<μ2<μ3Bμ2<μ1<μ3Cμ1<μ3<μ3Dμ3<μ1<μ2
Aμ1<μ2<μ3Bμ2<μ1<μ3Cμ1<μ3<μ3Dμ3<μ1<μ2
When a light ray centers a refracing medium, it is found that the magnitude of the angle of refraction is equal to half the angle of reflection. If μ is the refractive index of the medium, then the angle of incidence is
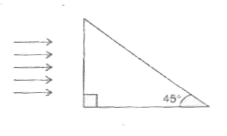
View SolutionPreferential filtering of light consisting of different wavelengths can be done using total internal reflection. The concept of filtering lies in the fact that different wavelengths have different refractive indices in a medium The beam of light with different wavelengths are made incident on an isosceles right angled prism as shown in the figure. The wavelength or wavelengths which satisfy the condition of totai internal reflection, θsin≥(1μ), get reflected
Others get refracted, hence gets separated. G is the angle of incidence and u. is the refractive index .of the particular wavelength in that particular medium. Thus, by changing the medium and by changing the angles of the prism we can satisfy the condition df total internal reflection for a particular wavelength, which gets separated out.
Q An experiment was performed based on the above theory with red, green and blue light. Their refractive indices in the material were 1.39, 1.44 and 1.47, respectively. Which colour would get separated?
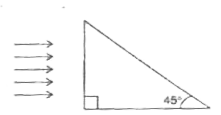
View SolutionPreferential filtering of light consisting of different wavelengths can be done using total internal reflection. The concept of filtering lies in the fact that different wavelengths have different refractive indices in a medium The beam of light with different wavelengths are made incident on an isosceles right angled prism as shown in the figure. The wavelength or wavelengths which satisfy the condition of totai internal reflection, θsin≥(1μ), get reflected
Others get refracted, hence gets separated. G is the angle of incidence and u. is the refractive index .of the particular wavelength in that particular medium. Thus, by changing the medium and by changing the angles of the prism we can satisfy the condition df total internal reflection for a particular wavelength, which gets separated out.
Q Now instead of changing the material of prism, we change one of the angle of prism to 300 Then, which of the colour gets separated?
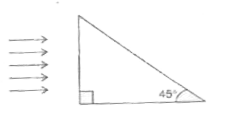

View SolutionPreferential filtering of light consisting of different wavelengths can be done using total internal reflection. The concept of filtering lies in the fact that different wavelengths have different refractive indices in a medium The beam of light with different wavelengths are made incident on an isosceles right angled prism as shown in the figure. The wavelength or wavelengths which satisfy the condition of totai internal reflection, θsin≥(1μ), get reflected
Others get refracted, hence gets separated. G is the angle of incidence and u. is the refractive index .of the particular wavelength in that particular medium. Thus, by changing the medium and by changing the angles of the prism we can satisfy the condition df total internal reflection for a particular wavelength, which gets separated out.
Q If hypothetically the density of the material is increased gradually, then which of the colour gets separated next?
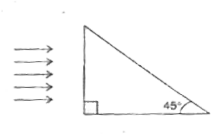
View SolutionPreferential filtering of light consisting of different wavelengths can be done using total internal reflection. The concept of filtering lies in the fact that different wavelengths have different refractive indices in a medium The beam of light with different wavelengths are made incident on an isosceles right angled prism as shown in the figure. The wavelength or wavelengths which satisfy the condition of totai internal reflection, θsin≥(1μ), get reflected
Others get refracted, hence gets separated. G is the angle of incidence and u. is the refractive index .of the particular wavelength in that particular medium. Thus, by changing the medium and by changing the angles of the prism we can satisfy the condition df total internal reflection for a particular wavelength, which gets separated out.
Q As the density of the material-of the prism keeps on increasing, then which of the following statement holds good
View Solution
