The path of a ray of light passing through an equilateral glass prism ABC is shown in figure. The ray of light is incident on face BC at the critical angle for just total internal reflection. The total internal reflection. The total angle of deviation after the refraction at face AC is 108∘. Calculate the refractive index of the glass.
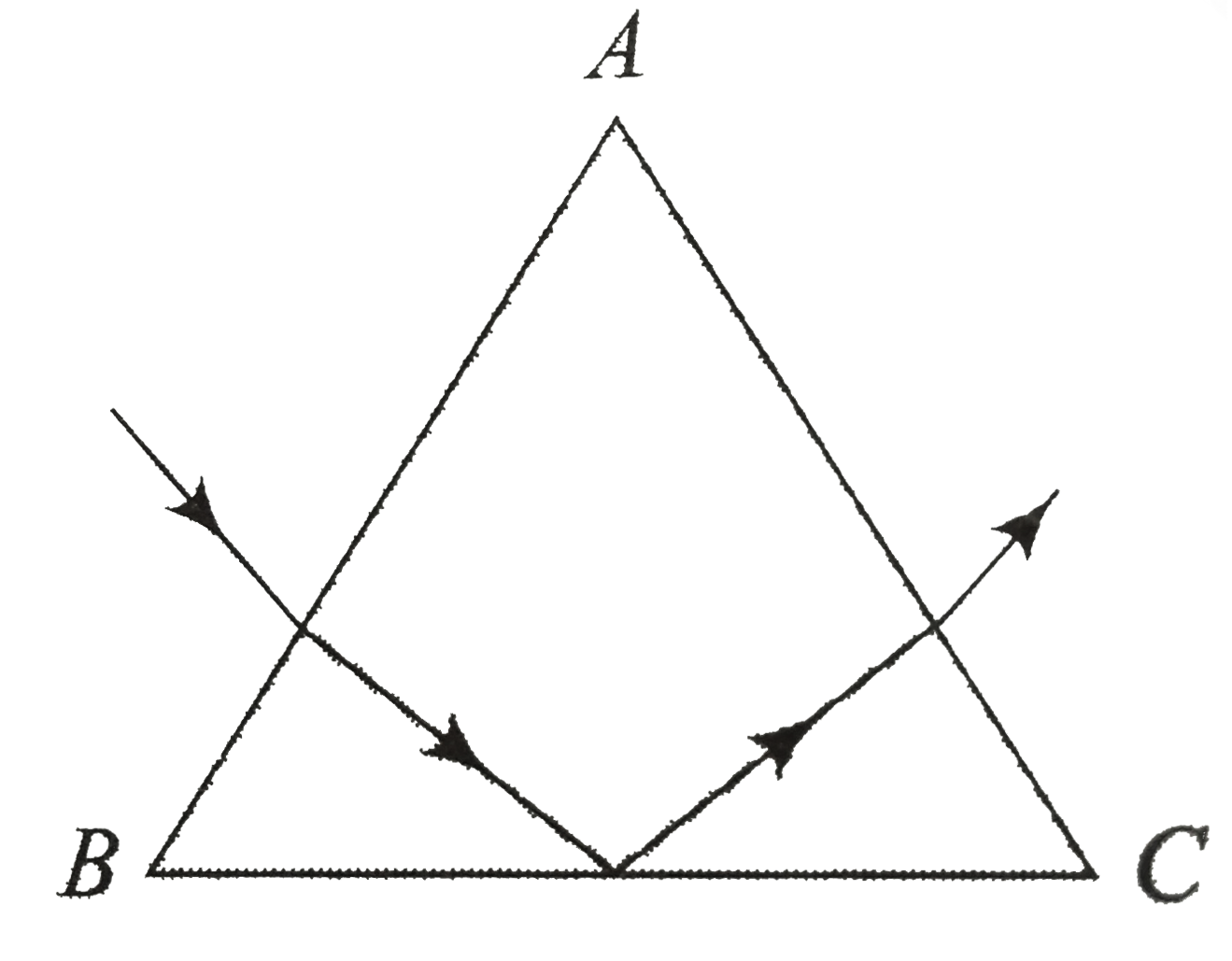
In the figure shown,
r2=C
r1=60−r2=60−C
r3=60−r2=60−C
r1=r3=r (say)
i1=i2=i (say)
Net deviation, δ=(1−r)+(180−2r2)+(i−r)=108∘
r2=r−i=36∘
C+60−C−i=36∘
i=24∘,sin24∘≈0.40
Form Snell's law, we have
sin24∘=μsinr
0.4=μsin(60∘−C)
0.4=μ[√32cosC−12μ]
0.8=√3μ√1−1μ2−1
∴μ2−1=1.08
μ=1.447
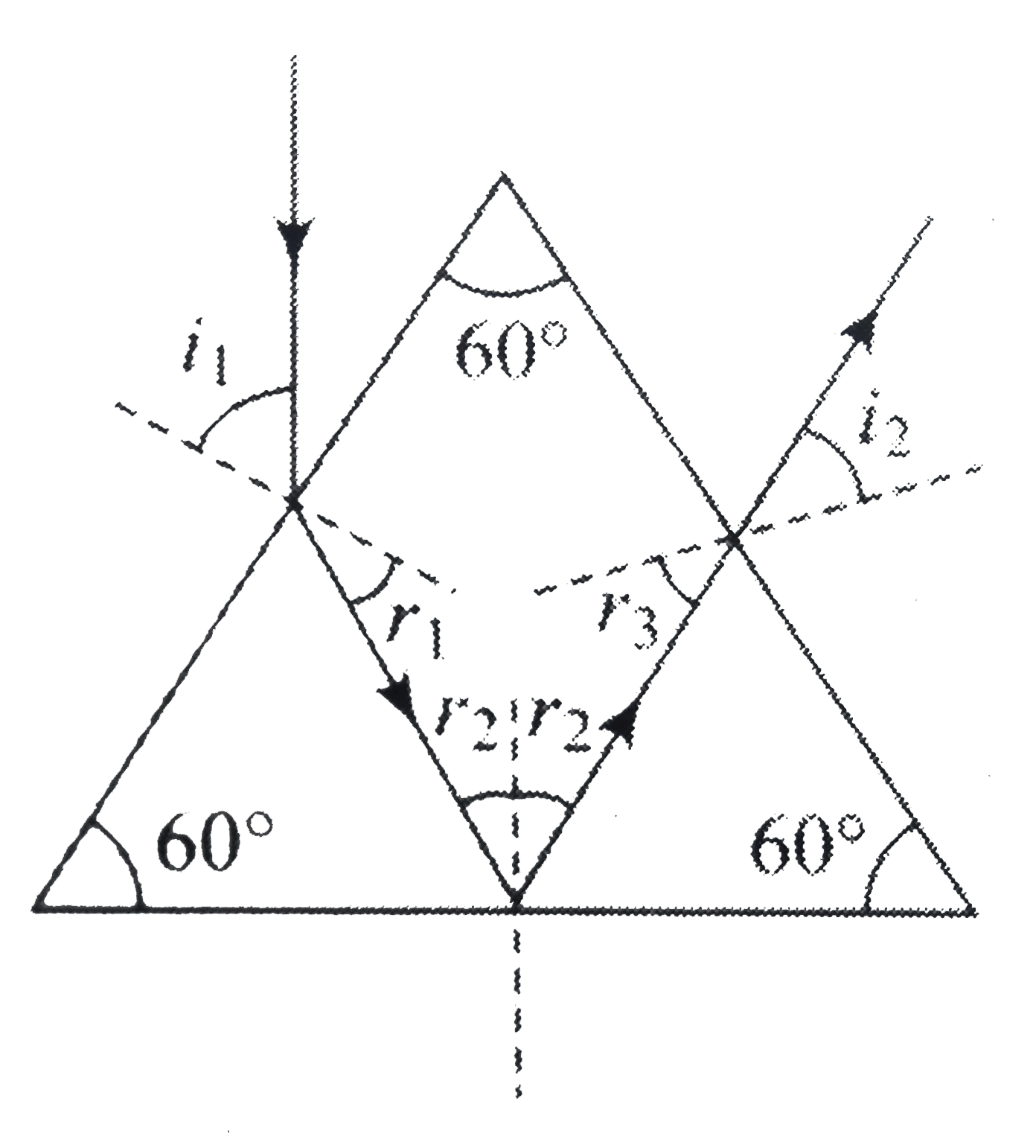
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise1.5
22 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise1.6
15 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise1.3
25 Videos
- FRICTIONBOOK - CENGAGE PHYSICSCHAPTER - FRICTIONEXERCISE - QUESTION BANK
1 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Question Bank
39 Videos
Similar Questions
A ray of light passes through a right angled prism as shown in the figure. State the angle of incidence at the faces AC and BC.
View SolutionA ray of light passes through an equilateral glass prism in such a way that the angle of incidence is equal to the angle of emergence and each of these angles is 34 times the angle of the prism. Determine the angle of deviation and the refractive index of the glass prism.
View Solution
Knowledge Check
A ray of light incident on a transparent sphere at an angle π/4 and refracted at an angle r, emerges from the sphere after suffering one internal reflection. The total angle of deviation of the ray is
A3π2−4rBπ2−4rCπ4−rD5π2−4rThe critical angle for total internal reflection is_________ when a ray of light travels from glass to water than when it travels from glass to air.
AequalBlesserCgreaterDnone of theseA ray of light incident on a glass sphere (refractive index √3 ) suffers total internal reflection before emerging out exactly parallel to the incident ray. The angle of incidence was
A75∘B30∘C45∘D60∘
At what angle should a ray of light be incident on the face of a prism of refracting angle 60∘ so that it just suffers total internal reflection at the other face ? The refractive index of the prism is 1.524.
View SolutionThe figure shows the path of a ray passing through an equiangular prism PQR. It is incident on face PR at angle slightly greater than the critical angle for total internal reflection . If the angle α shown in the figure is 30∘ . Calculate the R.I. of the material of the prism.
_E01_145_Q01.png)
View SolutionAt what angle should a ray of light be incident on the face of a prism of refracting angle 60° so that it just suffers total internal reflection at the other face ? The refractive index of the material of the prism is 1.524.
View SolutionAt what angle should a ray of light be incident on the face of a prism of refracting angle 60∘, so that it just suffers total internal reflection at the other face ? The refractive index of the prism is 1.524.
View SolutionThe angle of incidence for a ray of light passing through an equilateral glass prism is equal to its angle of emergence. Also, the angle of emergence is 3/4 times the angle of prism. Calculate the angle of deviation and refractive index of prism's material.
View Solution
