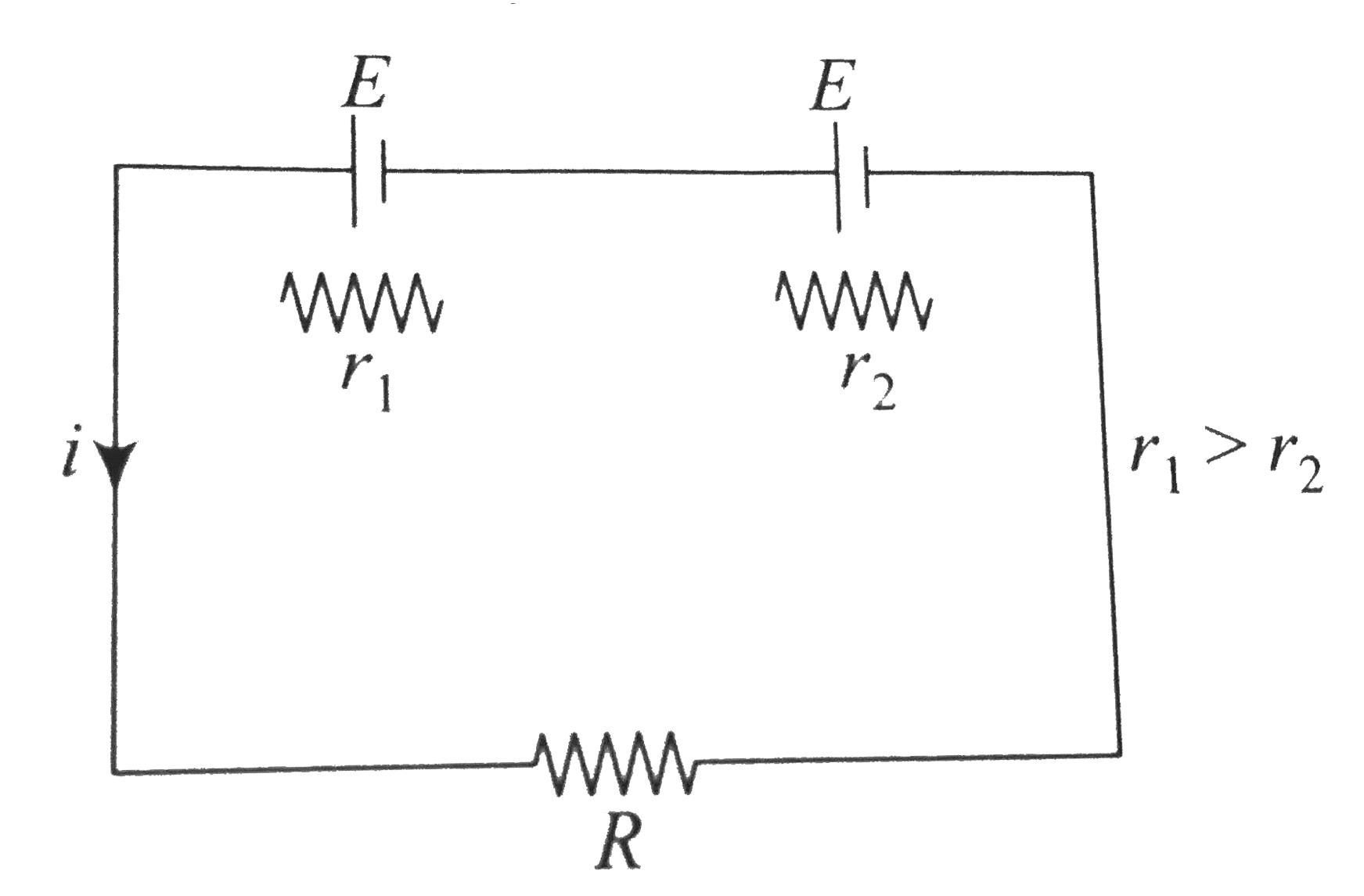
Two cells, having the same emf, are connected in series through an external resistance $R$ . Cells have internal resistance $r_{1}$ and $r_{2} (r_{1} > r_{2})$ respectively. When the circuit is closed, the potentail difference across the first cell is zero the value of $R$ is

$r_{1} - r_{2}$

$\frac{r_{1} + r_{2}}{2}$

$\frac{r_{1} - r_{2}}{2}$

$r_{1} + r_{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Updated on:21/07/2023

Two cells, having the same emf, are connected in series through an external resistance $R$ . Cells have internal resistance $r_{1}$ and $r_{2} (r_{1} > r_{2})$ respectively. When the circuit is closed, the potentail difference across the first cell is zero the value of $R$ is
A $r_{1} + r_{2}$
B $r_{1} - r_{2}$
C $\frac{r_{1} + r_{2}}{2}$
D $\frac{r_{1} - r_{2}}{2}$
Two cells, having the same emf, are connected in series through an external resistance $R$ . Cells have internal resistance $r_{1}$ and $r_{2} (r_{1} > r_{2})$ respectively. When the circuit is closed, the potentail difference across the first cell is zero the value of $R$ is
A $R_{1} - R_{2}$
B $\frac{R_{1} + R_{2}}{2}$
C $\frac{R_{1} - R_{2}}{2}$
D $R_{1} + R_{2}$
Two cells of emf 3V and 5V and internal resistance $r_{1}$ and $r_{2}$ respectively are in series with an external resistance R. if the p.d. across 1 st cell is zero, then R is
A $\frac{5 r_{1} - 3 r_{2}}{3}$
B $\frac{2 r_{1} - 3 r_{2}}{4}$
C $\frac{3 r_{1} - 5 r_{2}}{3}$
D $\frac{4 r_{1} - 5 r_{2}}{3}$