A cell of e.m.f. E is connected with an external resistance R , then p.d. across cell is V . The internal resistance of cell will be
The correct Answer is:B
To find the internal resistance of the cell, we can use the relationship between the electromotive force (e.m.f.) of the cell, the potential difference (p.d.) across the cell, the external resistance, and the internal resistance. Here’s a step-by-step solution:
Step 1: Understand the relationship between e.m.f., p.d., and resistances
The e.m.f. (E) of the cell is the maximum potential difference when no current is flowing. When the cell is connected to an external resistance (R), the potential difference (V) across the terminals of the cell decreases due to the internal resistance (r) of the cell.
Step 2: Write the equation for the circuit
According to Kirchhoff's voltage law, the sum of the potential differences in a closed circuit is equal to zero. Therefore, we can write:
E=V+I⋅r
Where:
- E = e.m.f. of the cell
- V = potential difference across the cell
- I = current flowing through the circuit
- r = internal resistance of the cell
Step 3: Express the current (I)
The current I can be expressed using Ohm's law:
I=VR
Where R is the external resistance.
Step 4: Substitute the expression for I into the equation
Substituting I into the equation from Step 2 gives:
E=V+(VR)⋅r
Step 5: Rearrange the equation to solve for internal resistance (r)
Rearranging the equation:
E−V=VR⋅r
Now, multiply both sides by R:
R(E−V)=V⋅r
Now, divide both sides by V:
r=R(E−V)V
Final Answer
The internal resistance r of the cell is given by:
r=R(E−V)V
---
The e.m.f. (E) of the cell is the maximum potential difference when no current is flowing. When the cell is connected to an external resistance (R), the potential difference (V) across the terminals of the cell decreases due to the internal resistance (r) of the cell.
According to Kirchhoff's voltage law, the sum of the potential differences in a closed circuit is equal to zero. Therefore, we can write:
E=V+I⋅r
Where:
- E = e.m.f. of the cell
- V = potential difference across the cell
- I = current flowing through the circuit
- r = internal resistance of the cell
The current I can be expressed using Ohm's law:
I=VR
Where R is the external resistance.
Substituting I into the equation from Step 2 gives:
E=V+(VR)⋅r
Rearranging the equation:
E−V=VR⋅r
Now, multiply both sides by R:
R(E−V)=V⋅r
Now, divide both sides by V:
r=R(E−V)V
The internal resistance r of the cell is given by:
r=R(E−V)V
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:ERRORLESS Chapter:CURRENT ELECTRICITYExercise:Kirchhoff s Law, cells
Explore 8 Videos
- CURRENT ELECTRICITYBook:ERRORLESS Chapter:CURRENT ELECTRICITYExercise:Different Measuring Instruments
Explore 1 Video
- COMMUNICATION SYSTEMBook:ERRORLESS Chapter:COMMUNICATION SYSTEMExercise:S E T
Explore 14 Videos
- ELECTRO MAGNETIC INDUCTIONBook:ERRORLESS Chapter:ELECTRO MAGNETIC INDUCTIONExercise:SET
Explore 20 Videos
Similar Questions
When a celll is connected to an external resistance R1, current through it is i1. When the same cell is connected to an external resistance R2, current through it is i2. Calculate the emf and internal resisance of the cell.
View SolutionThe maximum power dissipated in an external resistance R, when connected to a cell of emf E and internal resistance r, will be
View Solution
Knowledge Check
A cell of emf 1.5 Vis connected with an external resistance 2Ω. The potential difference falls to 1.0 v. The internal resistance of cell is
A1.5ΩB1.0ΩC10.0ΩD2.0ΩA cell of emf 1.5 Vis connected with an external resistance 2Ω. The potential difference falls to 1.0 v. The internal resistance of cell is
A1.5ΩB1.0ΩC10.0ΩD2.0ΩA cell of emf 1.5 V is connected with an external resistance 20Ω. The potential difference falls to 1.0 V. The internal resistance of cell is
A1.5ΩB1.0ΩC10.0ΩD2.0Ω
The emf of a cell is 2 V. When the terminals of the cell is connected to a resistance 4Ω. The potential difference across the terminals, if internal resistance of cell is 1Ω is
View SolutionTwo cells of same emf ε but of different internal resistances r1 and r2 are connected in series with an external resistance R. The potential drop across the first cell is found to be zero. The external resistance R is
View SolutionTwo cells of the same e.mf. e but different internal resistances r1andr2 are connected in series with an external resistance 'R'. The potential drop across the first cell is found to be zero. The external resistance Ris

View SolutionTwo cells A and B of e.m.f.2 V and 1.5 V respectively, are connected as shown in figure through an external resistance 10 Ω The internal resistance of each cell is 5 Ω. The potential difference EAandEB across the terminals of the cells A and B respectively are
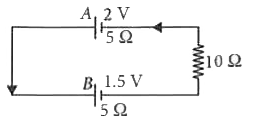
View SolutionIn a connection of 10 dry cells each of emf E and internal resistance r in series, two cell is connected opposite. Net emf and net internal resistance will be:
View Solution

