Force of attraction between the plates of a parallel plate capacitor is
q22ε0AK
q2ε0AK
q2ε0A
q22ε0A2K
The correct Answer is:A
To find the force of attraction between the plates of a parallel plate capacitor, we can follow these steps:
Step 1: Understand the Electric Field
The electric field (E) between the plates of a parallel plate capacitor can be derived from the charge on the plates. For a single plate with surface charge density σ, the electric field produced by that plate is given by:
E=σ2ϵ0
where ϵ0 is the permittivity of free space.
Step 2: Determine the Total Electric Field
In a parallel plate capacitor, there are two plates, each contributing to the electric field. Therefore, the total electric field (E) between the plates is:
E=σϵ0
Step 3: Relate Surface Charge Density to Charge
The surface charge density σ is related to the charge Q on the plates and the area A of the plates:
σ=QA
Step 4: Substitute for Electric Field
Substituting σ into the expression for the electric field gives:
E=QAϵ0
Step 5: Calculate the Force on One Plate
The force (F) acting on one plate due to the electric field produced by the other plate is given by:
F=Q⋅E
Substituting for E:
F=Q⋅QAϵ0=Q2Aϵ0
Step 6: Include the Effect of Dielectric
If there is a dielectric material between the plates, the permittivity changes. The new permittivity is given by:
ϵ=Kϵ0
where K is the dielectric constant. Thus, the force becomes:
F=Q2Aϵ=Q2AKϵ0
Final Result
The force of attraction between the plates of a parallel plate capacitor with a dielectric is:
F=Q2AKϵ0
The electric field (E) between the plates of a parallel plate capacitor can be derived from the charge on the plates. For a single plate with surface charge density σ, the electric field produced by that plate is given by:
E=σ2ϵ0
where ϵ0 is the permittivity of free space.
In a parallel plate capacitor, there are two plates, each contributing to the electric field. Therefore, the total electric field (E) between the plates is:
E=σϵ0
The surface charge density σ is related to the charge Q on the plates and the area A of the plates:
σ=QA
Substituting σ into the expression for the electric field gives:
E=QAϵ0
The force (F) acting on one plate due to the electric field produced by the other plate is given by:
F=Q⋅E
Substituting for E:
F=Q⋅QAϵ0=Q2Aϵ0
If there is a dielectric material between the plates, the permittivity changes. The new permittivity is given by:
ϵ=Kϵ0
where K is the dielectric constant. Thus, the force becomes:
F=Q2Aϵ=Q2AKϵ0
The force of attraction between the plates of a parallel plate capacitor with a dielectric is:
F=Q2AKϵ0
Topper's Solved these Questions
- ELECTRIC POTENTIAL & CAPACITANCEBook:A2ZChapter:ELECTRIC POTENTIAL & CAPACITANCEExercise:Capacitor With Dielectric
Explore 32 Videos
- ELECTRIC POTENTIAL & CAPACITANCEBook:A2ZChapter:ELECTRIC POTENTIAL & CAPACITANCEExercise:Grouping Of Capacitors
Explore 48 Videos
- ELECTRIC POTENTIAL & CAPACITANCEBook:A2ZChapter:ELECTRIC POTENTIAL & CAPACITANCEExercise:Euipotentials
Explore 45 Videos
- ELECTRIC CHARGE, FIELD & FLUXBook:A2ZChapter:ELECTRIC CHARGE, FIELD & FLUXExercise:Section D - Chapter End Test
Explore 29 Videos
- ELECTROMAGNETIC INDUCTIONBook:A2ZChapter:ELECTROMAGNETIC INDUCTIONExercise:Section D - Chapter End Test
Explore 30 Videos
Similar Questions
separation between the plates of a parallel-plate capacitor is 2 mm and the area of its plates is 5cm2. If the capacitor is charged such that it has 0.01J energy stored in it, the electrostatic force of attraction between its plates is _______N.
View SolutionThe distance between the plates of a parallel plate capacitor is 'd'. The capacitance of the capacitor gets doubled when a metal plate of thicknessd2 is placed between the plates.
View Solution
Knowledge Check
A parallel plate air capacitor has capacity C distance of separation between plates is d and potential difference V is applied between the plates force of attraction between the plates of the parallel plate air capacitor is
AC2V22d2BC2V22dCCV22dDCV2dThe separation between the plates of a charged parallel-plate capacitor is increased. The force between the plates
AincreasesBdecreasesCremains sameDfirst increases then decreasesThe expression for the capacity of a capacitor formed by placing a compound dieletric between the plates of a parallel plate capacitor, as shown in figure , will be (Given area of plate = A)
 Aε0A(d1K1+d2K2+d3K3)Bε0A(d1K1+d2K2+d3K3)Cε0A(K1K2K3)(d1d2d3)Dε0(AK1d1+AK2d2+AK3d3)
Aε0A(d1K1+d2K2+d3K3)Bε0A(d1K1+d2K2+d3K3)Cε0A(K1K2K3)(d1d2d3)Dε0(AK1d1+AK2d2+AK3d3)
The' distance between the plates of a parallel plate capacitor is d. A metal plate of thickness d/2 is placed between the plates. What will e its effect on the capacitance.
View SolutionThe distance between the plates fo a parallel plate capacitor is d. A metal plate of thickness d/2 is placed between the plates, what will be the new capacity ?
View SolutionThe expression for the capacity of the capacitor formed by compound dielectric placed between the plates of a parallel plate capacitor as shown in figure will be
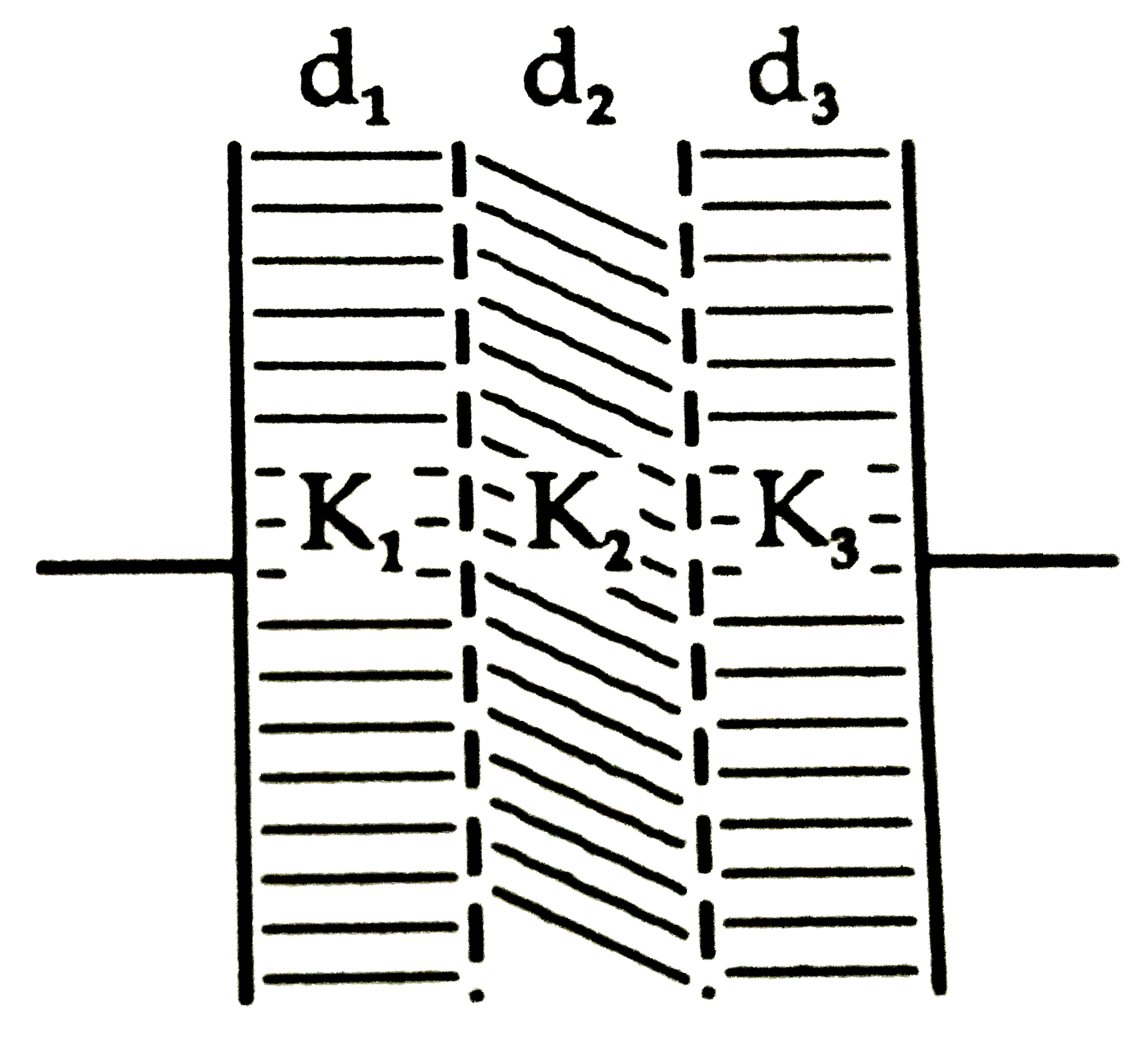
View SolutionThe expression for the capacity of the capacitor formed by compound dielectric placed between the plates of a parallel plate capacitor as shown in figure, will be (area of plate =A)

View SolutionA dielectric slab is placed between the plates of a parallel plate capacitor. Its capacitance
View Solution

