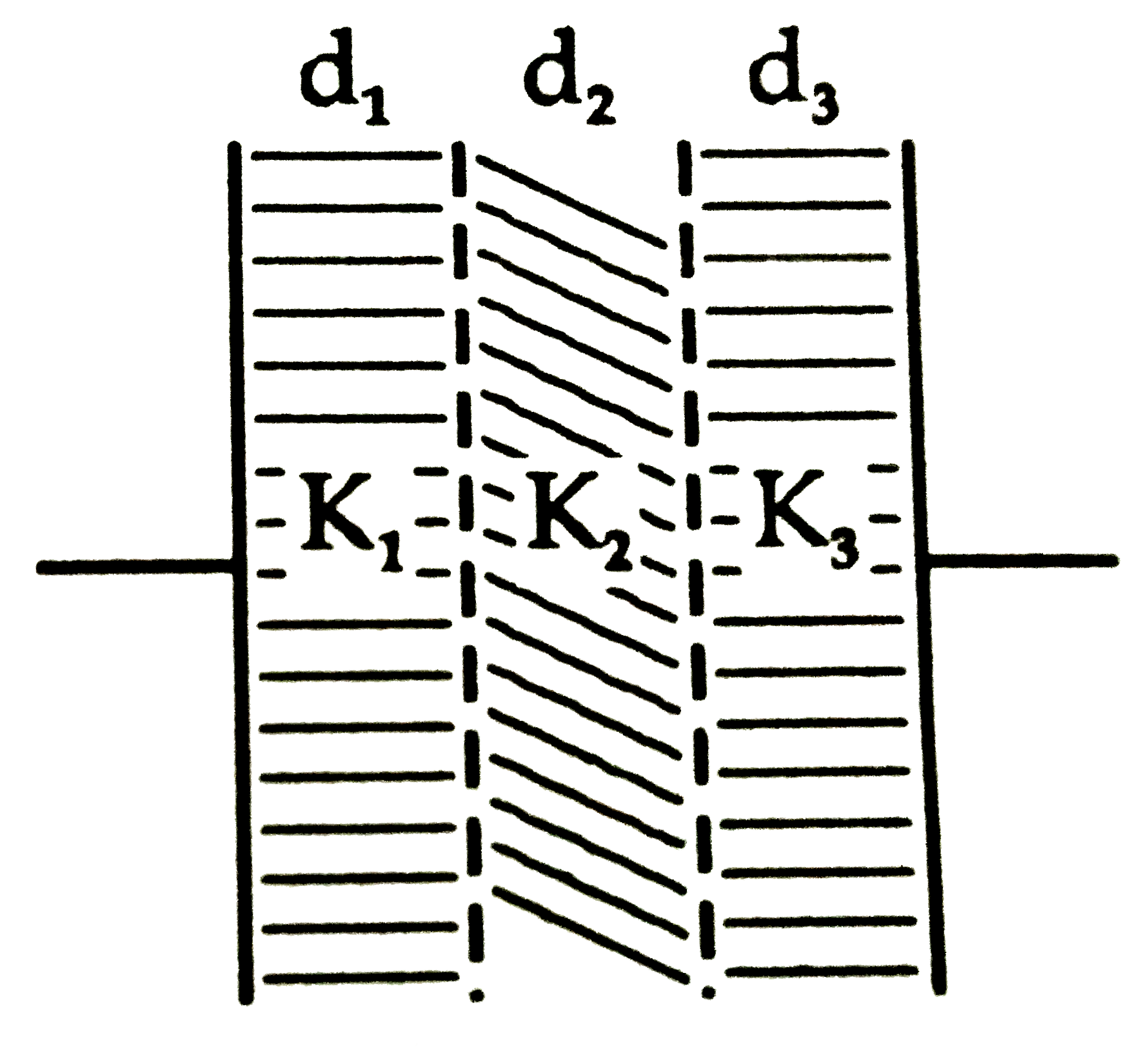
The expression for the capacity of a capacitor formed by placing a compound dieletric between the plates of a parallel plate capacitor, as shown in figure , will be (Given area of plate = A)

A
ε0A(d1K1+d2K2+d3K3)
B
ε0A(d1K1+d2K2+d3K3)
C
ε0A(K1K2K3)(d1d2d3)
D
ε0(AK1d1+AK2d2+AK3d3)
Video Solution
Text Solution
The correct Answer is:a
Capacity of parallel plate condenser =ε0KAd
C=ε0Ad/K. Three capacitances are C1,C2andC3.
∴C1=ε0Ad1/K1,C2=ε0Ad2/K2,C3=ε0Ad3/K3
C1,C2andC3 are in series.
∴1C=1C1+1C2+1C3=d1/K1ε0A+d2/K2ε0A+d3/d3ε0A
⇒1C=1ε0A(d1K1+d2K2+d3K3)
⇒C(d1K1+d2K2+d3K3)=ε0A⇒C=ε0(d1K1+d2K2+d3K3)
|
Topper's Solved these Questions
- ELECTROSTATICSBOOK - MTG-WBJEECHAPTER - ELECTROSTATICSEXERCISE - (WB JEE / WORKOUT )CATEGORY 3 : One or More than One Option Correct Type (2 Marks)
10 Videos
- ELECTROSTATICSBOOK - MTG-WBJEECHAPTER - ELECTROSTATICSEXERCISE - (WB JEE Previous Years Questions ) CATEGORY 1 : Single Option correct Type
23 Videos
- ELECTROSTATICSBOOK - MTG-WBJEECHAPTER - ELECTROSTATICSEXERCISE - (WB JEE Previous Years Questions ) CATEGORY 3 : One or More than One Opion correct Type
4 Videos
- ELECTROMAGNETIC WAVES BOOK - MTG-WBJEECHAPTER - ELECTROMAGNETIC WAVES EXERCISE - WB JEE WORKOUT (CATEGORY 3 : ONE OR MORE THAN ONE OPTION CORRECT TYPE)
10 Videos
- GRAVITATIONBOOK - MTG-WBJEECHAPTER - GRAVITATIONEXERCISE - WB JEE Previous Years Questions (CATEGORY 1: Single Option Correct Type
7 Videos
Similar Questions
Knowledge Check
The expression for the capacity of the capacitor formed by compound dielectric placed between the plates of a parallel plate capacitor as shown in figure, will be (area of plate =A)
 Aε0A(d1K1+d2K2+d3K3)Bε0A(d1+d2+d3K1+K2+K3)Cε0A(K1K2K3)d1d2d3Dε0(AK1d1+AK2d2+AK3d3)
Aε0A(d1K1+d2K2+d3K3)Bε0A(d1+d2+d3K1+K2+K3)Cε0A(K1K2K3)d1d2d3Dε0(AK1d1+AK2d2+AK3d3)Force of attraction between the plates of a parallel plate capacitor is
Aq22ε0AKBq2ε0AKCq2ε0ADq22ε0A2KAs the distance between the plates of a parallel plate capacitor decreased
Achances of electrical break down will increases if potential difference between the plates is kept constant.Bchance of electrical break down will decreases if potential difference between the plates is kept constant.Cchance of electric break down will increases if charge on the plates is kept constantDchance of electrical break down will decrease if charge on the plate is kept constant.
If the plates of a parallel plate capacitor are not equal in area then quantity of charge
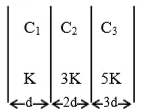
View SolutionIn the reported figure, a capacitor is formed by placing a compound dielectric between the plates of parallel plate capacitor. The expression for the capacity of the said capacitor will be :
(Given area of plate = A)
View SolutionIf we pull apart the plates of parallel plate capacitor then,
View SolutionA dielectric slab is placed between the plates of a parallel plate capacitor. Its capacitance
View SolutionIn a parallel plate capacitor , the capacity increases if
View Solution