If we pull apart the plates of parallel plate capacitor then,
The capacitance increases
Total charge increases
The potential difference increases
Capacitance increases
The correct Answer is:C
To solve the problem regarding the effect of pulling apart the plates of a parallel plate capacitor, we will analyze the situation step by step.
1. Understanding Capacitance: The capacitance C of a parallel plate capacitor is given by the formula:
C=ε0Ad
where ε0 is the permittivity of free space, A is the area of one of the plates, and d is the distance between the plates.
2. Effect of Increasing Distance: When we pull the plates apart, the distance d increases. According to the formula, if d increases, the capacitance C will decrease because capacitance is inversely proportional to the distance between the plates.
3. Considering Charge and Voltage: If the capacitor is connected to a battery, the charge Q on the capacitor is given by:
Q=C⋅V
where V is the voltage across the capacitor. If the capacitance C decreases while the battery is connected, the charge Q will also decrease because V remains constant.
4. Scenario with Disconnected Battery: If the battery is disconnected before we pull the plates apart, the charge Q remains constant. In this case, as the capacitance C decreases (due to increased distance d), the voltage V across the capacitor must increase to maintain the relationship:
Q=C⋅V
Since Q is constant, if C decreases, V must increase.
5. Conclusion: Therefore, if we pull apart the plates of a parallel plate capacitor, the capacitance decreases, and if the capacitor is disconnected from the battery, the voltage across the capacitor increases.
Final Answer:
If we pull apart the plates of a parallel plate capacitor, the capacitance decreases, and if the battery is disconnected, the voltage across the capacitor increases.
C=ε0Ad
where ε0 is the permittivity of free space, A is the area of one of the plates, and d is the distance between the plates.
Q=C⋅V
where V is the voltage across the capacitor. If the capacitance C decreases while the battery is connected, the charge Q will also decrease because V remains constant.
Q=C⋅V
Since Q is constant, if C decreases, V must increase.
If we pull apart the plates of a parallel plate capacitor, the capacitance decreases, and if the battery is disconnected, the voltage across the capacitor increases.
Topper's Solved these Questions
- SAMPLE PAPER 6BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 6EXERCISE - Section-C
6 Videos
- SAMPLE PAPER 6BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 6EXERCISE - Section-C
6 Videos
- SAMPLE PAPER 5BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 5EXERCISE - SECTION - C
6 Videos
- SAMPLE PAPER 7BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 7EXERCISE - SECTION-C
6 Videos
Similar Questions
Column-IColumn-II(A)Plates of an isolated charged parallelPlate air core capacitor are slowly pulled apart(P)Electric energy stored inside capacitor increases in the processincreases in the process(B)A dielectric is slowly inserted inside an isolated and charged parallel plateair cored capacitor to completely fill the space between plates(Q)Force between the two plates of thecapacitor remain unchanged(C)Plates of a parallel plate capacitorconnected across a battery are slowly pulled apart(R) Electric field in the region betweenplates remain unchanged(D)A dielectric slab is slowly inserted inside a parallel plate capacitor conneted acrossa battery to completely fill the space between plates(S)total electric energy stored insidecapacitor decreases in the process(T)Electriec field in the region between plates decreases
View SolutionThere is a parallel plate capacitor of capacitances 2.0μF. The voltage between the plates of parallel plate capacitor is changing at the rate of 6.0Vs−1. What is the displacement current in the capacitor?
View Solution
Knowledge Check
A dielectric slab is placed between the plates of a parallel plate capacitor. Its capacitance
Abecomes zeroBremains the sameCdecreasesDincreasesIn the reported figure, a capacitor is formed by placing a compound dielectric between the plates of parallel plate capacitor. The expression for the capacity of the said capacitor will be :
(Given area of plate = A)
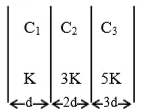 A1534Kε0AdB156Kε0AdC256Kε0A6D96Kε0Ad
A1534Kε0AdB156Kε0AdC256Kε0A6D96Kε0AdIf the plates of a parallel plate capacitor are not equal in area then quantity of charge
Aquantity of charge on the plates will be the same, but nature of charge will differ.Bquantity of charge as well as nature of charge on the plates will be differentCquantity of charge on the plates will be different, but nature of charge will be the same.Dquantity of charge as well as nature of charge will be the same.
How will the electric field between the plates in parallel plate capacitor change, if the charge on the plates is doubled?
View SolutionThe expression for the capacity of the capacitor formed by compound dielectric placed between the plates of a parallel plate capacitor as shown in figure, will be (area of plate =A)

View SolutionIf the plates of a parallel plate capacitor are not equal in area then quantity of charge
View SolutionForce of attraction between the plates of a parallel plate capacitor is
View SolutionAs the distance between the plates of a parallel plate capacitor decreased
View Solution
