The plates of a parallel plate capacitor of capacity 50μC are charged to a potential of 100 volts and then separated from each other so that the distance between then is doubled. How much is the energy spent in doing so
25×10−2J
−12.5×10−2J
−25×10−2J
12.5×10−2J
The correct Answer is:A
To solve the problem, we will follow these steps:
Step 1: Understand the initial conditions
We have a parallel plate capacitor with:
- Initial capacitance C=50μF (microfarads)
- Voltage V=100V (volts)
Step 2: Calculate the initial charge on the capacitor
The charge Q on the capacitor is given by the formula:
Q=C⋅V
Substituting the values:
Q=50×10−6F×100V=5×10−3C
Step 3: Calculate the initial energy stored in the capacitor
The energy U1 stored in a capacitor is given by:
U=12⋅C⋅V2
Substituting the values:
U1=12⋅50×10−6F⋅(100V)2
Calculating:
U1=12⋅50×10−6⋅10000=12⋅50×10−2=25×10−3J=0.025J
Step 4: Determine the new capacitance after doubling the distance
When the distance between the plates is doubled, the new capacitance C2 becomes:
C2=C2=50μF2=25μF
Step 5: Calculate the final energy stored in the capacitor
Since the battery is disconnected, the charge remains the same. The new energy U2 stored in the capacitor is given by:
U2=Q22C2
Substituting the values:
U2=(5×10−3)22⋅25×10−6=25×10−650×10−6=2550=0.5J
Step 6: Calculate the energy spent in separating the plates
The energy spent in doing so is the difference in energy before and after:
Energy spent=U1−U2
Substituting the values:
Energy spent=0.025J−0.5J=−0.475J
Final Answer
The energy spent in separating the plates is 0.025J−0.0125J=0.0125J.
---
We have a parallel plate capacitor with:
- Initial capacitance C=50μF (microfarads)
- Voltage V=100V (volts)
The charge Q on the capacitor is given by the formula:
Q=C⋅V
Substituting the values:
Q=50×10−6F×100V=5×10−3C
The energy U1 stored in a capacitor is given by:
U=12⋅C⋅V2
Substituting the values:
U1=12⋅50×10−6F⋅(100V)2
Calculating:
U1=12⋅50×10−6⋅10000=12⋅50×10−2=25×10−3J=0.025J
When the distance between the plates is doubled, the new capacitance C2 becomes:
C2=C2=50μF2=25μF
Since the battery is disconnected, the charge remains the same. The new energy U2 stored in the capacitor is given by:
U2=Q22C2
Substituting the values:
U2=(5×10−3)22⋅25×10−6=25×10−650×10−6=2550=0.5J
The energy spent in doing so is the difference in energy before and after:
Energy spent=U1−U2
Substituting the values:
Energy spent=0.025J−0.5J=−0.475J
The energy spent in separating the plates is 0.025J−0.0125J=0.0125J.
Topper's Solved these Questions
- ELECTRIC POTENTIAL & CAPACITANCEBOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Capacitor With Dielectric
32 Videos
- ELECTRIC POTENTIAL & CAPACITANCEBOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Grouping Of Capacitors
48 Videos
- ELECTRIC POTENTIAL & CAPACITANCEBOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Euipotentials
45 Videos
- ELECTRIC CHARGE, FIELD & FLUXBOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Section D - Chapter End Test
29 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - A2ZCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Section D - Chapter End Test
30 Videos
Similar Questions
A parallel plate capacitor of capacitance 2 μF is fully charged to a potential difference of 500 volts and then disconnected from the battery. Using insulating handles, separation between the paltes is made thrice the initial value. What will be the new potential difference between the plates of the capacitor and by what amount stored energy changes in this process?
View Solution(a) Find the potential difference between the plates of a parallel plate capacitor of capacitance 5μF if a charge +800μC is placed on one plate and-200μC on another plate.
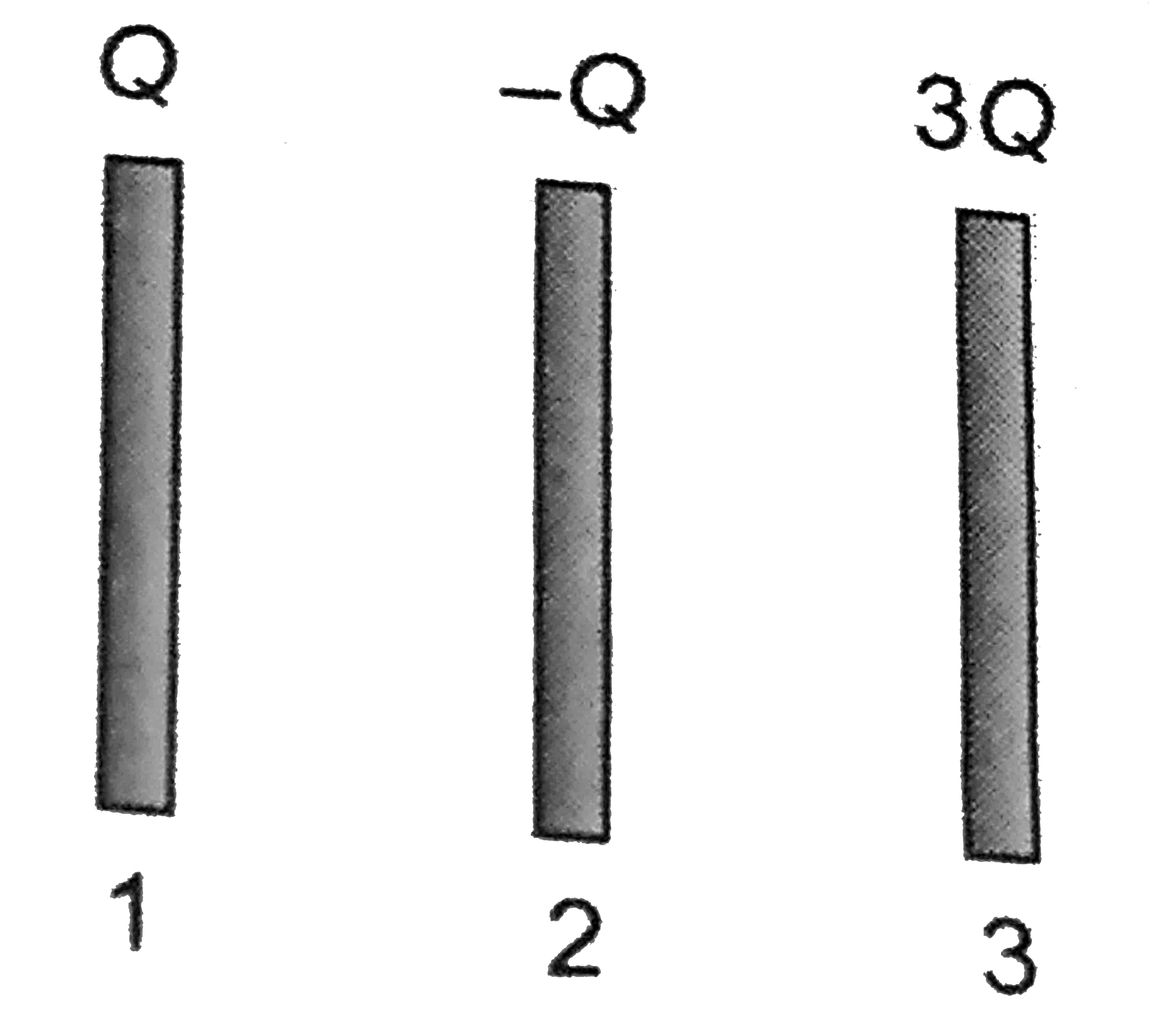
(b) The charege given to plate are as shown. The capacitance between the adjacent plates is C. find the charge on outer surface of plate 3, and potential difference between plate 1 and 2.
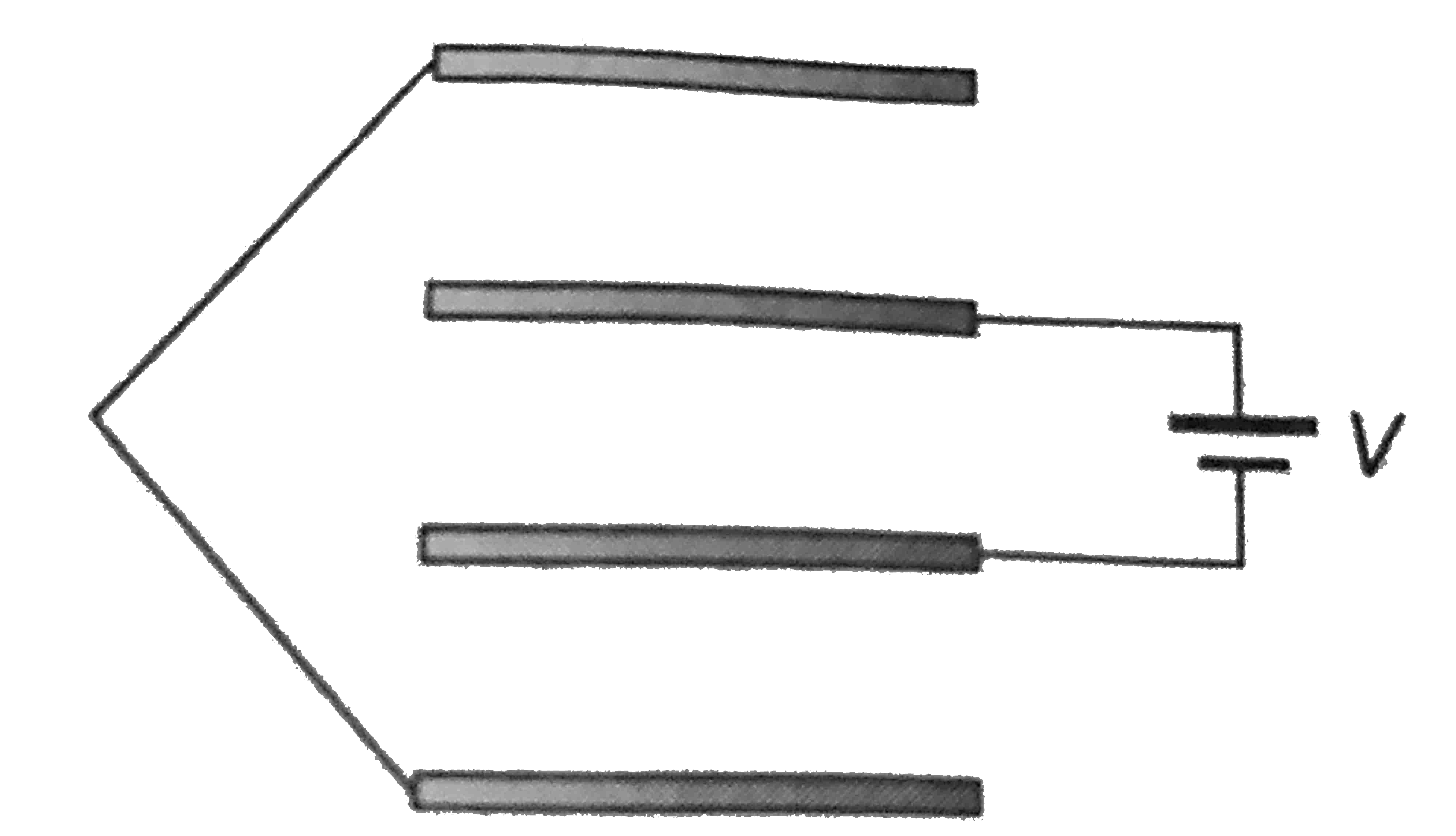
(c) If A is area of each plate and d is separation between adjacent plates, find the charge supplied by battery.
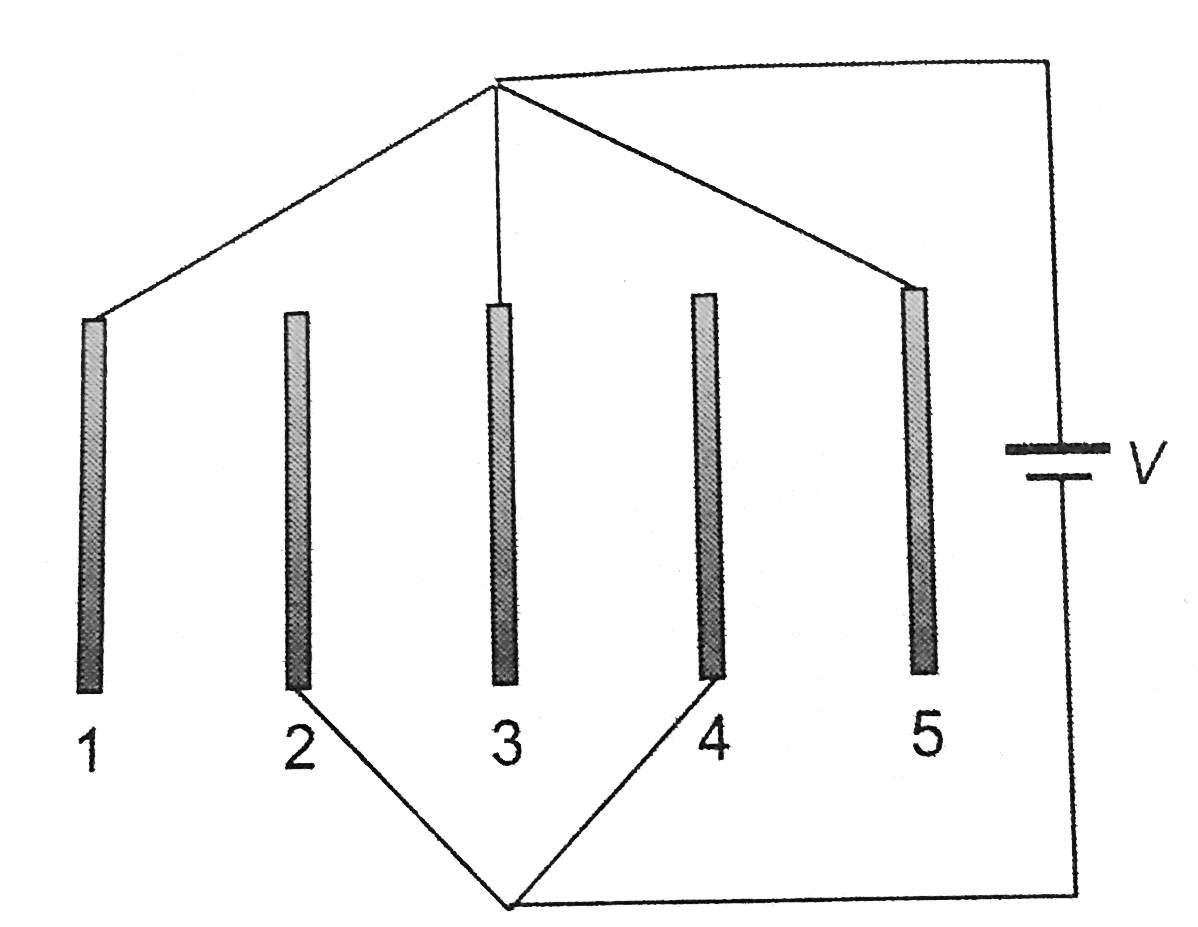
(d) Five idential capacitor plates each of area A are arranged such that adjacent plates are at a distance d apart. the plates are connected to a source of emf V as shown. what is the magnitude and nature of charge on plates 1 and 3 respectively?
View Solution
Knowledge Check
A parallel plate air condenser of capacity 10μF is charged to a potential of 1000V. The energy of the condenser is
A5 JB4 JC2.5 JD10 JA parallel plate capacitor of capacitty 100μF is charged by a battery at 50 volts. The battery remains connected and if the plates of the capacitor are separated so that the distance between them is halved the original distance, the additional energy gives by the battery to the capacitor in Joules is .....
A125×10−3B12.5×10−3C1.25×10−3D0.125×10−3If area of each plate is A and plates are separated from each other by a distance d then Ceq. between A and B is -
 A3∈0AdB∈0A3dC3∈0A2dD2∈0A3d
A3∈0AdB∈0A3dC3∈0A2dD2∈0A3d
The energy of a parallel plate capacitor when connected to a battery is E. With the battery still in connection. If the plates of the capacitor are separated so that the distance between them is twice the original distance then the electrostatic energy becomes
View SolutionA parallel plate capacitor is charged to a potential difference V by a dc source. The capacitor is then disconnected from the source. If the distance between the plates in doubled, state with reason how the following will change,
(i) electric field between the plates,
(ii) capacitance and
(iii) energy stored in the capacitor.
View SolutionA parallel plate capacitor of capacitty 100μF is charged by a battery at 50 volts. The battery remains connected and if the plates of the capacitor are separated so that the distance between them is halved the original distance, the additional energy gives by the battery to the capacitor in Joules is .....
View SolutionThe force between the plates of a parallel plate capacitor of capacitance C and distance of separation of the plates d with a potential difference V between the plates, is.
View SolutionThe force between the plates of a parallel plate capacitor of capacitance C and distance of separation of the plates d with a potential difference V between the plates, is.
View Solution