A charged particle of mass m=2kg and charge 1μC is thrown from a horizontal ground at an angle of 45∘ with horizontal with a spedd of 10m/s. In space a horizontal electric field E=2×107N/C exists. Find the range of the projectile
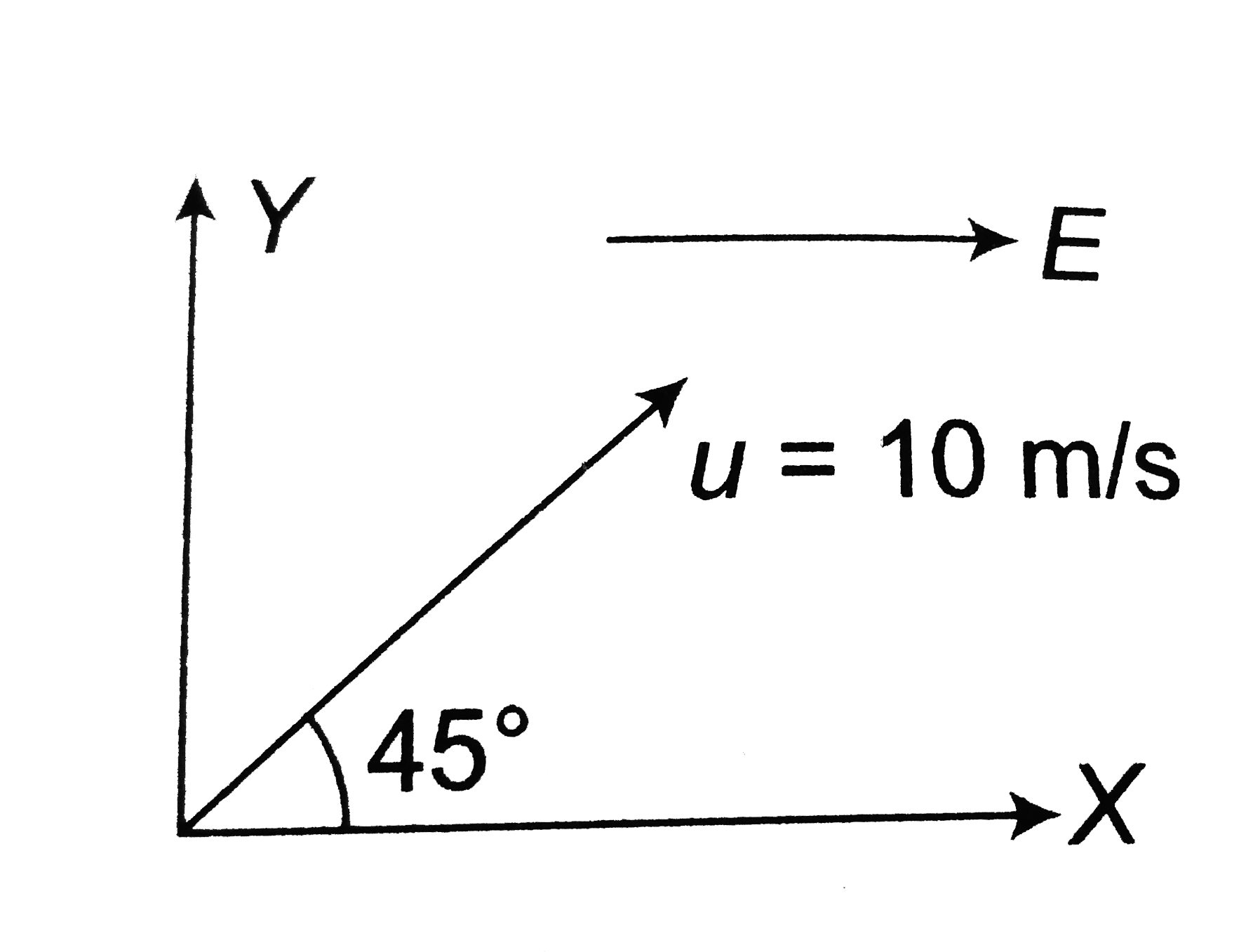
5m
30m
10m
20m
The correct Answer is:D
ax=qEm=10−6×2×1072=10m/s2
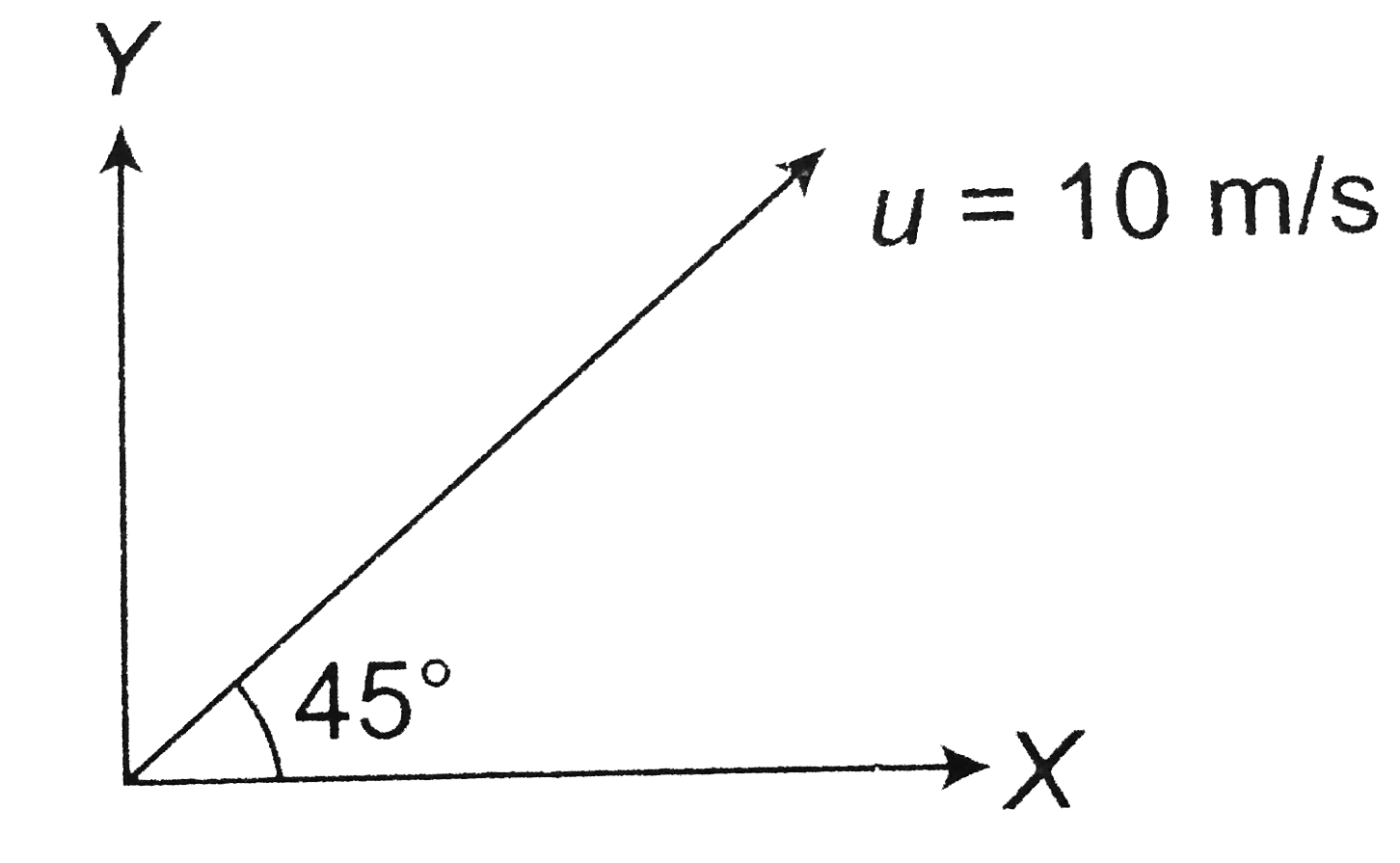
Time of flight T=2usinθg=2×10×1√210=√2s
Hence, Range R=uxT+12axT2
R=10cos45∘×T+12axT2
=10√2×√2+12×10×2=20m
Topper's Solved these Questions
- ELECTRIC CHARGE, FIELD & FLUXBOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Section B - Assertion Reasoning
25 Videos
- ELECTRIC CHARGE, FIELD & FLUXBOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - AIPMTNEET Questions
24 Videos
- ELECTRIC CHARGE, FIELD & FLUXBOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Electric Dipole
29 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - A2ZCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Section D - Chapter End Test
30 Videos
- ELECTRIC POTENTIAL & CAPACITANCEBOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Section D - Chapter End Test
29 Videos
Similar Questions
A charged particle of mass m=1 kg and charge q=2μC is thrown for a horizotal ground at an angle θ=45∘ with speed 20m/s. In space a horizontal electric field E=2×107 V/m exist. Find the range on horizontal ground of the projectile thrown.
View SolutionA charged particle of mass m=1 kg and charge q=2μC is thrown from a horizontal ground at an angle θ=45∘ with the speed 25m/s. In space, a horizontal electric field E=2×107 V/m exists in the direction of motion. Find the range on horizontal ground of the projectile thrown. Take g=10m/s2.
View Solution
Knowledge Check
A charged particle of mass m = 2 kg and charge 1μC is projected from a horizontal ground at an angle θ=45∘ with speed 10ms−1. In space, a horizontal electric field towards the direction of projection E=2×107NC−1 exists. The range of the projectile is
A20 mB60 mC200 mD180 mFrom the ground, a projectile is fired at an angle of 60 degree to the horizontal with a speed of 20 m s−1 The horizontal range of the projectile is
A10√3B20 mC20√3mD40√3
A particle of mass m=0.1kg and having positive charge q=75μC is suspended from a point by a thread of length l=10cm. In the space, a uniform horizontal electric field E=104NC−1 exists. The particle is drawn aside so that the thread becomes vertical and then it is projected horizontally with velocity v such that the particle starts to move along a circle with the same constant speed V. Calculate the radius of the circle and speed v(g=10ms−2).
View SolutionA charged particle of mass 4kg& charge 2C is projected with initial speed 20m/s at an angle 30∘ with the horizontal ( or +x -axis ) .A uniform electric field of intensity 10N/C is present in the region in the +y-direction.Find the maximum height attained by the particle? (Acceleration due to gravity is g=10ms2 in y-direction)
View SolutionA charged particle of mass 4kg& charge 2C is projected with initial speed 20m/s at an angle 30∘ with the horizontal ( or +x -axis ) .A uniform electric field of intensity 10N/C is present in the region in the +y -direction.Find the maximum height attained by the particle? (Acceleration due to gravity is g=10m/s^(2) in y-direction):
View SolutionA charged particle of mass 4kg& charge 2C is projected with initial speed 20m/s at an angle 30^(@) with the horizontal (or+x -axis ) .A uniform electric field of intensity 10N/C is present in the region in the +y-direction.Find the maximum height attained by the particle? (Acceleration due to gravity is g=10m/s^(2) in y- direction):
View SolutionA particle having mass m and charge q is projected at an angle of 75° to the horizontal with a speed u. A uniform electric field E=mgq exists in horizontal direction. Find the time after projection when the velocity of particle makes an angle of 45° with horizontal.
View SolutionA particle of mass m and charge q is thrown with initial velocity v0 at an angle with the horizontal. In space there exist an electric field of strength E at angle β with the downward vertical away from the point of projection. Find the time of flight and range of projectile on horizontal ground
View Solution
