A box of mass 4kg rests upon an inclined plane This inclination is gradually incresed till the box starts sliding down the plane. At this stage slope of the plane is 1 in 3 Find coefficient of friction between the box and the plane What force applied to the box parallel to the plane will just make the box move up the plane ?
The correct Answer is:0.35;26.13N
To solve the problem, we need to find two things: the coefficient of friction (μ) between the box and the inclined plane, and the force required to move the box up the plane.
Step 1: Understanding the Inclined Plane
The slope of the inclined plane is given as 1 in 3. This means that for every 3 units of horizontal distance, the height increases by 1 unit. Therefore, we can define the angle of inclination (θ) using the tangent function:
tan(θ)=oppositeadjacent=13
From this, we can find θ:
θ=tan−1(13)
Step 2: Finding the Coefficient of Friction (μ)
At the point when the box starts sliding down, the angle of repose (α) is equal to θ. The coefficient of friction (μ) can be calculated using:
μ=tan(θ)
We already established that tan(θ)=13. Therefore, the coefficient of friction is:
μ=13
Step 3: Calculating the Forces Acting on the Box
When the box is about to slide down, the forces acting on it are:
- The gravitational force acting down the slope: Fgravity=mgsin(θ)
- The frictional force acting up the slope: Ffriction=μmgcos(θ)
Where:
- m=4kg
- g=10m/s2 (for simplicity)
Step 4: Finding the Normal Force (N)
The normal force (N) acting on the box can be calculated as:
N=mgcos(θ)
Step 5: Force Required to Move the Box Up the Plane
To find the force F required to just move the box up the plane, we need to overcome both the gravitational force pulling it down and the frictional force:
F=mgsin(θ)+μmgcos(θ)
Step 6: Substitute Values
Now substituting the known values:
1. Calculate mgsin(θ):
- sin(θ)=1√10 (from the triangle formed by the slope)
- mgsin(θ)=4×10×13=403
2. Calculate mgcos(θ):
- cos(θ)=3√10
- mgcos(θ)=4×10×3√10=120√10
3. Calculate the frictional force:
- Ffriction=μmgcos(θ)=13×120√10=40√10
Step 7: Total Force Calculation
Now, substituting these into the equation for F:
F=403+40√10
Step 8: Final Calculation
Calculating the total force:
- Convert 40√10 to a decimal or a common denominator to add to 403.
After calculating, we find that the total force required to move the box up the plane is approximately:
F≈26.13N
Summary of Results
1. Coefficient of friction (μ) = 13
2. Force required to move the box up the plane = 26.13N
The slope of the inclined plane is given as 1 in 3. This means that for every 3 units of horizontal distance, the height increases by 1 unit. Therefore, we can define the angle of inclination (θ) using the tangent function:
tan(θ)=oppositeadjacent=13
From this, we can find θ:
θ=tan−1(13)
At the point when the box starts sliding down, the angle of repose (α) is equal to θ. The coefficient of friction (μ) can be calculated using:
μ=tan(θ)
We already established that tan(θ)=13. Therefore, the coefficient of friction is:
μ=13
When the box is about to slide down, the forces acting on it are:
- The gravitational force acting down the slope: Fgravity=mgsin(θ)
- The frictional force acting up the slope: Ffriction=μmgcos(θ)
- m=4kg
- g=10m/s2 (for simplicity)
The normal force (N) acting on the box can be calculated as:
N=mgcos(θ)
To find the force F required to just move the box up the plane, we need to overcome both the gravitational force pulling it down and the frictional force:
F=mgsin(θ)+μmgcos(θ)
Now substituting the known values:
1. Calculate mgsin(θ):
- sin(θ)=1√10 (from the triangle formed by the slope)
- mgsin(θ)=4×10×13=403
- cos(θ)=3√10
- mgcos(θ)=4×10×3√10=120√10
- Ffriction=μmgcos(θ)=13×120√10=40√10
Now, substituting these into the equation for F:
F=403+40√10
Calculating the total force:
- Convert 40√10 to a decimal or a common denominator to add to 403.
F≈26.13N
1. Coefficient of friction (μ) = 13
2. Force required to move the box up the plane = 26.13N
Topper's Solved these Questions
- LAWS OF MOTIONBook:PRADEEPChapter:LAWS OF MOTIONExercise:JEE (Main and Advanced)/ Medical Entrance Special
Explore 93 Videos
- LAWS OF MOTIONBook:PRADEEPChapter:LAWS OF MOTIONExercise:Integer Type Questions
Explore 7 Videos
- LAWS OF MOTIONBook:PRADEEPChapter:LAWS OF MOTIONExercise:Fill in the blanks
Explore 20 Videos
- KINEMATICSBook:PRADEEPChapter:KINEMATICSExercise:1 NCERT Comprehension
Explore 4 Videos
- MATHEMATICAL TOOLSBook:PRADEEPChapter:MATHEMATICAL TOOLSExercise:Fill in the blanks
Explore 5 Videos
Similar Questions
A mass of 4 kg rest on a horizontal plane . The plane is gradually inclined until an angle 0=15∘ with the horizontal and the mass just begins to slide . What is the coefficient of static friction between the block and the surface ?
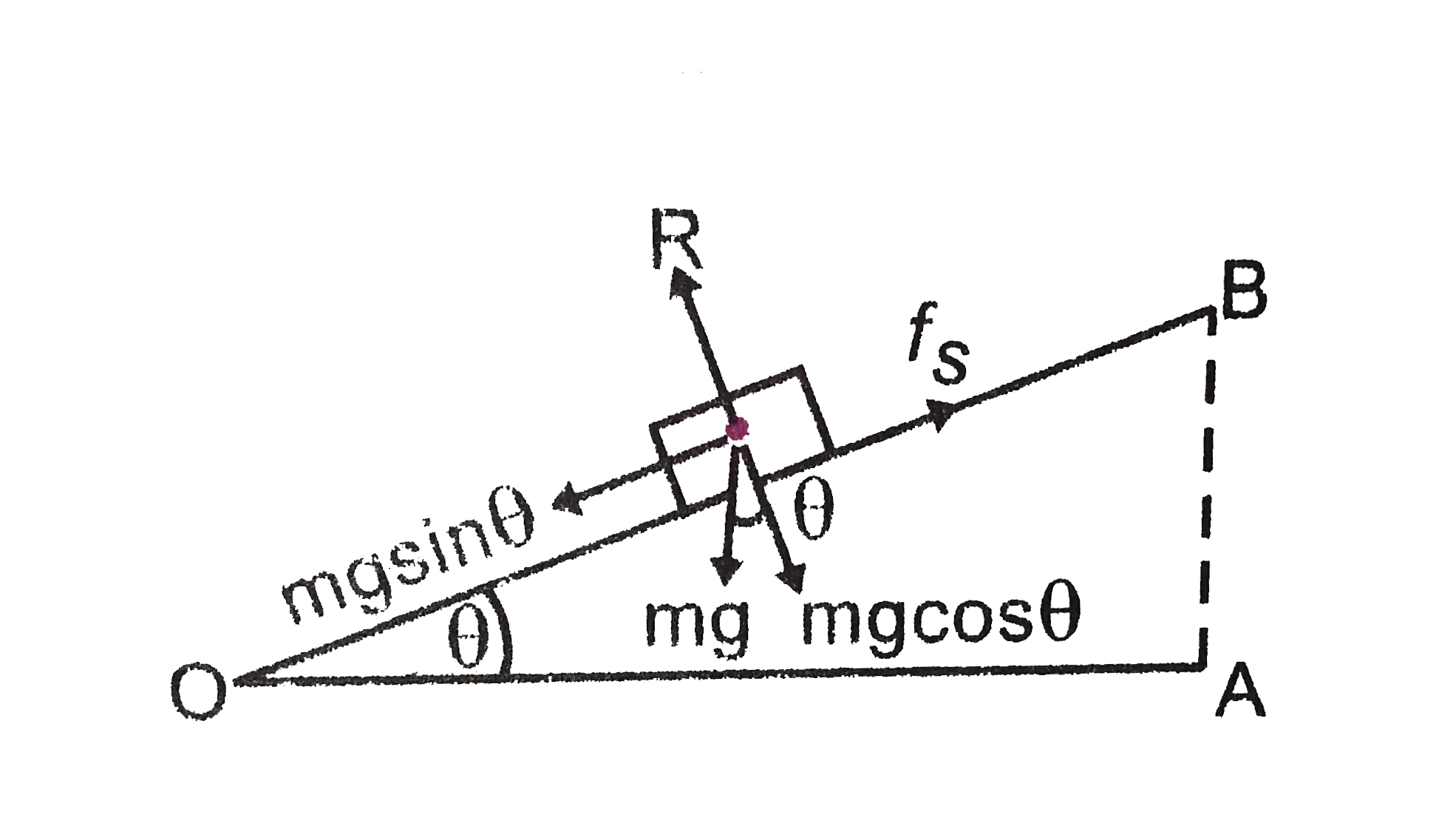
View SolutionA block of mas M is resting on an inclined plane as shown in the figure. The inclination of the plane to the horizontal is gradually increased. It is found that when the angle of inclination is θ the block just begins to slide down the plane. What is the minimum force F applied parallel to the plane that would just make the block move up the plane ?
View Solution
Knowledge Check
A block of mass 5 kg is placed on a rough inclined plane. The inclination of the plane is gradually increased till the block just begins to slide down. The inclination of the plane is than 3 in 5. The coefficient of friction between the block and the plane is (Take, g=10m/s2)
A35B34C45D23A block of mass 4kg rests on an an inclined plane. The inclination of the plane is gradually increased. It is found that when the inclination is 3 in 5 (sinθ=35) the block just begins to slide down the plane. The coefficient of friction between the block and the plane is.
A0.4B0.6C0.8D0.75A block of mass m is resting on an inclined plane. The inclination of the plane to the horizontal is gradually increased. It is found that when angle of inclination is θ, the block just begins to slide down the plane. What is the minimum force F applied parallel to the plane that would just make the block move up the plane?
A2mgsinθBmgsinθCmgcosθD2mgcosθ
A block of mass 4kg rests on a rough horizontal plane. The plane is gradually inclined until at an angle θ=60∘ , with the vertical, the mass just begins to side. What is the coefficient of static friction between the block and the plane?
View SolutionA block of mass m slides down an inclined plane which makes an angle θ with the horizontal. The coefficient of friction between the block and the plane is μ. The force exerted by the block on the plane is
View SolutionA block is placed on an inclined plane. The angle of inclination of the plane is such that the block slides down the plane at a constant speed. The coefficient of kinetic friction is
View SolutionA block of mass m slides down an inclined plane of inclination θ with uniform speed. The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is
View SolutionA block of mass m slides down an inclined plane of inclination θ with uniform speed The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is .
View Solution

