A block of mass 4kg rests on a rough horizontal plane. The plane is gradually inclined until at an angle θ=60∘ , with the vertical, the mass just begins to side. What is the coefficient of static friction between the block and the plane?
√3
12
1√2
1√3
The correct Answer is:D
To solve the problem, we need to determine the coefficient of static friction (μ) between the block and the inclined plane when the block just begins to slide at an angle of θ = 60° with the vertical.
1. Identify the Forces Acting on the Block:
- The weight of the block (W) acts downwards, which can be calculated as:
W=mg=4kg×g
- The gravitational force can be resolved into two components:
- Perpendicular to the inclined plane: W⊥=mgcos(30∘)
- Parallel to the inclined plane: W∥=mgsin(30∘)
2. Calculate the Components of the Weight:
- Using g≈9.81m/s2:
W⊥=4gcos(30∘)=4g(√32)=2√3g
W∥=4gsin(30∘)=4g(12)=2g
3. Determine the Normal Force (N):
- The normal force (N) is equal to the perpendicular component of the weight:
N=W⊥=2√3g
4. Determine the Maximum Static Friction (F_max):
- The maximum static friction force (F_max) can be expressed as:
Fmax=μN=μ(2√3g)
5. Set Up the Equation for Forces:
- At the point of impending motion, the maximum static friction equals the parallel component of the weight:
Fmax=W∥=2g
- Therefore, we can equate the two expressions:
μ(2√3g)=2g
6. Solve for the Coefficient of Static Friction (μ):
- Cancel g from both sides (assuming g≠0):
μ(2√3)=2
- Rearranging gives:
μ=22√3=1√3
Final Answer:
The coefficient of static friction (μ) between the block and the plane is:
μ=1√3
- The weight of the block (W) acts downwards, which can be calculated as:
W=mg=4kg×g
- The gravitational force can be resolved into two components:
- Perpendicular to the inclined plane: W⊥=mgcos(30∘)
- Parallel to the inclined plane: W∥=mgsin(30∘)
- Using g≈9.81m/s2:
W⊥=4gcos(30∘)=4g(√32)=2√3g
W∥=4gsin(30∘)=4g(12)=2g
- The normal force (N) is equal to the perpendicular component of the weight:
N=W⊥=2√3g
- The maximum static friction force (F_max) can be expressed as:
Fmax=μN=μ(2√3g)
- At the point of impending motion, the maximum static friction equals the parallel component of the weight:
Fmax=W∥=2g
- Therefore, we can equate the two expressions:
μ(2√3g)=2g
- Cancel g from both sides (assuming g≠0):
μ(2√3)=2
- Rearranging gives:
μ=22√3=1√3
The coefficient of static friction (μ) between the block and the plane is:
μ=1√3
Similar Questions
A mass of 4 kg rest on a horizontal plane . The plane is gradually inclined until an angle 0=15∘ with the horizontal and the mass just begins to slide . What is the coefficient of static friction between the block and the surface ?
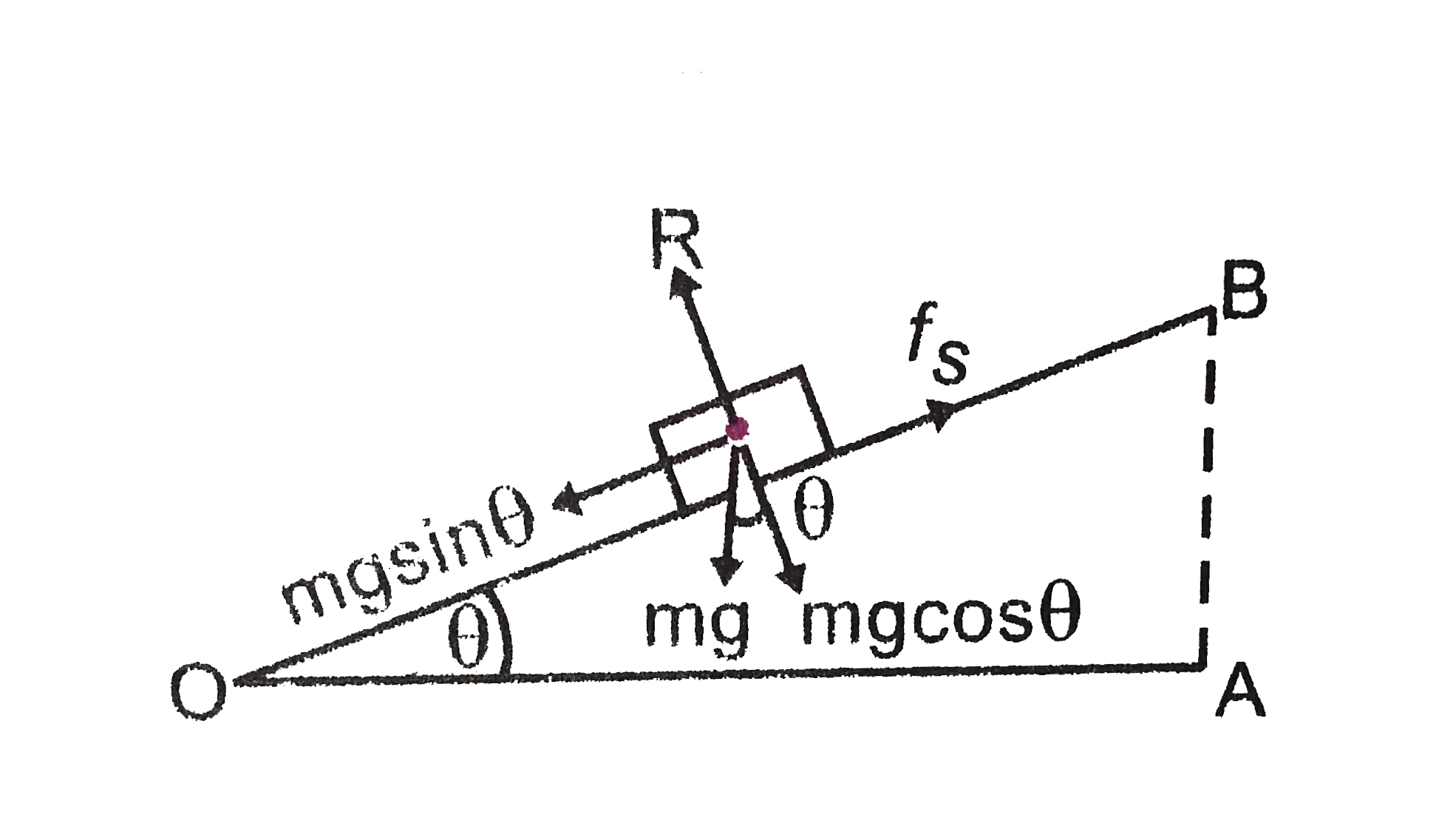
View SolutionA mass of 4 kg rests on a horizontal plane. When the plane is gradually inclined to an angle 0 -15° with the horizontal, the mass just begins to slide. What is the coefficient of static friction between the block and the surface? [Given, tan 15° = 0.2679)
View Solution
Knowledge Check
A block is stationary on an inclined plane If the coefficient of friction between the block and the plane is μ then
 .Aμ>tanθBf=mgsinθCf=μmgcosθDthe reaction of the ground on the block is mg cos θ
.Aμ>tanθBf=mgsinθCf=μmgcosθDthe reaction of the ground on the block is mg cos θA block of mass m lying on a rough horizontal plane is acted upon by a horizontal force P and another force Q inclined at an angle θ to the vertical. The minimum value of coefficient of friction of friction between the block and the surface for which the block will remain in equilibrium is
 AP+Qsinθmg+QcosθBPcosθ+Omg−QsinθCP+Qcosθmg+QsinθDΨnθ−Qmg−Qcosθ
AP+Qsinθmg+QcosθBPcosθ+Omg−QsinθCP+Qcosθmg+QsinθDΨnθ−Qmg−QcosθA block of mass 5 kg is placed on a rough inclined plane. The inclination of the plane is gradually increased till the block just begins to slide down. The inclination of the plane is than 3 in 5. The coefficient of friction between the block and the plane is (Take, g=10m/s2)
A35B34C45D23
The coefficient of friction between the block and the inclined plane is μ.
View SolutionA block of mass 5 kg rests on a inclined plane at an angle of 30∘ with the horizontal. If the block just begins to slide, then what is the coefficient of static friction between the block and the surface?
View SolutionA block of mass 5 kg rests on a inclined plane at an angle of 30∘ with the horizontal. If the block just begins to slide, then what is the coefficient of static friction between the block and the surface?
View SolutionA box of mass 4kg rests upon an inclined plane This inclination is gradually incresed till the box starts sliding down the plane. At this stage slope of the plane is 1 in 3 Find coefficient of friction between the box and the plane What force applied to the box parallel to the plane will just make the box move up the plane ?
View SolutionA block of mass m lying on a rough horizontal plance is acted upon by a horizontal force P and another force Q inclined at an angle θ to the vertical. The block will remain in equilibrium, if the coefficient of friction between it and the surface is
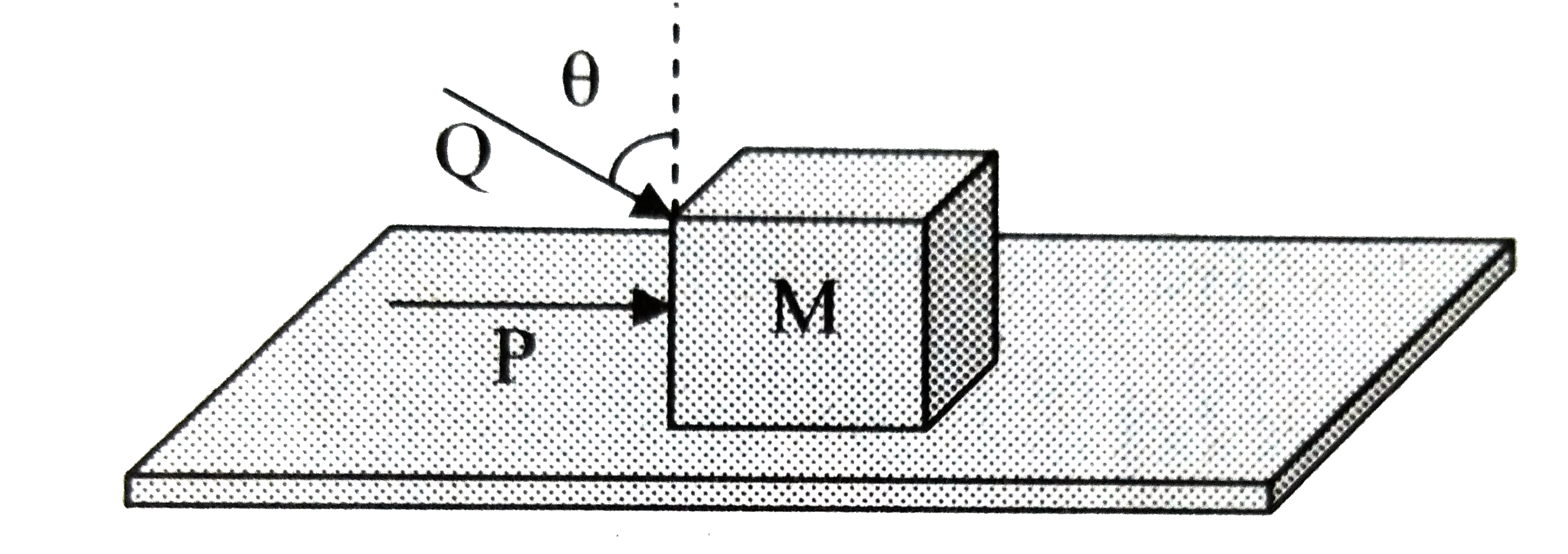
View Solution
