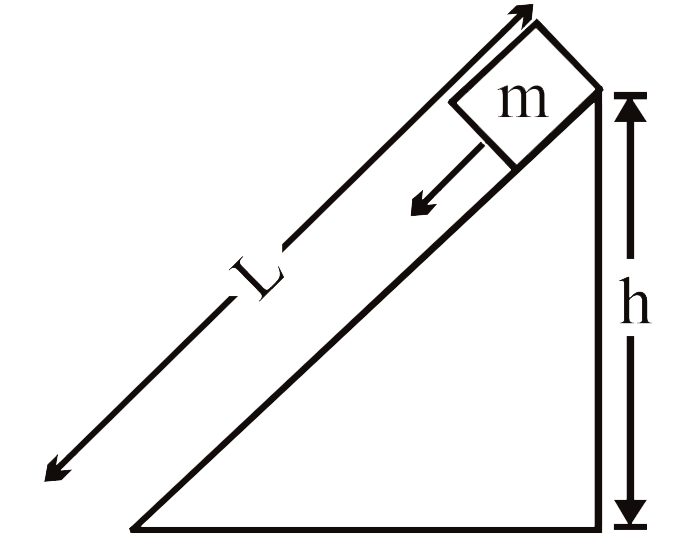
A body of mass m is released from the top of a rough inclined plane of length l and height h If f is the force of friction prove that the body will reach the bottom with a velocity $υ = \sqrt{\frac{2}{m} (m g h - f l)}$ .

Video Solution

Text Solution

Verified by Experts

On reaching the battom loss in $P . E$ = mgh
Gain in $K . E = \frac{1}{2} m υ^{2}$ and
work done against friction $f \times l$
According to the law of conservation of energy
$\frac{1}{2} m υ^{2} + f \times l = m g h$
$υ = \sqrt{\frac{2}{m} (m g h - f \times l)}$
which was to be proved.

|

Updated on:21/07/2023

Class 11 PHYSICS NEWTONS LAW OF MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A block of mass $m$ is released from the top of a mooth inclined plane of height $h$ its speed at the bottom of the plane is proportion to
A $m^{0}$
B $m$
C $m^{2}$
D $m^{- 1}$
Question 2 - Select One
An object of mass m is released from rest from the top of a smooth inclined plane of height h. Its speed at the bottom of the plane is proportional to
A $m^{0}$
B $m$
C $m^{2}$
D $m^{- 1}$
Question 3 - Select One
A body of mass m slides down a rough plane of inclination $α$ . If $μ$ is the coefficient of friction, then acceleration of the body will be
A $g sin α$
B $μ cos α$
C $g (sin α - μ cos α)$
D $g (cos α - μ sin α)$

PRADEEP-LAWS OF MOTION-Problems for practice

Home
Ask Doubt
Profile