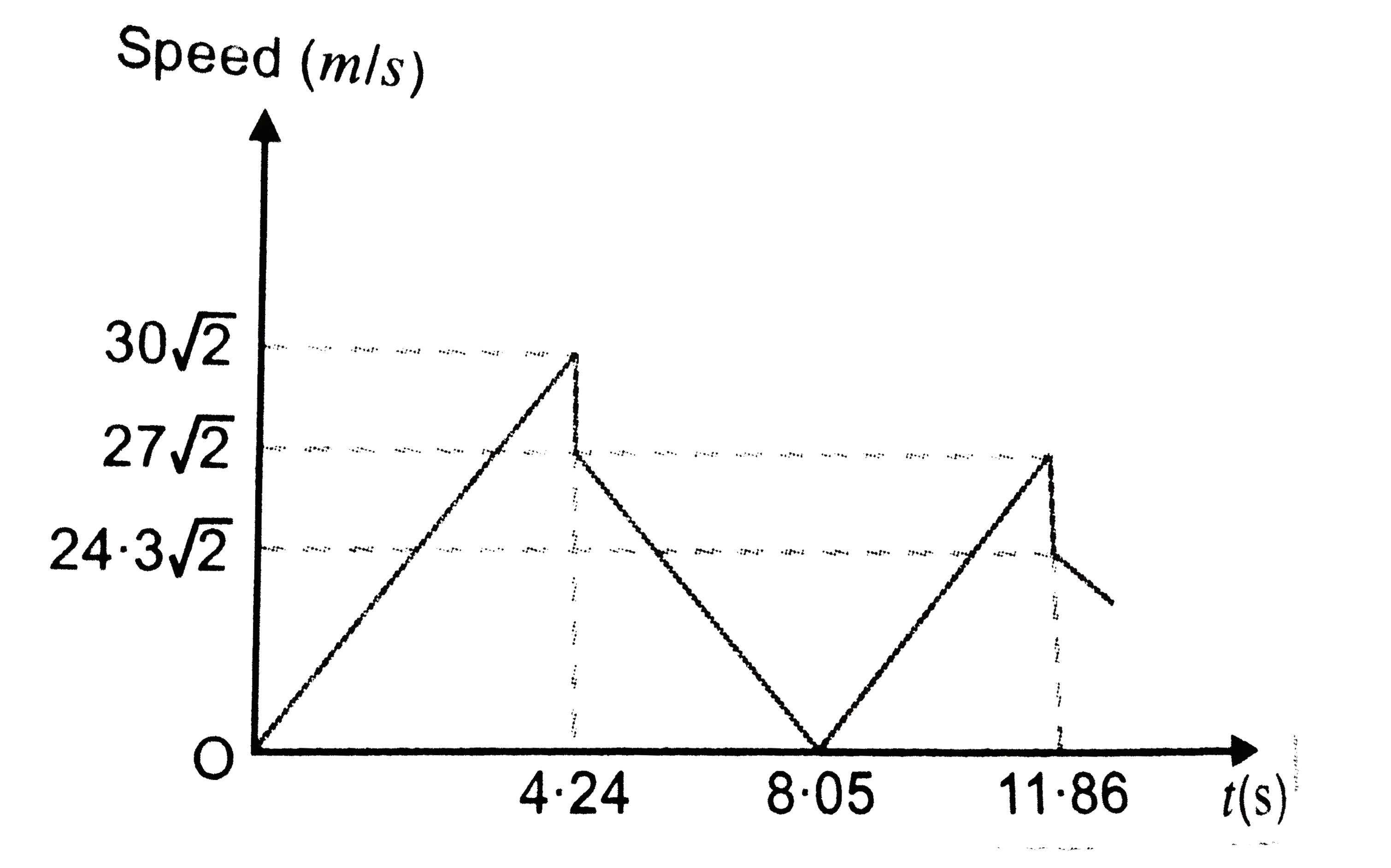
A ball is dropped from a height of a height of 90 m on a floor. At each collsion with the floor , the ball loses one - tenth of its speed . Plot the speed -time graph of its motion between t 0 to 12 s.
Taiking vertical downward motion of ball from a height 90m, we have
u=0,a=10m/s2,S=90m,t=?,v=?
t=√2Sa=√2×90910)=3sqr2s=4.24s
v=√2aS=√2×10×x90=30√2m/s
Rebound velocity of ball, u'=910v=910×30√2=27√2m/s
Time to reach the hight the highest point is , t'=u'a=(27√2010=2.7√2=3.81s
Total time =t+t'=4.24+3.81=8.05s
The ball will take further 3.81s to fall back to floor, wher its velocity b efore striking the floor
=27√2m/s.
Veloity of ball after striking the floor
=910×27√2=24.3√3m/s
Total time elapsed before upward motion of ball
=8.05+3.81=11.86s
Thus the speed-time graph of this of motion will be as shown in Fig. 2 (NCT).3.
 .
.
Topper's Solved these Questions
- KINEMATICSBook:PRADEEPChapter:KINEMATICSExercise:Additional Exercises
Explore 13 Videos
- KINEMATICSBook:PRADEEPChapter:KINEMATICSExercise:Motion
Explore 25 Videos
- KINEMATICSBook:PRADEEPChapter:KINEMATICSExercise:Advanced Problems
Explore 20 Videos
- GRAVIATIONBook:PRADEEPChapter:GRAVIATIONExercise:Assertion-Reason Type Questions
Explore 19 Videos
- LAWS OF MOTIONBook:PRADEEPChapter:LAWS OF MOTIONExercise:Assertion- Reason Type Questions
Explore 17 Videos
Similar Questions
A ball is dropped from a height of 80 m on a floor. At each collision, the ball loses half of its speed. Plot the speed-time graph and velocity-time graph of its motion till two collisions With the floor. [Take g=10m/s2]
View SolutionA ball is dropped from a height h on to a floor . If the cofficient of restitution is e, calculate the height the ball first rebounds ?
View Solution
Knowledge Check
A ball is dropped from a height of 20m on a floor for which e=1/2. The height attained by the ball after the second collision
A1.25mB2.5mC5mD10mA ball is dropped from a certain height on a horizontal floor. The coefficient of restitution between the ball and the floor is 12. The displacement time graph of the ball will be.
A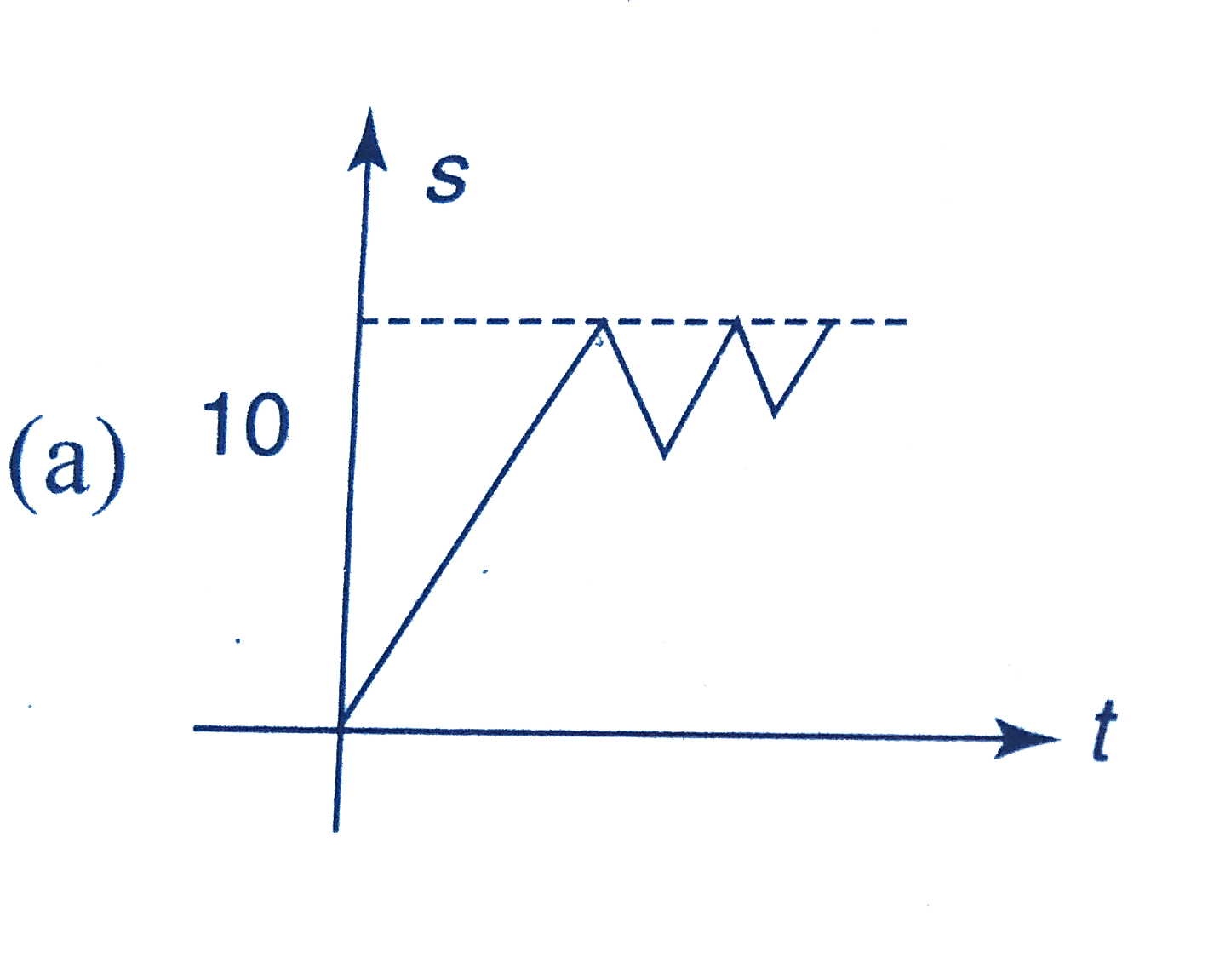 .B
.B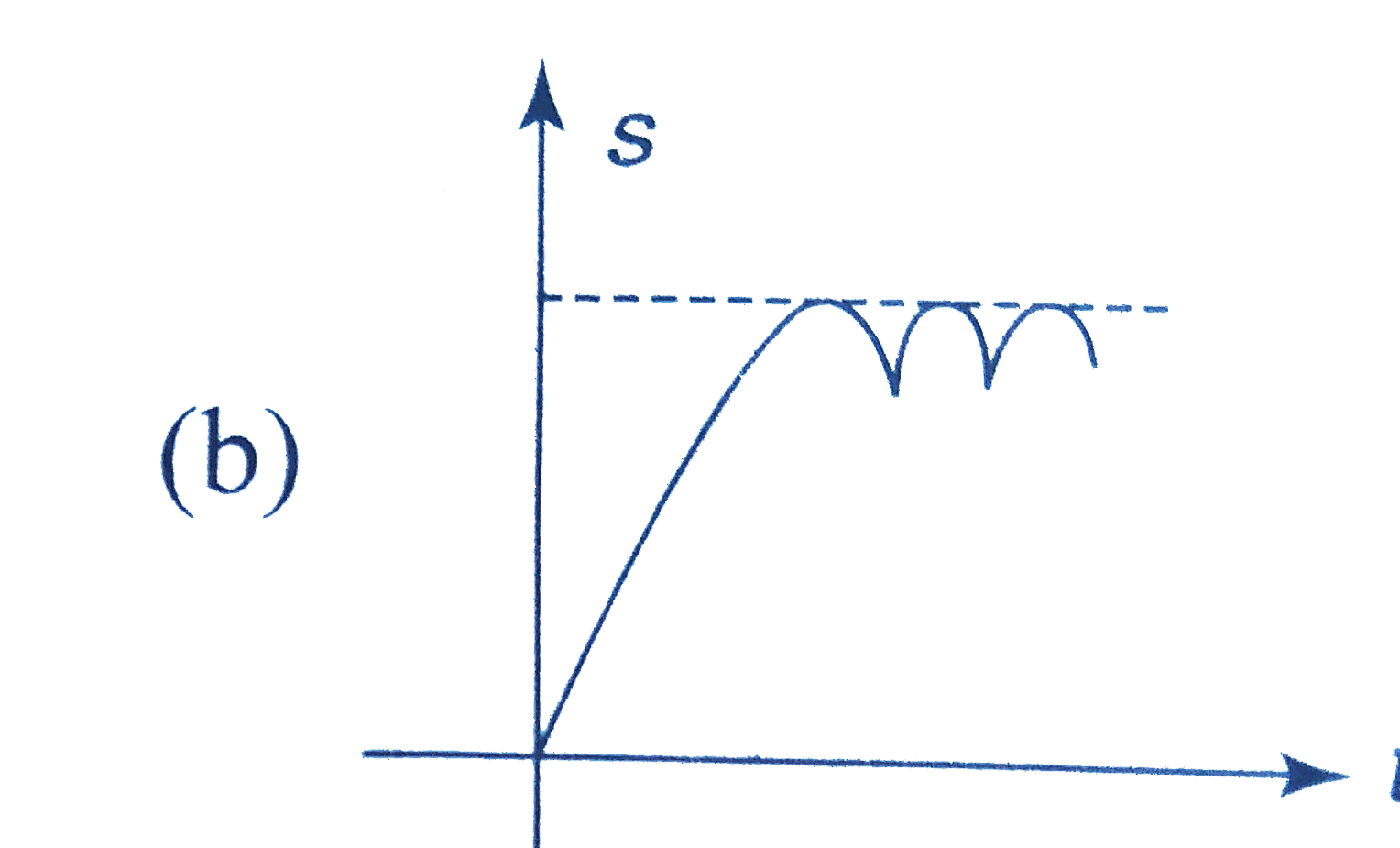 .C
.C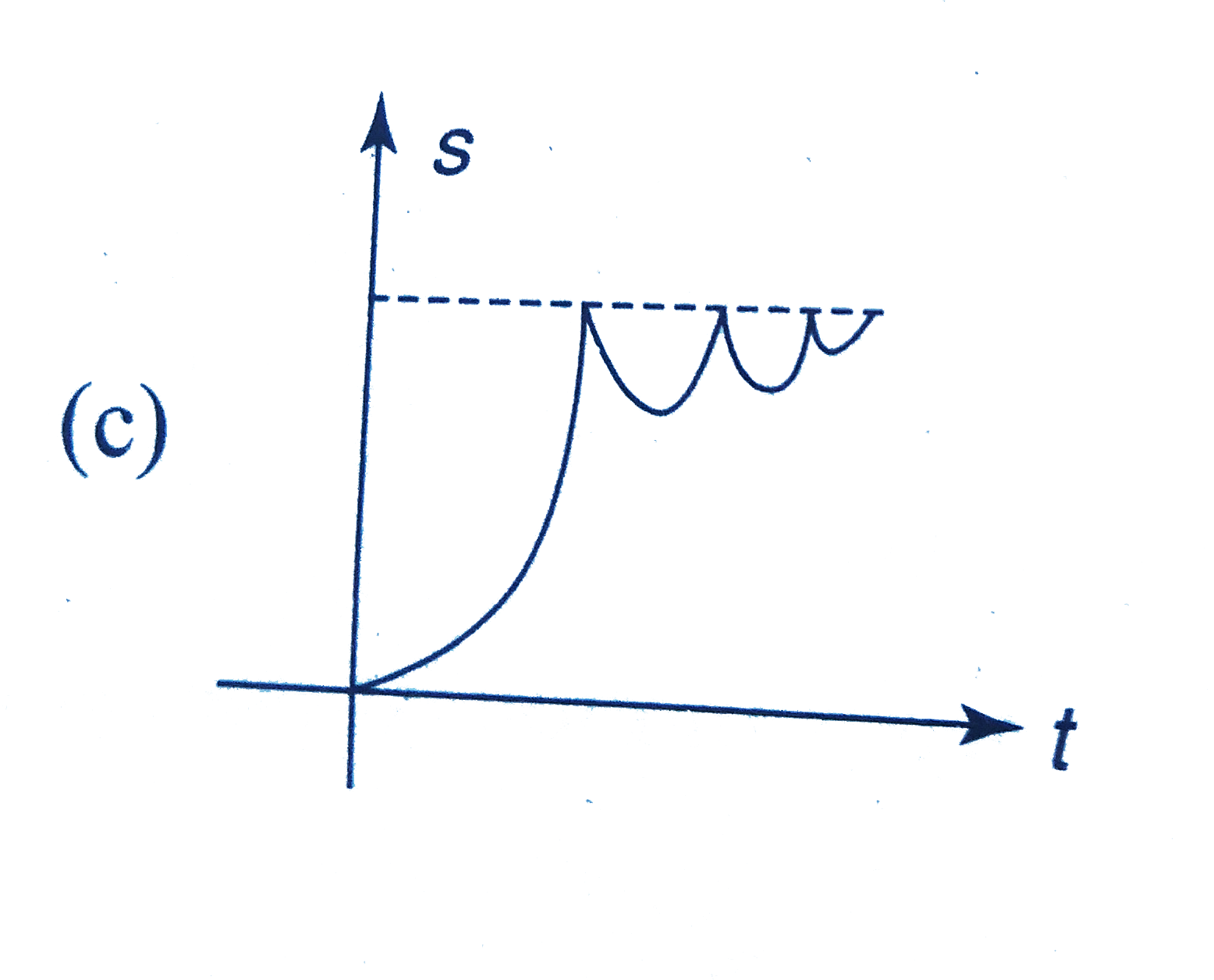 .D
.D .
.A ball is dropped from certain height on a glass floor so that it rebounds elastically to the same height. If the process continues, the velocity -time graph for such a motion would be -
 AIBiiCiiiDiv
AIBiiCiiiDiv
A ball is dropped from a height h on to a floor. If in each collision its speed becomes e times of its striking value (a) find the time taken by ball to stop rebounding (b) find the total change in momentum in this time (c) find the average force exerted by the ball on the floor using results of part (a) and (b).
View SolutionIf a ball is dropped from height 2 metre on a smooth eleastic floor, then the time period of oscillation is
View SolutionAn inelastic ball is dropped from a height 100 meter. If due to impact it loses 35% of its energy the ball will rise to a height of
View SolutionA ball is dropped from a height h. As it bounces off the floor, its speed is 80 percent of what it was just before it hit the floor. The ball will then rise to a height of most nearly
View SolutionA ball is dropped from a height h on a floor. The coefficient of restitution for the collision between the ball and the floor is e. The total distance covered by the ball before it comes to the rest.
View Solution

