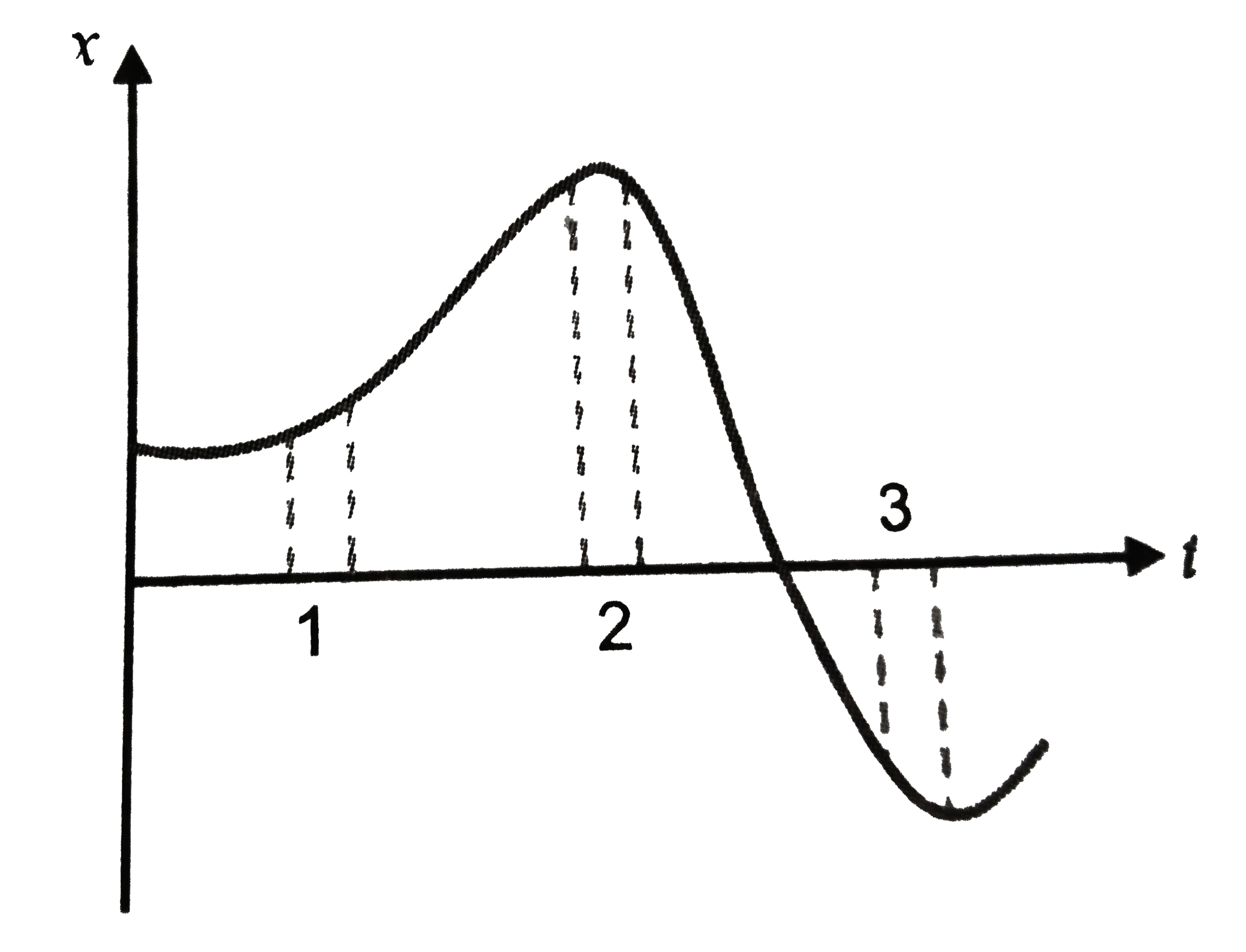
Fig. 2 (NCT).9 show the x−t plot of a particle in one dimensional motion. Three different equal intervals of time are shown. In which interval the average speed is greatest and in which it is the least ? Give the sign of average speed for each interval.
.
We kinow that aveage speed in a sma,, interval of time is eqqual to the slope of x−t graph in that ineraval of time. The average speed is the greatest in the interval 3 because slope is greatest and the average speed is leaset in inerval 2 necause slope is least there.
The average speed is positive in intervals 1 and 2 because slope of x−t is positive there and average speed is negative in interval 3 becauses the slpe of x−t is negative.
Topper's Solved these Questions
- KINEMATICSBOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - Additional Exercises
13 Videos
- KINEMATICSBOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - Motion
25 Videos
- KINEMATICSBOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - Advanced Problems
20 Videos
- GRAVIATIONBOOK - PRADEEPCHAPTER - GRAVIATIONEXERCISE - Assertion-Reason Type Questions
19 Videos
- LAWS OF MOTIONBOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Assertion- Reason Type Questions
17 Videos
Similar Questions
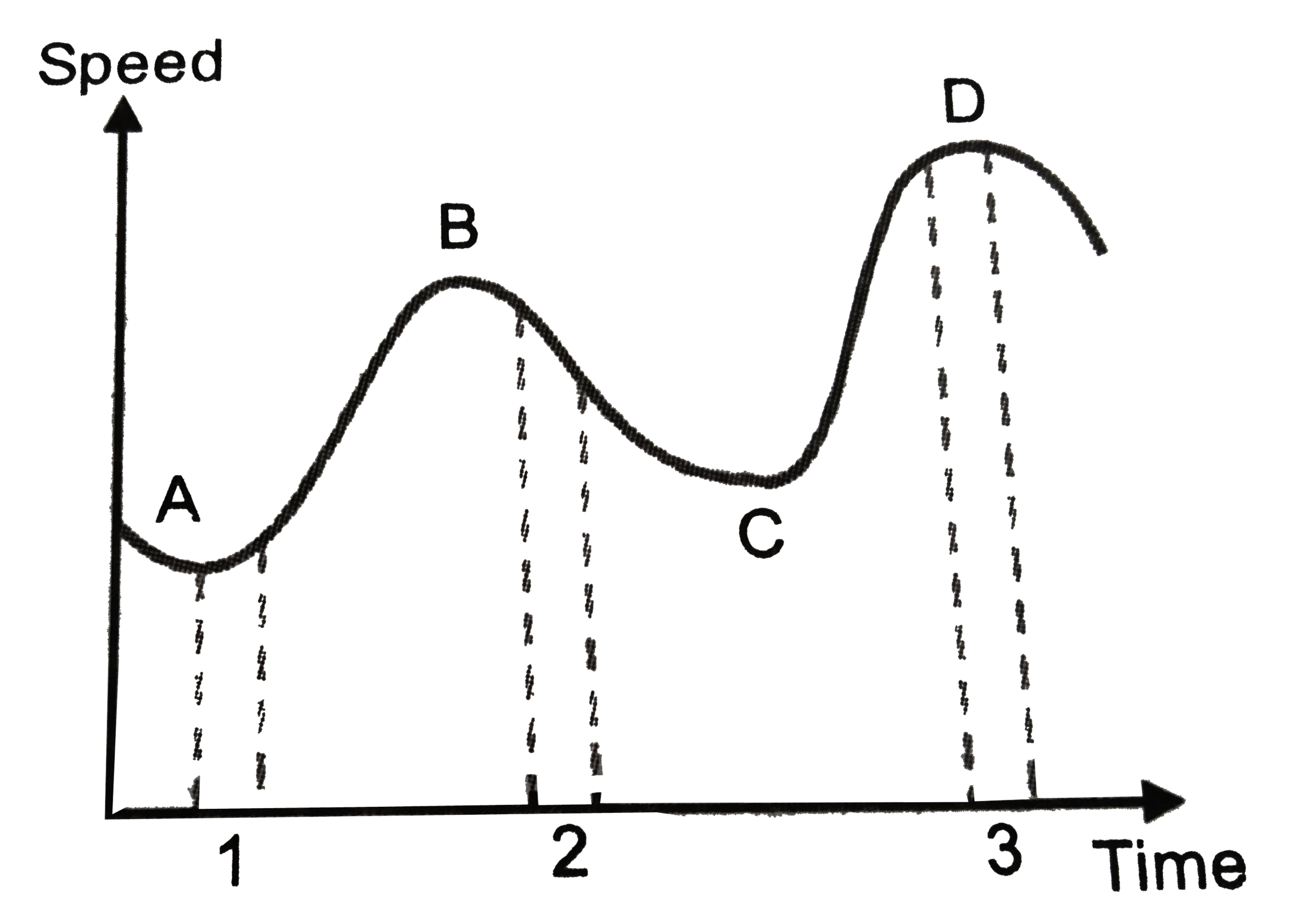
Fig. 2 (NCT). 10 . Give a speed-tiem graph of a particle in one dimenstional motion. Three different equal intervals of time are shwon. In which interval is the average acceleration graeatest in magnitude ? In which interval is the average speed greatest ? Choosing the positive direction as the constant direction of motion, give the signs of u and a in the three intervals. What are the acclerations at teh points A,B,C and D ?
.
View SolutionFind average speed in time interval t= 2 to t=10s
View Solution
Knowledge Check
The velocity-time plot is shown in figure. Find the average speed in time interval t=0 to t=40s during the period.
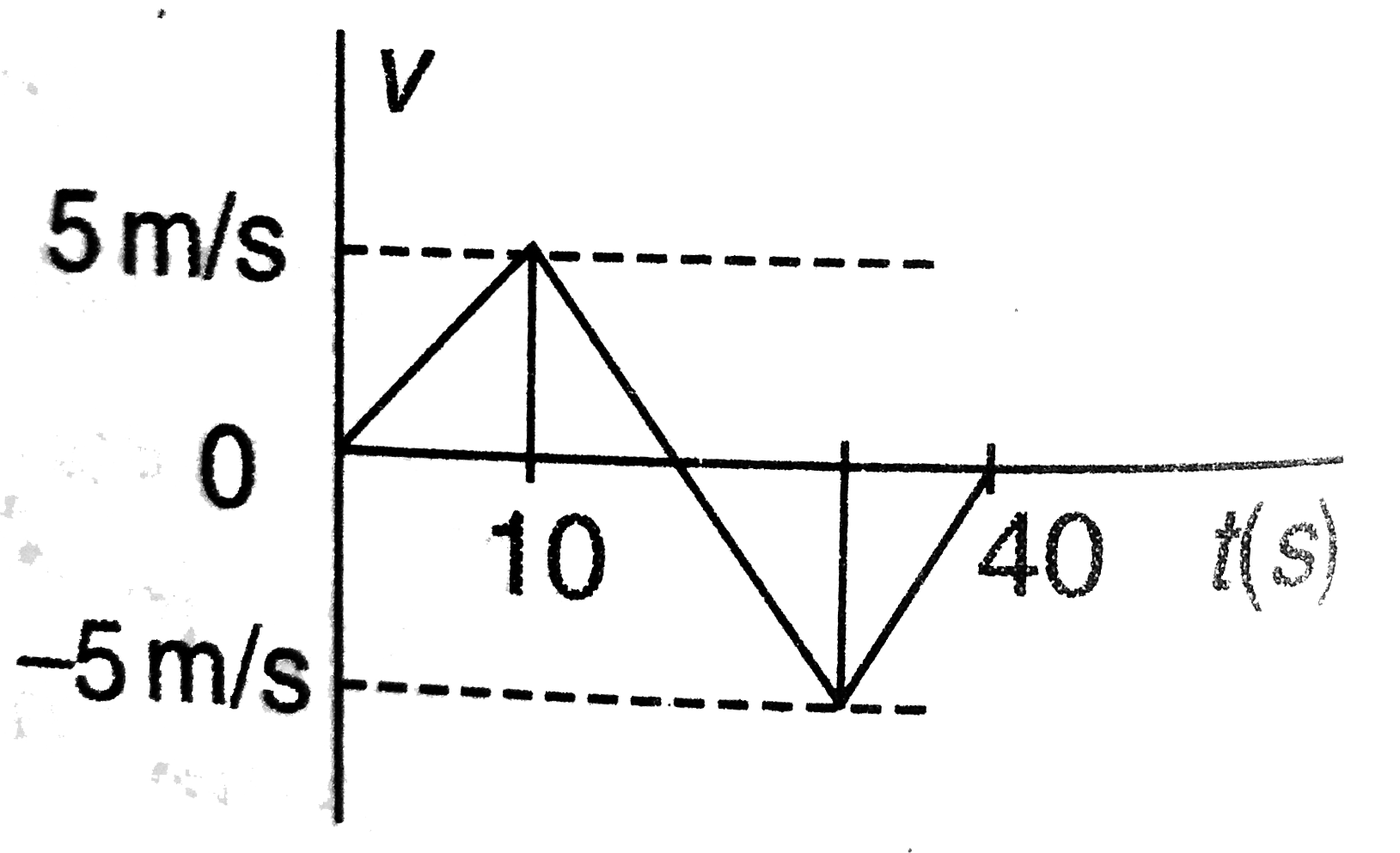AzeroB2.5m/sC5m/sDnoneAssertion: The average velocity of a particle is zero in a time interval. It is possible that the instantaneous acceleration is never zero in the interval.
Reason: The magnitude of average velocity in an interval is equal to its average speed in that interval.AIf both assertion & Reason are True & the Reason is a corrrect explanation of the Asserion.BIf both Assertion & Reason are True but Reason is not correct explanation of the Assertion.CIf Assertion is Trie but the Reason is False.DIf both Assertion & Reason are falseThe velocity-time graph of a particle in one-dimensional motion is shown in the figure. Which of the following formulae is correct for describing the motion of the particle over the time interval t1 to t2?
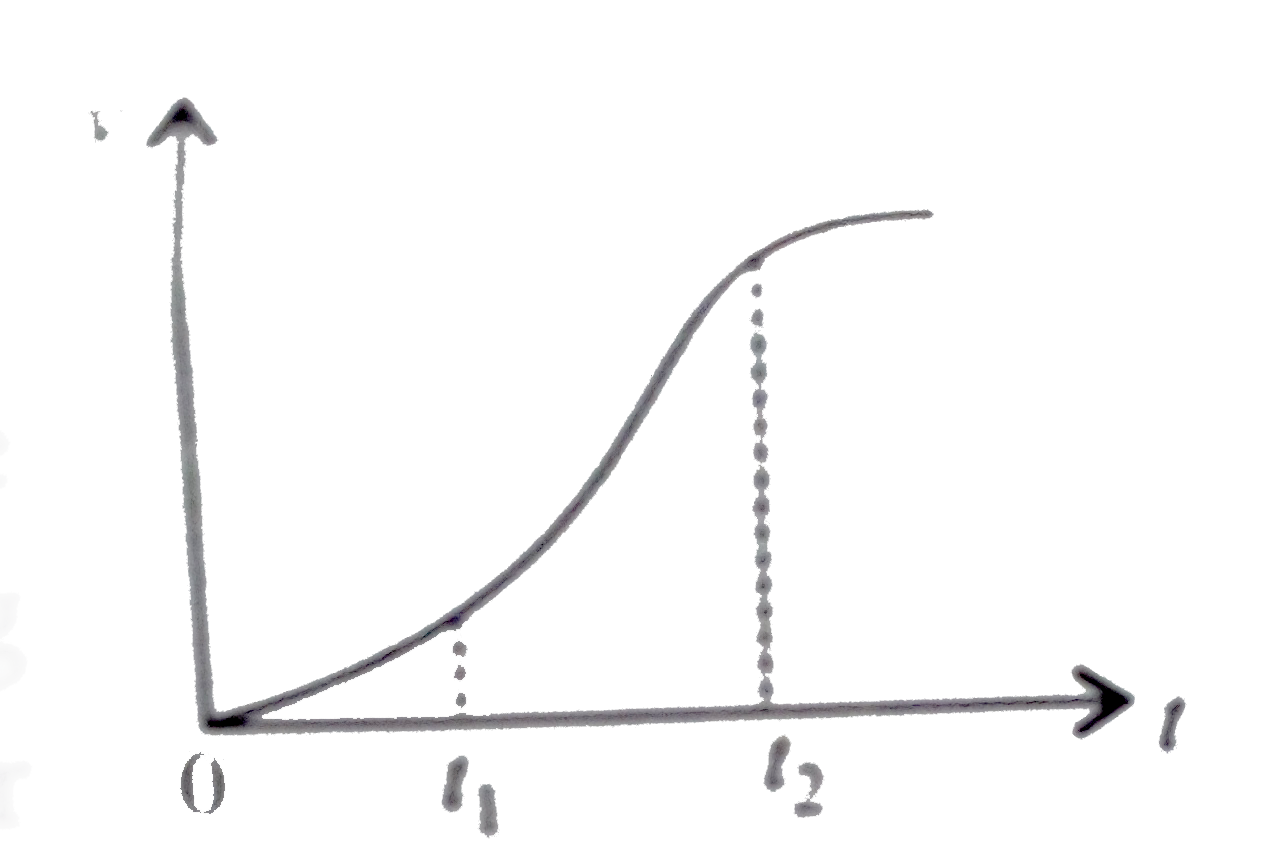Ax(t2)=x(t1)+v(t1)(t2−t1)+(12)a(t2−t1)2Bv(t2)=v(t1)+a(t2−t1)Cvaverage=x(t2)+x(t1)t2−t1Daaverage=v(t2)−v(t1)t2−t1
Figure gives the x-t plot of a particle is one dimensional motion. Give the signs of position, velocity and acceleration of the particle at t = 0.3s
View SolutionFig 2 (NCT).8 gives the x−t plot of a particle executing one dimensional simle harmonic motion. Give the signs of position, velocity and acceleration variables of the particles at t=0.3s, 1.2s,−1.2s,
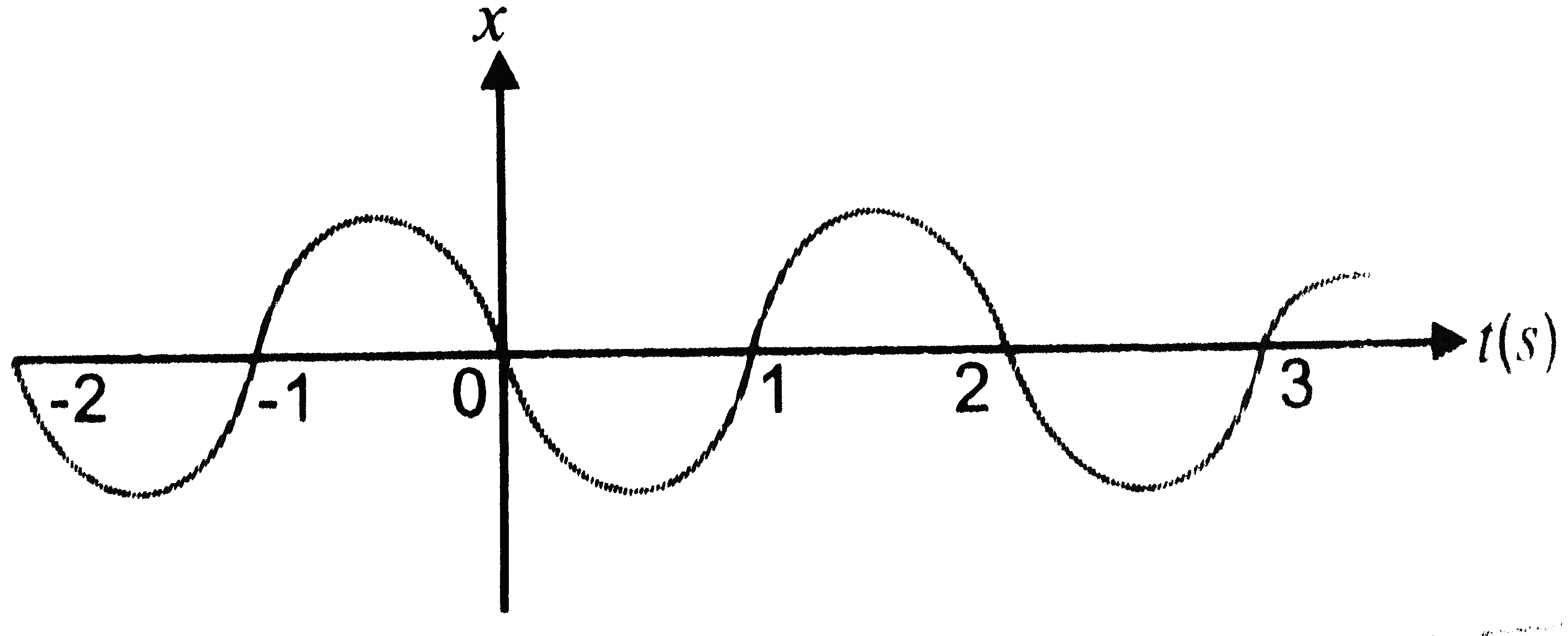
View SolutionFigure shows the x-t plot of a particle moving along a straight line. Let v1 and v2, be average speeds in time intervals 1 and 2 respectively. Then
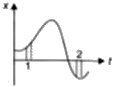
View Solutions-t graph of a particle in motion is shown in Fig. Calculate
Average speed
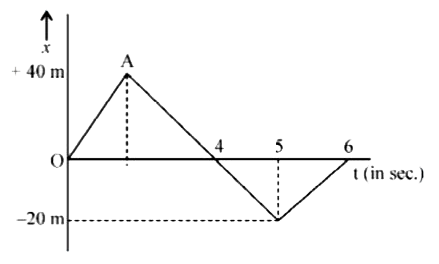
View SolutionFigure shows the velocity of a particle moving on x-axis.
Which of the following statement is correct for the interval shown in graph?
View Solution