Two identical particle each of mass m are inter connects by a light spring of stiffness k ,the time period for small oscillation is equal to
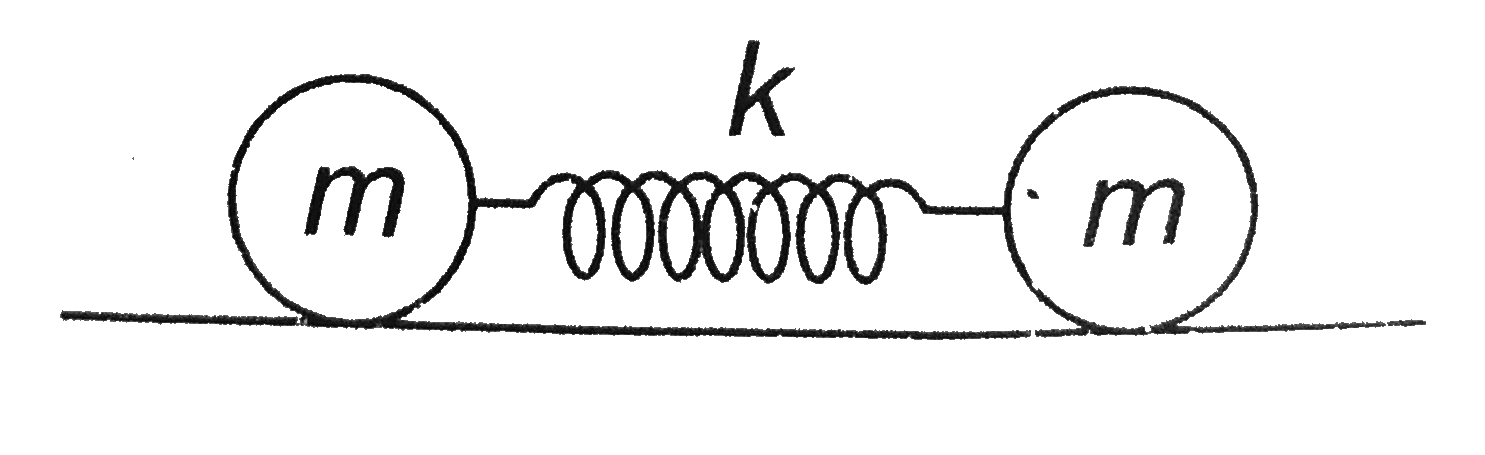
2π√mk
π2√mk
π√m2k
π√2mk
The correct Answer is:D
The reduced mean
μ=(m)(m)m+m=m2
The given system is equavalent to a system at a particle of mass m ? Connected to a spring of stiffness k rigidly.
The requred period of osciltion
T=2π√μk=2π√m/2k
=π√2mk
Topper's Solved these Questions
- OSCILLATION AND SIMPLE HARMONIC MOTIONBook:A2ZChapter:OSCILLATION AND SIMPLE HARMONIC MOTIONExercise:Simple Pendulum And Different Cases Of Shm
Explore 25 Videos
- OSCILLATION AND SIMPLE HARMONIC MOTIONBook:A2ZChapter:OSCILLATION AND SIMPLE HARMONIC MOTIONExercise:Superposition Of Shm And Compound Pendulum
Explore 19 Videos
- OSCILLATION AND SIMPLE HARMONIC MOTIONBook:A2ZChapter:OSCILLATION AND SIMPLE HARMONIC MOTIONExercise:Velocity , Acceleration And Energy Of Simple Harmonic Motion
Explore 40 Videos
- NEWTONS LAWS OF MOTIONBook:A2ZChapter:NEWTONS LAWS OF MOTIONExercise:Chapter Test
Explore 30 Videos
- PROPERTIES OF MATTERBook:A2ZChapter:PROPERTIES OF MATTERExercise:Chapter Test
Explore 29 Videos
Similar Questions
Two identical particles each of mass m are connected by a light spring of stiffness K. The initial deformation of the spring when the system was at rest, x0. After releasing the system, if one of the particles has a speed v and the deformation of the spring is x, find the speed of the other particle neglecting friction.
View SolutionTwo cubes of mass m1 and m2 are interconnected by a weightless spring of stiffness k and placed on a smooth horizontal table. Then the cubes are drawn closer to each other and released. Find the frequency of oscillation.

View Solution
Knowledge Check
Two identical particle each of mass m are inter connects by a light spring of stiffness k ,the time period for small oscillation is equal to
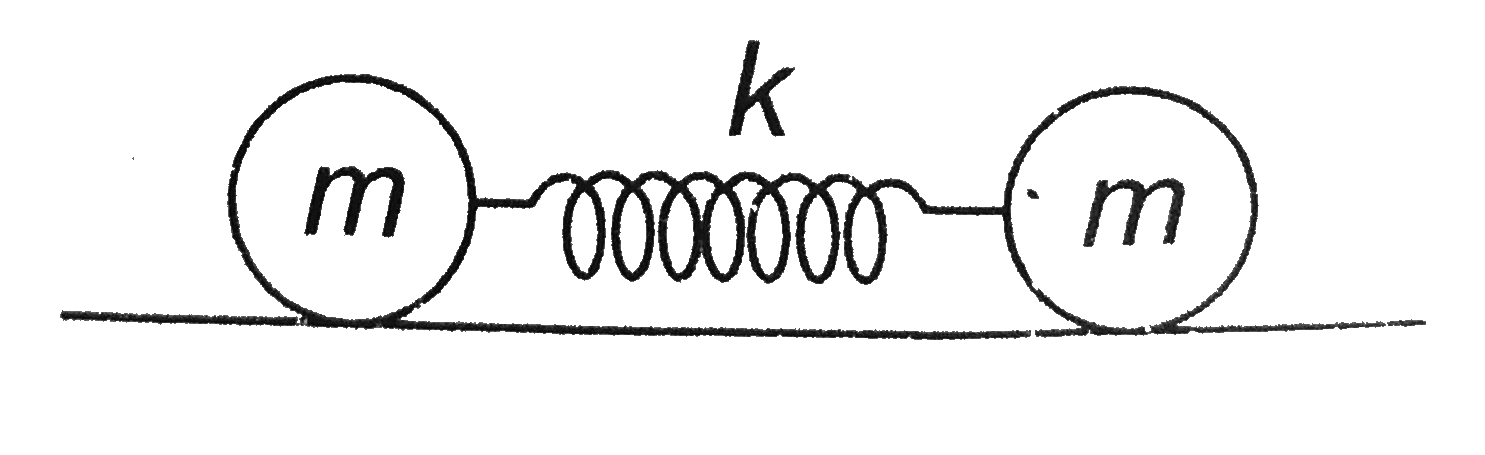 A2π√mkBπ2√mkCπ√m2kDπ√2mk
A2π√mkBπ2√mkCπ√m2kDπ√2mkTwo identical particles each of mass 0.5kg are interconnected by a light springs of stiffness 100N/m, time period of small oscillation is ….
 Aπ5√2Bπ10√2sCπ5sDπ10s
Aπ5√2Bπ10√2sCπ5sDπ10sThe time period of small oscillations of mass m :-
_S01_040_Q01.png) A2π√m6kB2π√11m6KC2π√6m11KD2π√mK
A2π√m6kB2π√11m6KC2π√6m11KD2π√mK
Two identicle particles A and B, each of mass m, are interconnected by a spring of stiffness k. If particle B experiences a forec F and the elongation of the spring is x, the acceleration of particle B relative to particle A is equal to

View SolutionThe following figure shows a particle of mass, m, attached with four identical springs, each of length l. Initial tension in each spring is F0. The period of small oscillations of the particle along a line perpendicular to the plane of the figure is (neglect gravity)

View SolutionA block of mass m is connected to two indentical springs of spring constant k which are in turn connected to fixed supports as shown in the figure. Find the time period for small oscillations of the block.

View SolutionTwo identical blocks A and B , each of mass m resting on smooth floor are connected by a light spring of natural length L and spring constant k, with the spring at its natural length. A third identical block C (mass m) moving with a speed v along the line joining A and B collides with A. The maximum compression in the spring is
View SolutionTwo identical blocks A and B , each of mass m resting on smooth floor are connected by a light spring of natural length L and spring constant k, with the spring at its natural length. A third identical block C (mass m) moving with a speed v along the line joining A and B collides with A. The maximum compression in the spring is
View Solution

