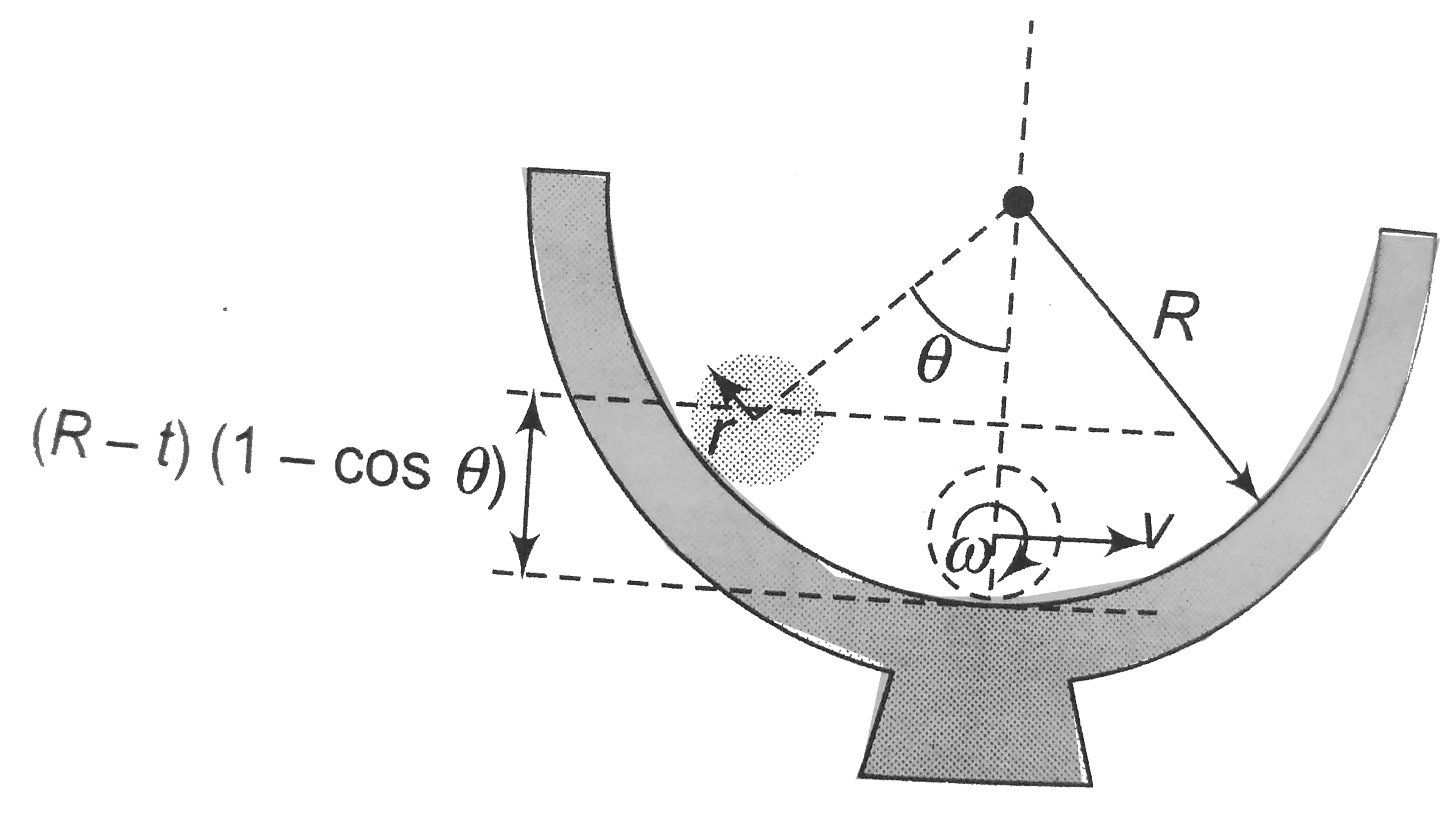
A uniform solid sphere of radius r=R5 is placed on the inside surface of a hemisherical bowl with radius R(=5r). The sphere is released from rest at an angle θ=37∘ to the vertical and rolls without slipping (Fig.) The angular speed of the sphere when it reaches the bottom of the bowl is.
 .
.
The correct Answer is:B
(b) For the isolated sphere-Earth system, energy conserved,
ΔU+ΔKrat+ΔKtrans=0
mg(R−r)(cosθ−1)+[12mv2−0]+12[25mr2]ω2=0
Substituting v=rω we obtain
mg(R−r)(cosθ−1)+[12m(rω)2−0]
+12[25mr2]ω2=0
mg(R−r)(cosθ−1)+[12+15]mr2ω2=0
ω=√(107)(R−r)(1−cosθ)gr2 ...(i)
Here we have r=R5andθ=37∘
Substituting this values in equation (i), we get
ω=√407Rg.
 .
.
Topper's Solved these Questions
- ROTATIONAL DYNAMICSBook:A2ZChapter:ROTATIONAL DYNAMICSExercise:Assertion Reasoning
Explore 20 Videos
- ROTATIONAL DYNAMICSBook:A2ZChapter:ROTATIONAL DYNAMICSExercise:NEET Questions
Explore 59 Videos
- ROTATIONAL DYNAMICSBook:A2ZChapter:ROTATIONAL DYNAMICSExercise:Rotation And Translation Combined And Rolling Motion
Explore 18 Videos
- PROPERTIES OF MATTERBook:A2ZChapter:PROPERTIES OF MATTERExercise:Chapter Test
Explore 29 Videos
- THERMAL PROPERTIES OF MATTERBook:A2ZChapter:THERMAL PROPERTIES OF MATTERExercise:Chapter Test
Explore 30 Videos
Similar Questions
A hollow sphere is released from the top of an inclined plane of inclination θ and length L. If a hollow sphere rolls without slipping, what will be its speed when it reaches the bottom?
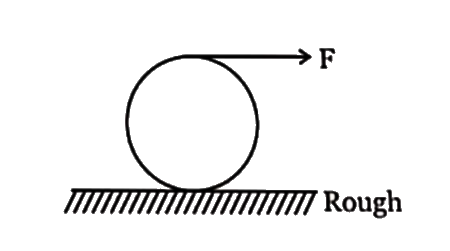
View SolutionA solid sphere of radius R and mass M is rolled by a force F acting at the top of the sphere as shown in the figure. The sphere starts from rest and rolls without slipping, then
View Solution
Knowledge Check
A solid cylinder of mass M and radius R rolls down an inclined plane of height h without slipping. The speed of its centre when it reaches the bottom is.
A√34ghB√43ghC√4ghD√2ghA small sphere S of radius ,r and mass m rolls without slipping, inside a large hemispherical bowl B of radius R as shown in figure. S starts from rest at the top point of the hemisphere
 AThe fraction of translational kinetic energy at the sphere is 5/7.BThe fraction of rotational kinetic energy of the sphere is 2/7.CThe fraction of rotational kinetic energy of the sphere is 27mv2.DThe total kinetic energy of the sphere at the bottom of the bowl is 27mv2
AThe fraction of translational kinetic energy at the sphere is 5/7.BThe fraction of rotational kinetic energy of the sphere is 2/7.CThe fraction of rotational kinetic energy of the sphere is 27mv2.DThe total kinetic energy of the sphere at the bottom of the bowl is 27mv2A small sphere D of mass and radius rols without slipping inside a large fixed hemispherical radius R(>>r) as shown in figure. If the sphere starts from rest at the top point of the hemisphere normal force exerted by the small sphere on the hemisphere when its is at the bottom B of the hemisphere.
 .A107mgB177mgC57mgD75mg
.A107mgB177mgC57mgD75mg
A solid sphere of mass M and radius R is covered with a thin shell of mass M. There is no friction between the inner wall of the shell and the sphere. The ball is released from rest, and then it rolls without slipping down an incline that is inclined at an angle θ to the horizontal. Find the acceleration of the ball.
View Solution
A solid sphere of mass m and radius R is rolling without slipping as shown in figure. Find angular momentum of the sphere about z-axis.
View SolutionA solid sphere rolls down a smooth inclined plane of height h. If it stats from rest then the speed of the sphere when it reaches the bottom is given by
View Solution
A small solid sphere of mass m and radius r starting from rest from the rim of a fixed hemispherical bowl of radius R(>>r) rolls inside it without sliding. The normal reaction exerted by the sphere on the hemisphere when it reaches the bottom of hemisphere is
View SolutionA small solid sphere of radius r rolls down an incline without slipping which ends into a vertical loop of radius R. Find the height above the base so that it just loops the loop
View Solution

