If rod is thrown upward with initial angular velocity and velocity of centre of mass then its momentum changes but angular velocity remains same.
Torque on rod about cente of mass due to gravitational force is zero.

If both assertion and reason are true and reason is the correct explanation of assertion.

If both assertion and reason are reason are true but reason is not the correct explanation of assertion.

If assertion is true but reason is false

If both assertion and reason are false.

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Updated on:21/07/2023

If $' A'$ is areal velocity of a planet of mass $M$ , its angular momentum is
A $M / A$
B $2 M A$
C $A^{2} M$
D $A M^{2}$
A rod is rotating with angular velocity $ω$ about axis AB. Find $cos θ$ .

A $\frac{g}{2 l ω^{2}}$
B $\frac{g}{l ω^{2}}$
C $\frac{2 g}{{(l ω)}^{2}}$
D $\frac{3 g}{2 l ω^{2}}$
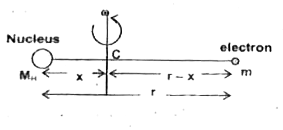
The angular momentum of the atom about the centre of mass will be
A $m r^{2} ω$
B $m {(r - X)}^{2} ω$
C $\frac{(M_{H} + M) r^{2} ω}{M_{H} m^{2}}$
D $\frac{M_{H} m}{M_{H} + m} r^{2} ω$