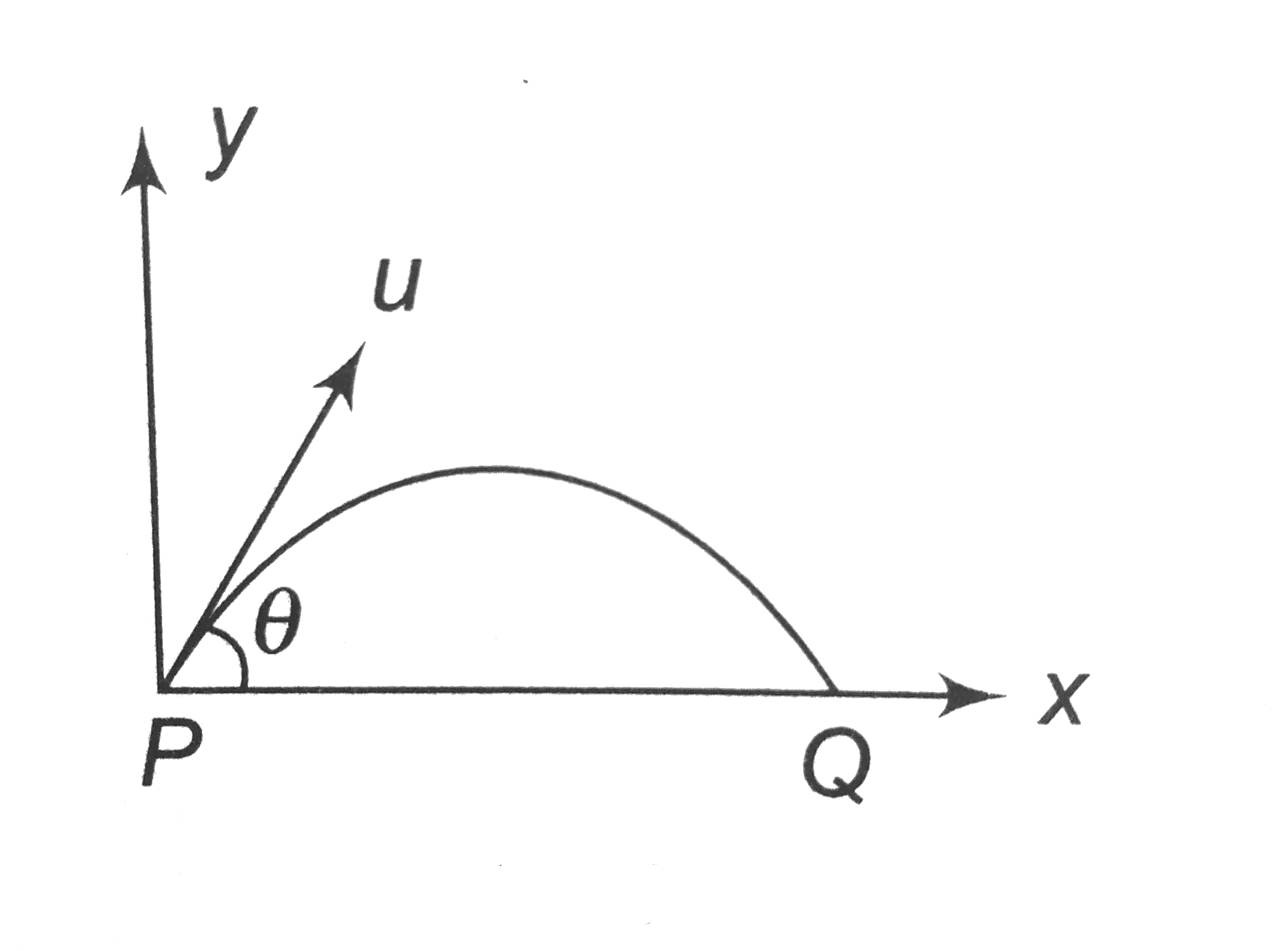
Average torque on a projectile of mass m (initial speed u and angle of projection θ) between initial and final positions P and Q as shown in figure, about the point of projection is :
 .
.
1mu2sin2θ2
mu2cosθ2
mu2sinθ
mu2cosθ
The correct Answer is:A
(a) →τ.Δt=Δ→L…(i)
Here Δt=timeofflight=2usinθg
Change in angular about point of projection (initially it is zero)
∣∣∣−−→ΔL∣∣∣=∣∣→Lf=→Li∣∣=(musinθ) Range
=(musinθ)(u2sin2θ)g=mu2sinθsin2θg
Now |→τav|=∣∣
∣∣−−→ΔLΔt∣∣
∣∣=mu3sinθsin2θg×g2usinθ
=mu2sin2θ2.
Topper's Solved these Questions
- ROTATIONAL DYNAMICSBook:A2ZChapter:ROTATIONAL DYNAMICSExercise:Assertion Reasoning
Explore 20 Videos
- ROTATIONAL DYNAMICSBook:A2ZChapter:ROTATIONAL DYNAMICSExercise:NEET Questions
Explore 59 Videos
- ROTATIONAL DYNAMICSBook:A2ZChapter:ROTATIONAL DYNAMICSExercise:Rotation And Translation Combined And Rolling Motion
Explore 18 Videos
- PROPERTIES OF MATTERBook:A2ZChapter:PROPERTIES OF MATTERExercise:Chapter Test
Explore 29 Videos
- THERMAL PROPERTIES OF MATTERBook:A2ZChapter:THERMAL PROPERTIES OF MATTERExercise:Chapter Test
Explore 30 Videos
Similar Questions
If a projectile has a constant initial speed and angle of projection, find the relation between the chages in the horizontal range due to change in accelertion due to grvity.
View SolutionA particle of mass m is projected with a speed v0 at an angle of projection θ with horizontal. Find the torque of the weight of the particle about the point of projection after time v0sinθg
View Solution
Knowledge Check
A stone is projected with speed u and angle of projection is θ. Find radius of curvature at t=0.
Au2cos2θgBu2gsinθCu2gcosθDu2sin2θgA particle of mass m is thrown with speed u at an angle of projection θ with horizontal. The average power imparted by the gravitational force until it strikes the ground is
AzeroBmgHmaxTCmgHmax2TD2mgHmaxTA particle of mass m is projected with an initial velocity U at an angle θ to the horizontal. The torque of gravity on projectile at maximum height about the point of projection is
AmU2Sin2θ2BmU2Sin2θCmU2Sinθ2D12mU2(Sin2θ)2
The speed of a projectile at its maximum height is half of its initial speed. The angle of projection is .
View SolutionA particle of mass m is projected with a speed u at an angle θ with the horizontal. Find angular momentum of particle after time t about point of projection.
View SolutionA particle of mass m is projected from the ground with an initial speed u at an angle α. Find the magnitude of its angular momentum at the highest point of its trajector about the point of projection.
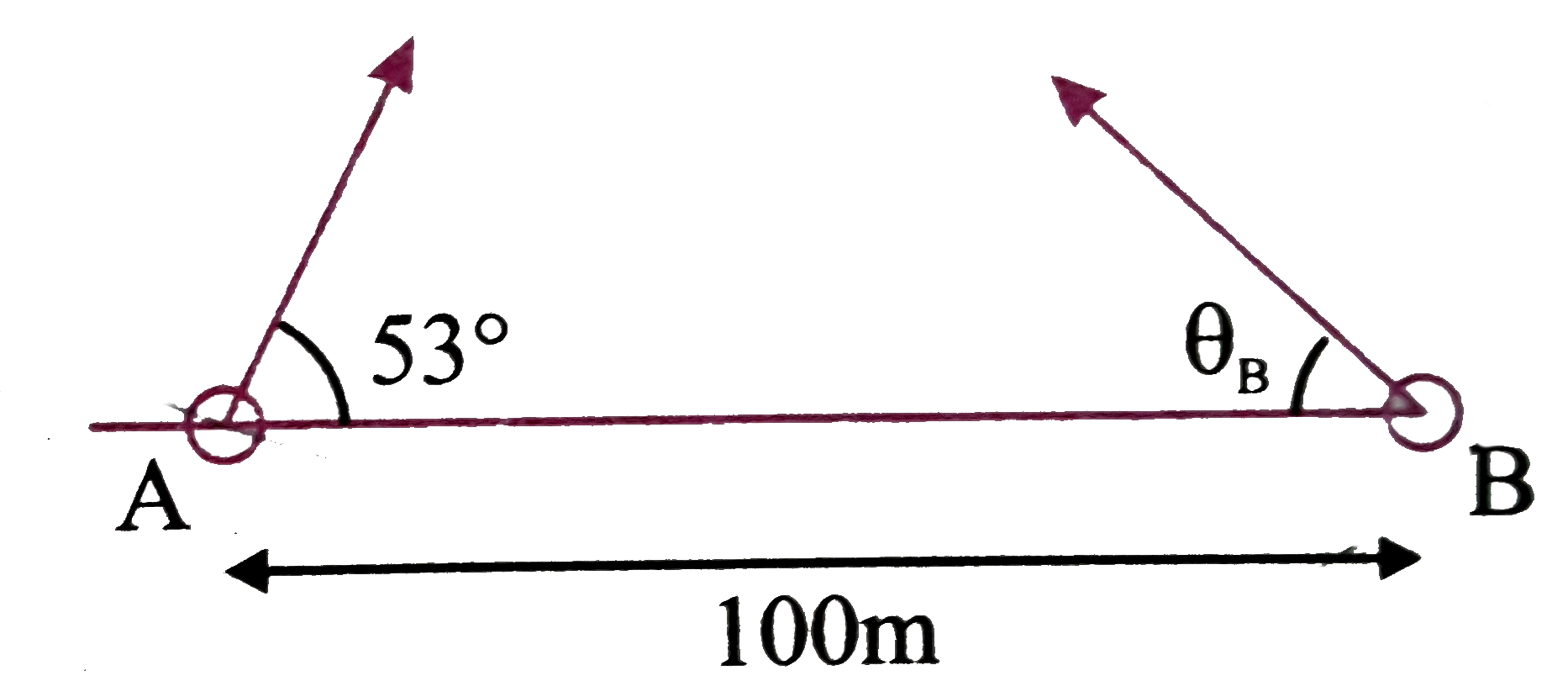
View SolutionTwo particles A and B are projected in same vertical plane as shown in figure.Their initial positions (t=0), initial spped and angle of projections are indicated in the diagram.If initial angle of projection θB=37∘, what should be initial speed of projection of particle B, so that it hits particle A.UA=60m/s
View SolutionA projectile thrown with an initial speed u and the angle of projection 15∘ to the horizontal has a range R. If the same projectile is thrown at an angle of 45∘ to the horizontal with speed 2u, what will be its range ?
View Solution

