A track is mounted on a large wheel that is free to turn with neigligible friction about a vertical axis (Fig). A toy train of mass M is placed on the track and, with the system initially at rest, the train's electrical power is turned on. The train reaches speed v with respect to the track. What is the wheel's angular speed if its mass is m and its radius is r ? (Treat it as a hoop, and neglect the mass of the spokes and hub).
 .
.
v(M/m+1)R
v(m/M+2)R
v(M/m+2)R
v(m/M+2)R
The correct Answer is:B
(b) No external torque acts on the system consisting of the train and wheel, so the total angular momentum of the system (which is initially zero) remains zero.
Let I=mR2 be the rotational inertia of the wheel (which we treat as a hoop). Its angular momentum is
→Lwheel=(Iω)ˆk=−mR2|ω|ˆk
Where ˆk is up in figure and that last step (with the minus sign) is done in recognition that the wheel's clockwise rotation implies a negative vlaue for ω. The linear speed of point on the track is −|ω|R and the speed of the train (going counterclockwise in figure with the speed v' relative to an outside observer) is therefore v'=v−|ω|R where v is its speed relative to the tracks. Consequently, the angular momentum of the train is →Ltra∈=M(v−|ω|R)Rˆk. Conservation of angular momentum yields.
0=→Lwheel+→Ltrain=−mR2|ω|ˆk+M(v−|ω|R)Rˆk
which we can use to solve for |ω|
Solving for the angular speed, the result is
|ω|=mvR(M+m)R2=v(m/M+1)R.]
Topper's Solved these Questions
- ROTATIONAL DYNAMICSBook:A2ZChapter:ROTATIONAL DYNAMICSExercise:Assertion Reasoning
Explore 20 Videos
- ROTATIONAL DYNAMICSBook:A2ZChapter:ROTATIONAL DYNAMICSExercise:NEET Questions
Explore 59 Videos
- ROTATIONAL DYNAMICSBook:A2ZChapter:ROTATIONAL DYNAMICSExercise:Rotation And Translation Combined And Rolling Motion
Explore 18 Videos
- PROPERTIES OF MATTERBook:A2ZChapter:PROPERTIES OF MATTERExercise:Chapter Test
Explore 29 Videos
- THERMAL PROPERTIES OF MATTERBook:A2ZChapter:THERMAL PROPERTIES OF MATTERExercise:Chapter Test
Explore 30 Videos
Similar Questions
Two trains are moving with equal speed in opposite directions along two parallel railway tracks. If the wind is blowing with speed u along the track so that the relative velocities of the trains with respect to the wind are in the ratio 1:2, then the speed of each train must be
View SolutionA train of mass M is moving on a circular track of radius R with constant speed v. The length of the train is half of the perimeter of the track. The linear momentum of the train will be
View Solution
Knowledge Check
A train of mass M is moving on a circular track of radius R with constant speed v. The length of the train is half of the perimeter of the track. The linear momentum of the train will be
AzeroB2MvπCMVRDMVHigh-speed magnetic levitation trains run without touching the track, on the power of
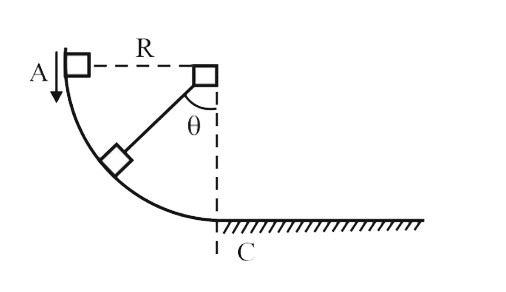
AelectromagnetsBbar magnetsCnatural magnetsDnone of theseA block of mass m is placed on a circular track and then it is given a velocity υ vertically downwards at position A on track. If block moves on track with constant speed, then
 ACoefficient of friction between block and circular track as function of angle θ is μ=sinθcotθ+v2RgBCoefficient of friction between block and circular track as function of angle θ is μ=sinθcosθ+v2RgCInstantaneous power due to friction is −mgvsinθDWork done from A to C by friction on block will be −mgR
ACoefficient of friction between block and circular track as function of angle θ is μ=sinθcotθ+v2RgBCoefficient of friction between block and circular track as function of angle θ is μ=sinθcosθ+v2RgCInstantaneous power due to friction is −mgvsinθDWork done from A to C by friction on block will be −mgR
A train of mass m moves with a velocity υ on the equator from east to west. If ω is the angular speed of earth about its axis and R is the radius of the earth then the normal reaction acting on the train is
View SolutionA block of mass m is placed on a vertical fixed circular track and then it is given velocity v along the track at position A on track. The coefficient of friction between the block and the track varies with the angle θ . If the block moves on track with constant speed then the coefficient of friction is
View SolutionTwo trains start from a certain place on two parallel tracks in the same direction. The speed of the trains are 45km/hr and 40km/hr respectively. The distance between the two trains after 45 minutes will be
View SolutionA train is running at a constant speed of 90 km/h on a straight track. A person standing at the top of a boggey moves in the direction of motion of the train such that he covers 1 meters on the train each second. The speed of the person with respect to ground to -
View SolutionA train of 150 m length is going towards North at a speed of 10 m/s. A bird is flying at 5 m/s parallel to the track towards South. The time taken by the bird to corss the train is
View Solution

