A body is moving from rest under constant acceleration and let S1 be the displacement in the first (p−1) sec and S2 be the displacement in the first p sec. The displacement in (p2−p+1) sec. will be
S1+S2
S1S2
S1−S2
S1/S2
The correct Answer is:A
To solve the problem, we need to find the displacement of a body moving from rest under constant acceleration for a specific time interval. Let's break down the steps:
Step 1: Understand the given information
- The body starts from rest, so the initial velocity u=0.
- The acceleration is constant, denoted as a.
- We need to find the displacement in the time interval of (p2−p+1) seconds.
Step 2: Calculate the displacement in the first (p−1) seconds
Using the formula for displacement under constant acceleration:
S1=ut+12at2
For t=(p−1):
S1=0⋅(p−1)+12a(p−1)2=12a(p−1)2
Step 3: Calculate the displacement in the first p seconds
Using the same formula:
S2=ut+12at2
For t=p:
S2=0⋅p+12ap2=12ap2
Step 4: Calculate the total displacement in (p2−p+1) seconds
Using the displacement formula again:
S=ut+12at2
For t=(p2−p+1):
S=0⋅(p2−p+1)+12a(p2−p+1)2
Step 5: Expand (p2−p+1)2
(p2−p+1)2=(p2−p+1)(p2−p+1)=p4−2p3+3p2−2p+1
Thus,
S=12a(p4−2p3+3p2−2p+1)
Step 6: Relate S to S1 and S2
We know that:
S=S1+S2
Substituting the values of S1 and S2:
S=12a(p−1)2+12ap2
Now, simplifying S1+S2:
S1+S2=12a((p−1)2+p2)
Calculating (p−1)2+p2:
(p−1)2+p2=(p2−2p+1)+p2=2p2−2p+1
Thus,
S1+S2=12a(2p2−2p+1)
Final Result
From the above calculations, we can conclude that:
S=S1+S2
Thus, the displacement in (p2−p+1) seconds is:
S=S1+S2
Conclusion
The displacement in (p2−p+1) seconds is equal to S1+S2.
---
- The body starts from rest, so the initial velocity u=0.
- The acceleration is constant, denoted as a.
- We need to find the displacement in the time interval of (p2−p+1) seconds.
Using the formula for displacement under constant acceleration:
S1=ut+12at2
For t=(p−1):
S1=0⋅(p−1)+12a(p−1)2=12a(p−1)2
Using the same formula:
S2=ut+12at2
For t=p:
S2=0⋅p+12ap2=12ap2
Using the displacement formula again:
S=ut+12at2
For t=(p2−p+1):
S=0⋅(p2−p+1)+12a(p2−p+1)2
(p2−p+1)2=(p2−p+1)(p2−p+1)=p4−2p3+3p2−2p+1
Thus,
S=12a(p4−2p3+3p2−2p+1)
We know that:
S=S1+S2
Substituting the values of S1 and S2:
S=12a(p−1)2+12ap2
Now, simplifying S1+S2:
S1+S2=12a((p−1)2+p2)
Calculating (p−1)2+p2:
(p−1)2+p2=(p2−2p+1)+p2=2p2−2p+1
Thus,
S1+S2=12a(2p2−2p+1)
From the above calculations, we can conclude that:
S=S1+S2
Thus, the displacement in (p2−p+1) seconds is:
S=S1+S2
The displacement in (p2−p+1) seconds is equal to S1+S2.
Topper's Solved these Questions
- GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONBook:A2ZChapter:GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONExercise:AIIMS Questions
Explore 20 Videos
- FLUID MECHANICSBook:A2ZChapter:FLUID MECHANICSExercise:Chapter Test
Explore 29 Videos
- GRAVITATIONBook:A2ZChapter:GRAVITATIONExercise:Chapter Test
Explore 29 Videos
Similar Questions
A particle starts moving from rest under uniform acceleration.It travels a distance x in the first 2 sec and a distance in the next 2sec.If u=nx then n is
View SolutionA body is moving from rest under constance accelration and let S1 be the displacement in the first (p−1) sec and S2 be the displacement in the first p sec. The displacement in (p2−p+1)th sec will be
View Solution
Knowledge Check
A body is moving from rest under constance accelration and let S1 be the displacement in the first (p−1) sec and S2 be the displacement in the first p sec. The displacement in (p2−p+1)th sec will be
AS1+S2BS1S2CS1−S2DS1S2A particle starts moving from rest under a constant acceleration. It travels a distance x in the first 10 sec and distance y in the next 10 sec, then
Ay = xBy = 2xCy = 3xDy = 4xA particle starts from rest and moves with constant acceleration. Then velocity displacement curve is:
A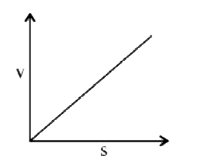 B
B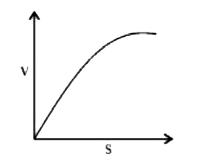 C
C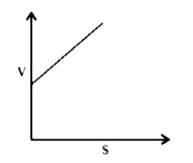 D
D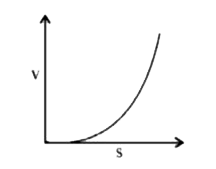
A body moves from rest with a constant acceleration of 5m/s2. Its instantaneous speed (in m/s) at the end of 10 sec is
View SolutionA particle starts moving from the position of rest under a constant acc. It travels a distance x in the first 10 sec and distance y in the next 10 sec, then:
View SolutionIn the above question, the displacement of particle at t = 1 sec and x = 4 cm is:
View SolutionA particle is moving under constant acceleration a=kt. The motion starts from rest. The velocity and displacement as a function of time t is
View SolutionA particle experiences a constant acceleration for 20 sec after starting from rest. If it travels distance S1 in the first 10 sec and a distance S2 in the next 10 sec, Then
View Solution

