A longitudinal standing wave y=acoskxcosωt is maintained in a homogeneious medium of density ρ. Here ω is the angular speed and k , the wave number and a is the amplitude of the standing wave . This standing wave exists all over a given region of space.
The space density of the potential energy PE=Ep(x,t) at a point (x,t) in this space is
Ep=ρa2ω22
Ep=ρa2ω22cos2kxsin2ωt
Ep=ρa2ω22sin2kxcos2ωt
Ep=ρa2ω22sin2kxsin2ωt
The correct Answer is:C
The given longitudinal standing wave is
y=acoskxcosωt (i)
The nodes of this wave are located where coskx=0 (i.e., ) at the values
x=λ4,3λ4,…
and the antinodes are located where coskx=±(i.e.,) at the values
x=0,λ2,...
At the nodes , the space density of kinetic energy ( kinetic energy per unit vanishes for the nodes , i.e.,
x=λ4,3λ4etc.
Also , y is maximum at t=0 , as we see from Eq.(i). Hence potential energy must be maximum at t=0 . Hence the time factor in potential energy density must enter as cos2ωt. Also , the sum of kinetic and potential energy densities must always be constant for a given x as it represents total energy at that point.
Hence the potential energy density is
Ep=ρa2ω22sin2kxcos2ωt (ii)
and the kinetic energy density is
Ek=ρa2ω22cos2kxsin2ωt (iii)
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Integer9videos
SUPERPOSITION AND STANDING WAVES
- BOOK - CENGAGE PHYSICSCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Multiple Correct Answers Type5videos
SUPERPOSITION AND STANDING WAVES
- BOOK - CENGAGE PHYSICSCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Assertion - Reasoning6videos
SUPERPOSITION AND STANDING WAVES
- BOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
- BOOK - CENGAGE PHYSICSCHAPTER - THERMODYNAMICSEXERCISE - 241videos
THERMODYNAMICS
Similar Questions
Knowledge Check
- Question 1 - Select One
A longitudinal standing wave y=acoskxcosωt is maintained in a homogeneious medium of density ρ. Here ω is the angular speed and k , the wave number and a is the amplitude of the standing wave . This standing wave exists all over a given region of space.
The space density of the kinetic energy . KE=Ek(x,t) at the point (x,t) is given byAEk=ρa2ω22cos2kxcos2ωtBEk=ρa2ω22sin2kxcos2ωtCEk=ρa2ω22DEk=ρa2ω22cos2kxsin2ωt - Question 2 - Select One
A longitudinal standing wave y=acoskxcosωt is maintained in a homogeneious medium of density ρ. Here ω is the angular speed and k , the wave number and a is the amplitude of the standing wave . This standing wave exists all over a given region of space.
If a graph E(=Ep+Ek) versus t , i.e., total space energy density verus time were drawn at the instants of time t=0 and t=T/4, between two successive nodes separated by distance λ/2 which of the following graphs correctly shows the total energy (E) distribution at the two instants.A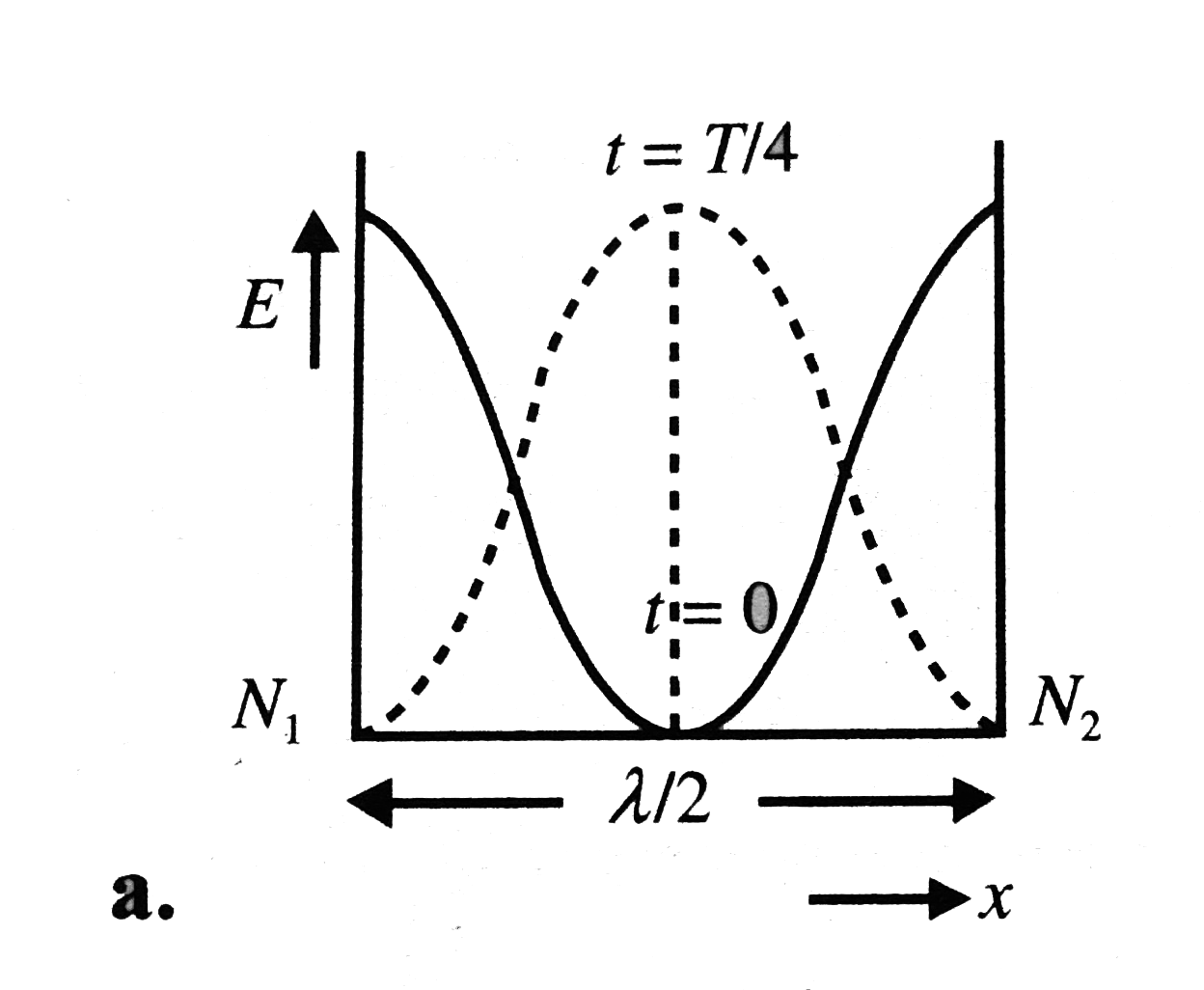 B
B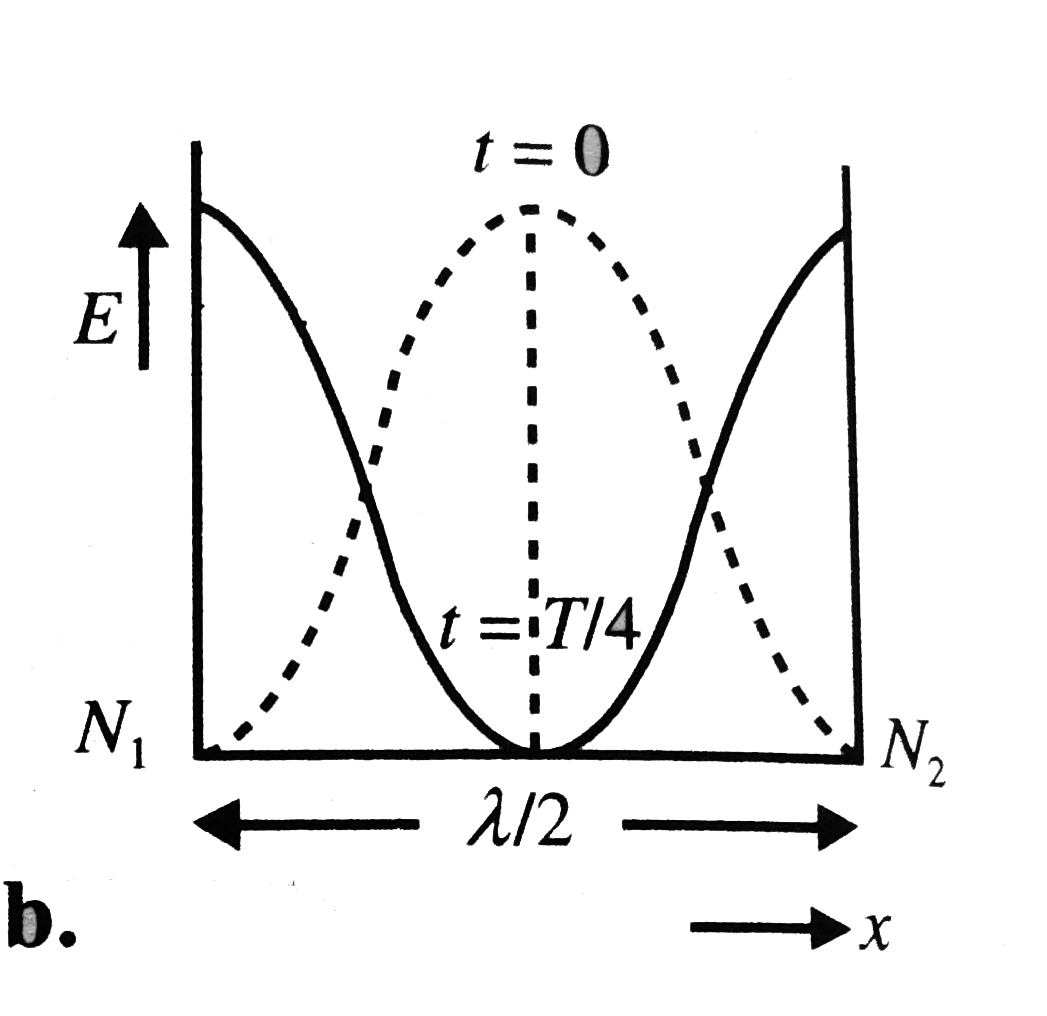 C
C D
D
Standing Waves
View SolutionStanding Waves
View SolutionFind out the equation of the standing waves for the following standing wave pattern.
 View Solution
View SolutionEnergy OF travelling & standing waves
View SolutionA longitudinal standing wave ξacoskx.Cosωt is maintained in a homogeneous medium of density ρ. Find the expressions for the space density of
(a) potential energy wp(x,t),
(b) kinetic energy wk(x,t),
Plot the space density distribution of the total energy w in the space between the displacement nodes at the moments t=0 and t=T/4, where T is oscillation period.View SolutionA standing wave ξ=asinkx.Cosωt is maintained in a homogeneous rod with cross − sectional area S and density ρ. Find the total mechanical energy confined between the sections corresponding to the adjacent displacement nodes.
View Solution

