A longitudinal standing wave $ξ a cos k x . Cos ω t$ is maintained in a homogeneous medium of density $ρ$ . Find the expressions for the space density of
$(a)$ potential energy $w_{p} (x, t),$
$(b)$ kinetic energy $w_{k} (x, t),$
Plot the space density distribution of the total energy $w$ in the space between the displacement nodes at the moments $t = 0$ and $t = T / 4$ , where $T$ is oscillation period.

Video Solution

Text Solution

Verified by Experts

Given $ξ = a cos k x cos ω t$
$(a)$ The potential energy density $($ per unit volume $)$ is the energy of longitudinal strain. This is
$w_{p} = (\frac{1}{2} stress \times strain) = \frac{1}{2} E {(\frac{δ ξ}{δ x})}^{2}, (\frac{δ ξ}{δ x}$ is longitudinal strain )
$w_{p} = \frac{1}{2} E a^{2} k^{2} {sin}^{2} k x {cos}^{2} ω t$
But $\frac{ω^{2}}{k^{2}} = \frac{E}{ρ}$ or $E k^{2} = ρ ω^{2}$
Thus $w_{p} = \frac{1}{2} ρ a^{2} ω^{2} {sin}^{2} k x {cos}^{2} ω t$
$(b)$ The kinetic energy density is
$= \frac{1}{2} ρ (\frac{δ ξ}{δ t}) = \frac{1}{2} ρ a^{2} ω^{2} {cos}^{2} k x {sin}^{2} ω t$ .
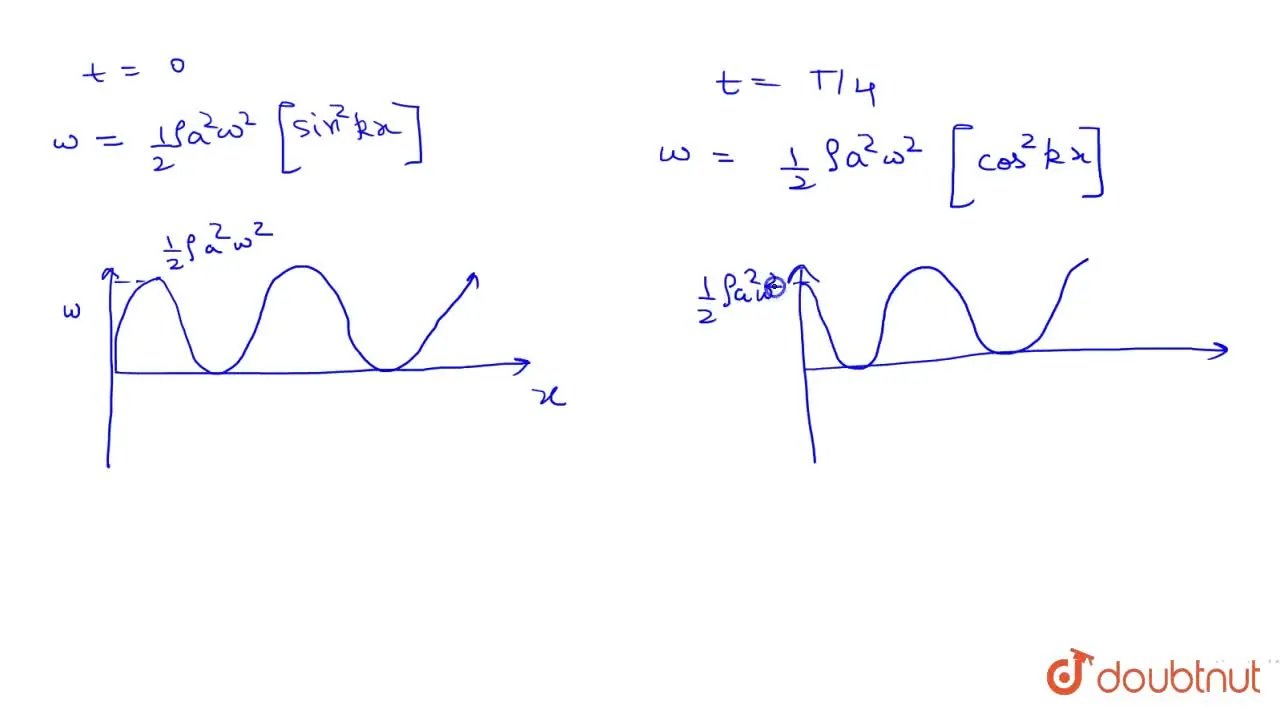
On plotting we get figure given in the book $(p .332)$ . For example at $t = 0$
$w = w_{p} + w_{k} = \frac{1}{2} ρ a^{2} ω^{2} {sin}^{2} k x$
and the displacement node are at $x = \pm \frac{π}{2 k}$ so we do get the figure.

Updated on:21/07/2023

A longitudinal standing wave $y = a cos k x cos ω t$ is maintained in a homogeneious medium of density $ρ$ . Here $ω$ is the angular speed and $k$ , the wave number and $a$ is the amplitude of the standing wave . This standing wave exists all over a given region of space.
The space density of the potential energy $P E = E_{p} (x, t)$ at a point $(x, t)$ in this space is
A $E_{p} = \frac{ρ a^{2} ω^{2}}{2}$
B $E_{p} = \frac{ρ a^{2} ω^{2}}{2} {cos}^{2} k x {sin}^{2} ω t$
C $E_{p} = \frac{ρ a^{2} ω^{2}}{2} {sin}^{2} k x {cos}^{2} ω t$
D $E_{p} = \frac{ρ a^{2} ω^{2}}{2} {sin}^{2} k x {sin}^{2} ω t$
A longitudinal standing wave $y = a cos k x cos ω t$ is maintained in a homogeneious medium of density $ρ$ . Here $ω$ is the angular speed and $k$ , the wave number and $a$ is the amplitude of the standing wave . This standing wave exists all over a given region of space.
The space density of the kinetic energy . $K E = E_{k} (x, t)$ at the point $(x, t)$ is given by
A $E_{k} = \frac{ρ a^{2} ω^{2}}{2} {cos}^{2} k x {cos}^{2} ω t$
B $E_{k} = \frac{ρ a^{2} ω^{2}}{2} {sin}^{2} k x {cos}^{2} ω t$
C $E_{k} = \frac{ρ a^{2} ω^{2}}{2}$
D $E_{k} = \frac{ρ a^{2} ω^{2}}{2} {cos}^{2} k x {sin}^{2} ω t$
A sound wave $y = A sin (ω t - k x)$ is propagating through a medium of density $' ρ'$ . Then the sound energy per unit volume is
A $1 / 2 ρ ω^{2} A^{2}$
B $ρ A^{2} ω^{2}$
C $2 ρ A^{2} ω^{2}$
D $4 ρ A^{2} ω^{2}$