A standing wave ξ=asinkx.Cosωt is maintained in a homogeneous rod with cross − sectional area S and density ρ. Find the total mechanical energy confined between the sections corresponding to the adjacent displacement nodes.
We have a standing wave given by the eqaution
ξ=asinkxcosωt
So, δξδt=−asinkxsinωt....(1)
and δξδt=akcoskxcosωt...(2)
The kinetic energy confined in an element of length dx of the rod
dT=12(ρSdx)(δξδt)2=12ρSa2ω2sin2ωtsin2kxdx
So total kinetic energy confined into rod
T=∫dT=12ρSa2ω2sin2ωt∫γ/20sin2(2πλ)xdx
or,T=πSa2ω2ρsin2ωt4k...(3)
The potential energy in the above rod element
dU=∫δU=−∫ξ0Fξdxi, where 'Fξ=(ρSdx)δ2ξδt2
or, Fξ=(ρSdx)ω2ξ
so, dU=ω2ρSdx∫ξ0ξdxi
or, dU=ρω2Sξ22dx=ρω2Sa2cos2ωtsin2kxdx2
Thus the total potential energy stored in the rod U=∫dU
or,U=ρω2Sa2cos2ωt∫γ/20sin2(2πλ)xdx
So, U=πρSa2ω2cos2ωt4k
To find the potential energy stored in the rod element we may adopt an easier way . We know that the potential energy dencity confined in a rod under elastic force equals :
UD=12 ( stress × straing ) =12σε=12Yε2
=12ρv2ε2=12ρω2k2ε2
=12ρω2k2(δξδx)2=12ρa2ω2cos2ωtcos2kx
Hence the total potential energy stored in the rod
U=∫UDdV=∫γ/2012ρ2ω2cos2ωtcos2kxSdx
=πρSa2ω2cos2ωt4k(4)
Hence the sought mechanical energy confined in the rod between the two adjacent nodes
E=T+U=πρω2a2S4k
Topper's Solved these Questions
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electric Oscillations
56 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Exercise
2 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics
49 Videos
Similar Questions
A longitudinal standing wave ξacoskx.Cosωt is maintained in a homogeneous medium of density ρ. Find the expressions for the space density of
(a) potential energy wp(x,t),
(b) kinetic energy wk(x,t),
Plot the space density distribution of the total energy w in the space between the displacement nodes at the moments t=0 and t=T/4, where T is oscillation period.
View SolutionA plane elastic wave ξ=ae−γxcos(ωt−kx), wherea,γ,ω, and k are constants , propagates in a homogeneous medium. Find the phase difference between the oscillations at the points where the particles, displacement amplitudes differ by η=1.0%, if γ=0.42m−1 and the wavelength is λ=50cm.
View Solution
Knowledge Check
A standing wave is maintained in a homogeneous string of corss-sectional area 'S' and density phe. It is formed by the superposition of two waves travelling in opposite directions given by the equation y1=asin(ωt=kx)andy2=2asin(ωt+kx). The total mechanical energy confined between the sections corresponding to the abjacent antinodes is:
A3πspω2a22kBπspω2a22kC5πspω2a22kD2πspω2a22kA standing wave is maintained in a homogerneous string of cross - sectional area a and density p . It is formed bt yhe superpostions given of two waves travelling in opposite direations given by the equations
A3πspω2a22kBπspω2a22kC5πspω2a22kD2πspω2a22kA longitudinal standing wave y=acoskxcosωt is maintained in a homogeneious medium of density ρ. Here ω is the angular speed and k , the wave number and a is the amplitude of the standing wave . This standing wave exists all over a given region of space.
If a graph E(=Ep+Ek) versus t , i.e., total space energy density verus time were drawn at the instants of time t=0 and t=T/4, between two successive nodes separated by distance λ/2 which of the following graphs correctly shows the total energy (E) distribution at the two instants.A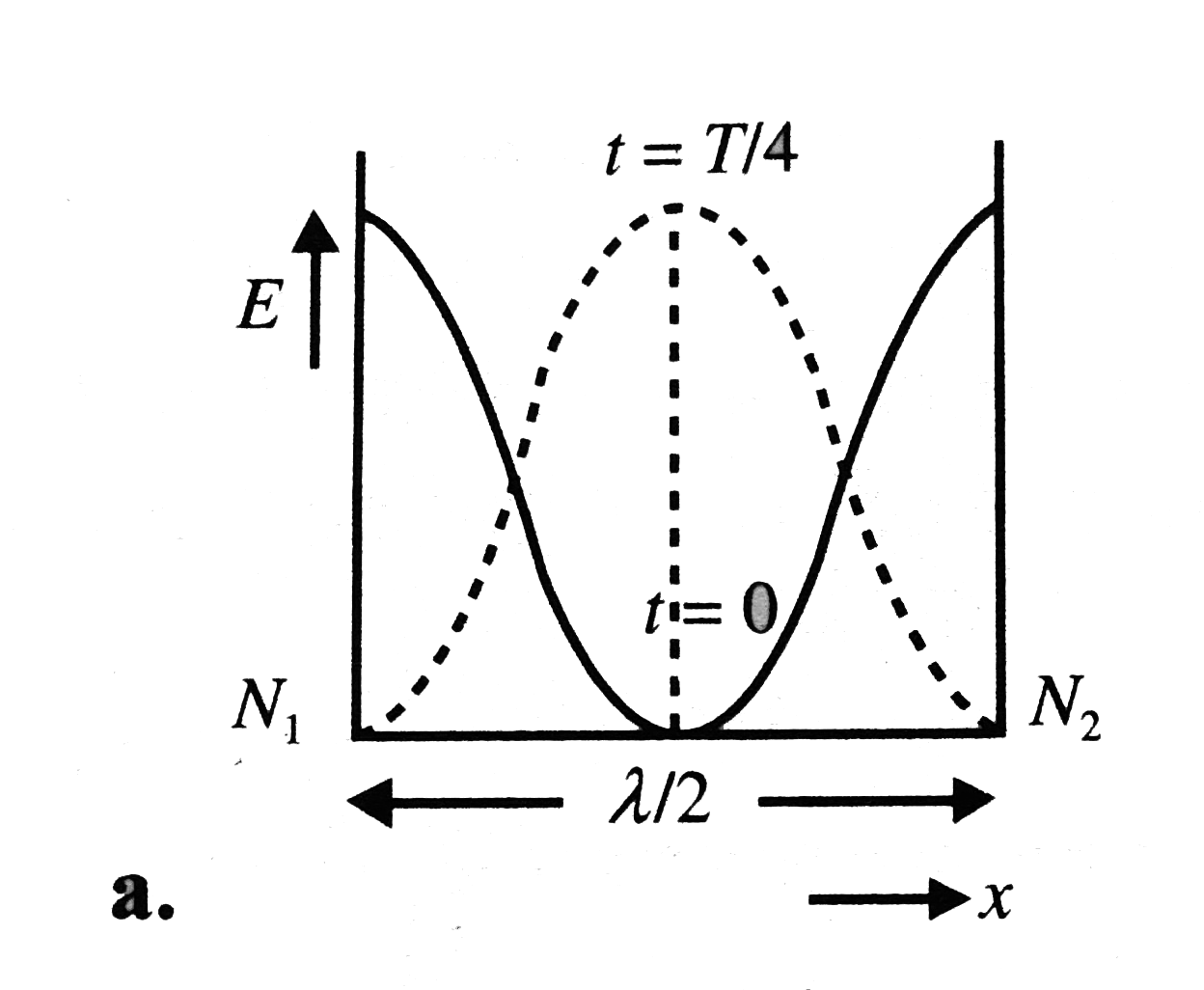 B
B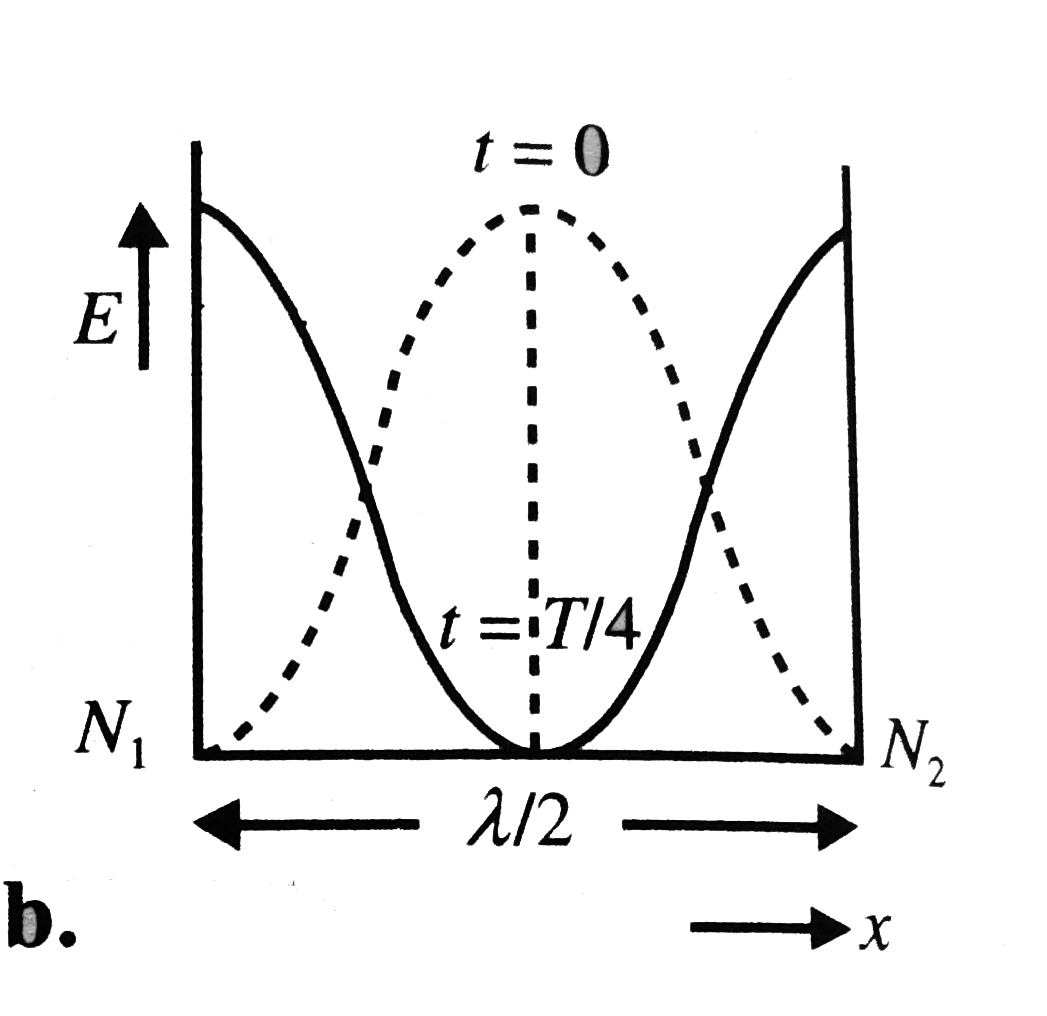 C
C D
D
y1=8sin(ωt−kx)andy2=6sin(ωt+kx) are two waves travelling in a string of area of cross-section s and density rho. These two waves are superimposed to produce a standing wave.
(a) Find the energy of the standing wave between two consecutive nodes.
(b) Find the total amount of energy crossing through a node per second.
View SolutionA standing wave y=Asinkx.cosωt is established in a string fixed at its ends.
(a) What is value of instantaneous power transfer at a cross section of the string when the string is passing through its mean position?
(b) What is value of instantaneous power transfer at a cross section of the string when the string is at its extreme position?
(c) At what frequency is the power transmitted through a cross section changing with time?
View SolutionA transverse wave is passing through a light string shown in fig.The equation of wave is y=Asin(wt−kx) the area of cross-section of string A and density is ρ the hanging mass is
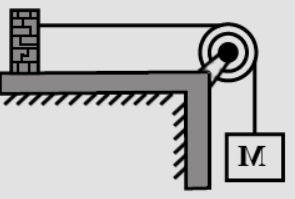
View SolutionA longitudinal standing wave y=acoskxcosωt is maintained in a homogeneious medium of density ρ. Here ω is the angular speed and k , the wave number and a is the amplitude of the standing wave . This standing wave exists all over a given region of space.
The space density of the potential energy PE=Ep(x,t) at a point (x,t) in this space is
View SolutionA longitudinal standing wave y=acoskxcosωt is maintained in a homogeneious medium of density ρ. Here ω is the angular speed and k , the wave number and a is the amplitude of the standing wave . This standing wave exists all over a given region of space.
The space density of the kinetic energy . KE=Ek(x,t) at the point (x,t) is given by
View Solution