A steel rod 2.5m long is rigidly clamped at its centre C and longitudinal waves are set up on both sides of C by rubbing along the rod . Young's modulus for steel =2×1011N/m2 , density of steel =8000kg/m3

If the clamp of the rod be shifted to its end A and totally four antinodes are observed in the rod when longitudinal waves are set up in it , the frequency of vibration of the rod in this mode is
A
500Hz
B
2500Hz
C
3500Hz
D
1500HZ
Video Solution
Text Solution
The correct Answer is:C
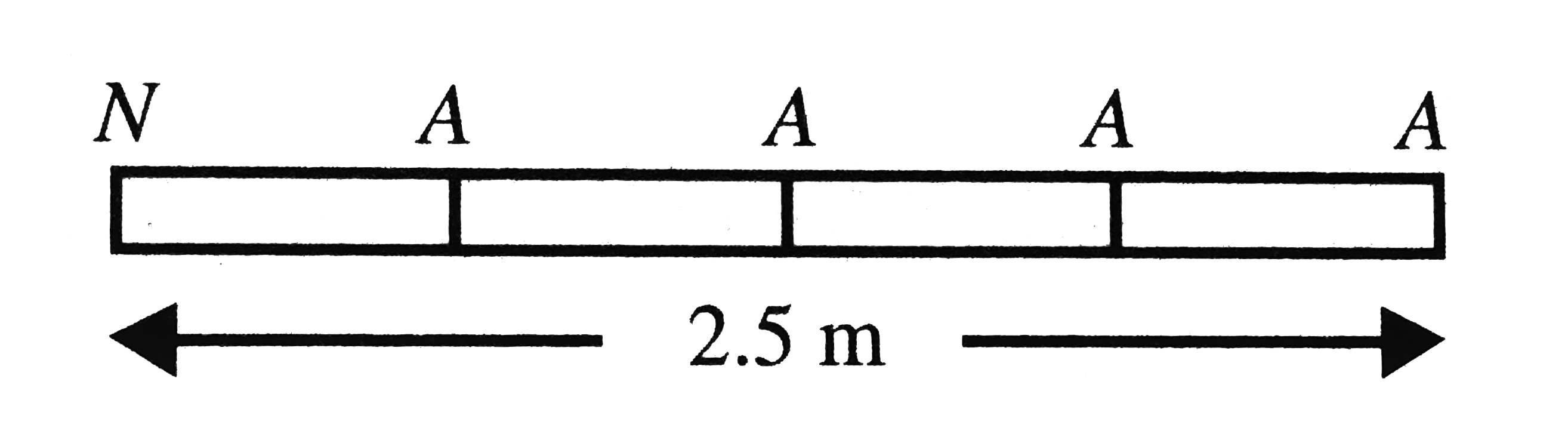
Since the full length of the rod is set into a single mode of vibration in which four antinodes are seen .
Hence if λ be the wavelength for this mode of vibration
We have 3λ2+λ4=2.5
λ=4×2.57=107m
Hence frequency of vibration
=500010/7=3500Hz
|
Topper's Solved these Questions
- SUPERPOSITION AND STANDING WAVESBook:CENGAGE PHYSICSChapter:SUPERPOSITION AND STANDING WAVESExercise:Integer
Explore 9 Videos
- SUPERPOSITION AND STANDING WAVESBook:CENGAGE PHYSICSChapter:SUPERPOSITION AND STANDING WAVESExercise:Multiple Correct Answers Type
Explore 5 Videos
- SUPERPOSITION AND STANDING WAVESBook:CENGAGE PHYSICSChapter:SUPERPOSITION AND STANDING WAVESExercise:Assertion - Reasoning
Explore 6 Videos
- SOUND WAVES AND DOPPLER EFFECTBook:CENGAGE PHYSICSChapter:SOUND WAVES AND DOPPLER EFFECTExercise:Integer
Explore 16 Videos
- THERMODYNAMICSBook:CENGAGE PHYSICSChapter:THERMODYNAMICSExercise:24
Explore 1 Video
Similar Questions
Knowledge Check
A steel rod 2.5m long is rigidly clamped at its centre C and longitudinal waves are set up on both sides of C by rubbing along the rod . Young's modulus for steel =2×1011N/m2 , density of steel =8000kg/m3

If two antinodes are observed on either side of C , the frequency of the node in which the rod is vibrating will beA1000HzB3000HzC7000HzD1500HzA steel rod 2.5m long is rigidly clamped at its centre C and longitudinal waves are set up on both sides of C by rubbing along the rod . Young's modulus for steel =2×1011N/m2 , density of steel =8000kg/m3

If the amplitude of the wave at the antinode , when it is vibrating in its fundamental mode is 2×10−6m , the maximum velocity of a steel particle in its vibration isA1.25×10−2m/sB1.25×10−3m/sC1m/sD0.12m/sIf the young's modulus of the material of the rod is 2×1011N/m2 and its density is 8000kg/m3 then the time taken by a sound wave to traverse 1m of the rod will be
A10−4sB2×10−4sC10−2sD2×10−2s
The Young's modulus of steel is 1.9×1011Nm−2 . Calculate its value in dyne cm−2.
View SolutionCalculate the speed of longitudinal wave in steel. Young's modulus for steel is 3×1010N/m2 and its density 1.2×103kg/m3
View SolutionFor a steel rod, the Young's modulus of elasticity is 2.9×1011N/m2, and the density of steel is 8×103kg/m3.What is the velocity of longitudinal waves in steel?
View SolutionCalculate the speed of longitudinal wave in steel. Young's modulus for steel is 3×1010N/m2 and its density 1.2×103kg/m3
View SolutionWhat is the work done per unit volume when a steel wire is stretched by 0.2% of its original length ? (Young's modulus of steel is 2×1011N/m2)
View Solution

