Consider a standing wave formed on a string . It results due to the superposition of two waves travelling in opposite directions . The waves are travelling along the length of the string in the $x$ - direction and displacements of elements on the string are along the $y$ - direction . Individual equations of the two waves can be expressed as
$Y_{1} = 6 (c m) sin [5 (r a d / c m) x - 4 (r a d / s) t]$
$Y_{2} = 6 (c m) sin [5 (r a d / c m) x + 4 (r a d / s) t]$ Here $x$ and $y$ are in $c m$ .
Answer the following questions.
Maximum value of the $y$ - positions coordinate in the simple harmonic motion of an element of the string that is located at an antinode will be

$\pm 6 c m$

$\pm 8 c m$

$\pm 12 c m$

$\pm 3 c m$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

$y = y_{1} + y_{2} = (12 sin 5 x) cos 4 t$
Maximum value of $y$ - position in $S H M$ of an element of the string that is located at an antinode $= \pm 12 c m (sin 5 x = \pm 1)$
For the position nodes amplitudeshould be zero.
So , $sin 5 x = 0 \Rightarrow 5 x = n π$
$x = \frac{n π}{5}$
where $n = 0, 1, 2, 3, ... . .$
Value of amplitude at $x = 1.8 c m$
$A = 12 sin (5 \times 1.8) = 4.9 c m$
At any instant say $t = 0$ , instantaneous velocity of points on the string is zero for all points as at extreme position velocities of particles are zero.

Updated on:21/07/2023

Class 11 PHYSICS TRAVELLING WAVES

Topper's Solved these Questions

Knowledge Check

Consider a standing wave formed on a string . It results due to the superposition of two waves travelling in opposite directions . The waves are travelling along the length of the string in the $x$ - direction and displacements of elements on the string are along the $y$ - direction . Individual equations of the two waves can be expressed as
$Y_{1} = 6 (c m) sin [5 (r a d / c m) x - 4 (r a d / s) t]$
$Y_{2} = 6 (c m) sin [5 (r a d / c m) x + 4 (r a d / s) t]$ Here $x$ and $y$ are in $c m$ .
Answer the following questions.
If one end of the string is at $x = 0$ , positions of the nodes can be described as
A $x = n π / 5 c m, w h e r e n = 0, 1, 2, \dots$
B $x = n 2 π / 5 c m, w h e r e n = 0, 1, 2, \dots$
C $x = n π / 5 c m, w h e r e n = 0, 1, 3, 5, \dots$
D $x = n π / 10 c m, w h e r e n = 0, 1, 3, 5, \dots$
Consider a standing wave formed on a string . It results due to the superposition of two waves travelling in opposite directions . The waves are travelling along the length of the string in the $x$ - direction and displacements of elements on the string are along the $y$ - direction . Individual equations of the two waves can be expressed as
$Y_{1} = 6 (c m) sin [5 (r a d / c m) x - 4 (r a d / s) t]$
$Y_{2} = 6 (c m) sin [5 (r a d / c m) x + 4 (r a d / s) t]$ Here $x$ and $y$ are in $c m$ .
Answer the following questions.
Amplitude of simple harmonic motion of a point on the string that is located at $x = 1.8 c m$ will be
A $3.3 c m$
B $6.7 c m$
C $4.9 c m$
D $2.6 c m$
Consider a standing wave formed on a string . It results due to the superposition of two waves travelling in opposite directions . The waves are travelling along the length of the string in the $x$ - direction and displacements of elements on the string are along the $y$ - direction . Individual equations of the two waves can be expressed as
$Y_{1} = 6 (c m) sin [5 (r a d / c m) x - 4 (r a d / s) t]$
$Y_{2} = 6 (c m) sin [5 (r a d / c m) x + 4 (r a d / s) t]$ Here $x$ and $y$ are in $c m$ .
Answer the following questions.
Figure 7.104( c) shows the standing wave pattern at $t = 0$ due to superposition of waves given by $y_{1}$ and $y_{2}$ in Figs.7.104(a) and (b) . In Fig. 7.104 (c ) , $N$ is a node and $A$ and antinode . At this instant say $t = 0$ , instantaneous velocity of points on the string

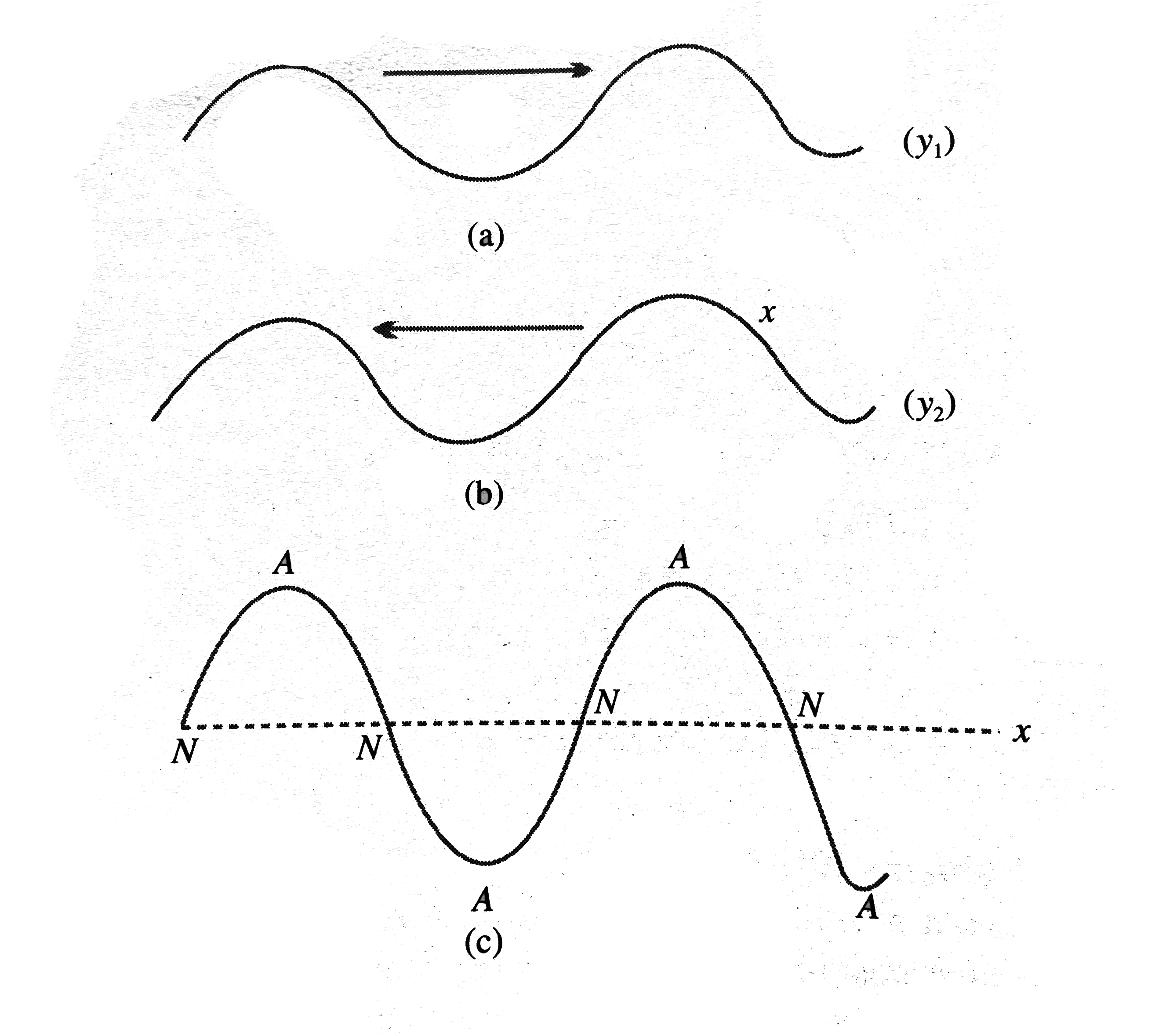Ais different for different points
Bis zero for all points
Cchanges with position of the point
Dis constant but not equal to zero for all points

The correct Answer is:C

Topper's Solved these Questions

Similar Questions

Knowledge Check

CENGAGE PHYSICS-SUPERPOSITION AND STANDING WAVES-Comprehension