Consider the snapshot of a wave traveling in positive x–direction
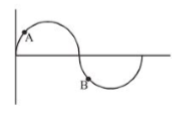
The particle A is moving in –ve y–direction and particle B is moving in +y–direction
The particle B is moving in –ve y–direction and particle A is moving in +y–direction
Both are moving in the +ve y–direction
Both are moving in the –ve y–direction
The correct Answer is:A
VParticle=−(slope)(vwave)
At A : slope →+ve so vp is −ve.
At B : slope →−ve so vp is +ve .
OR
Topper's Solved these Questions
Similar Questions
The equation of a simple harmonic progressive wave along the negative direction of X-axis is
View SolutionConsider a standing wave formed on a string . It results due to the superposition of two waves travelling in opposite directions . The waves are travelling along the length of the string in the x - direction and displacements of elements on the string are along the y - direction . Individual equations of the two waves can be expressed as
Y1=6(cm)sin[5(rad/cm)x−4(rad/s)t]
Y2=6(cm)sin[5(rad/cm)x+4(rad/s)t] Here x and y are in cm.
Answer the following questions.
Amplitude of simple harmonic motion of a point on the string that is located at x=1.8cm will be
View Solution
Knowledge Check
Consider a standing wave formed on a string . It results due to the superposition of two waves travelling in opposite directions . The waves are travelling along the length of the string in the x - direction and displacements of elements on the string are along the y - direction . Individual equations of the two waves can be expressed as
Y1=6(cm)sin[5(rad/cm)x−4(rad/s)t]
Y2=6(cm)sin[5(rad/cm)x+4(rad/s)t] Here x and y are in cm.
Answer the following questions.
If one end of the string is at x=0 , positions of the nodes can be described asAx=nπ/5cm,wheren=0,1,2,…Bx=n2π/5cm,wheren=0,1,2,…Cx=nπ/5cm,wheren=0,1,3,5,…Dx=nπ/10cm,wheren=0,1,3,5,…Consider a standing wave formed on a string . It results due to the superposition of two waves travelling in opposite directions . The waves are travelling along the length of the string in the x - direction and displacements of elements on the string are along the y - direction . Individual equations of the two waves can be expressed as
Y1=6(cm)sin[5(rad/cm)x−4(rad/s)t]
Y2=6(cm)sin[5(rad/cm)x+4(rad/s)t] Here x and y are in cm.
Answer the following questions.
Maximum value of the y - positions coordinate in the simple harmonic motion of an element of the string that is located at an antinode will beA±6cmB±8cmC±12cmD±3cmThe displacement function of a wave travelling along positive x-direction is y=12+3x2att=0andbyy = (1)/(2) + 3(x - 2)^(2))att = 2 s,whereyandx are in metre. The velocity of the wave is
A2m/sB0.5m/sC1m/sD3m/s
A standing wave is formed by the superposition of two waves travelling in opposite directions. The transverse displacement is given by y(x,t)=0.5sin(5π4x)cos(200πt) What is the speed of the travelling wave moving in the position x direction?
View SolutionThe displacement function of a wave traveling along positive x-direction is y=12+2x2 at t=0and by y=12+2(x−2)2 at t=2s, where y and x are in metre. The velocity of the wave is:
View SolutionParticles on a string vibrate with amplitude of 6cm speed of wave is 300 m/s and angular frequency of oscillations is 245. Find wave equation of wave is travelling along positive x-direction.
View SolutionA standing wave is formed by the superposition of two waves travelling in the opposite directions. The transverse displacement is given by
y(x,t)=0.5sin(5π4x)cos(200πt)
What is the speed of the travelling wave moving in the postive X direction ?
View SolutionThe figure represent a longitudianl waave length travelling in positive x-direction . Then

View Solution

