The equation of a simple harmonic progressive wave along the negative direction of X-axis is
Consider a simple harmonic progressive wave travelling with a speed v along the positive x-axis. Let y denote the displacement of a particle of the medium from its mean position. At time t, the displacement of the particle of the medium situated at the origin is
y=Asinωt .....(1)
assuming that the epoch is zero. A is the amplitude of the wave and ω=2πn, where n is the frequency of the wave motion.
Consider a particle of the medium situated at point P at a distance x from the origin O as shown in the figure. This particle also performs SHM with the same amplitude A and the frequency n. Hoever, the disturbance at O reaches P only after some time. Hence, the particle at P lags behind the particle at O in phase. If α denotes the phase lag, the displacement of the particle at P is
y=Asin(ωt−α) ....(2)
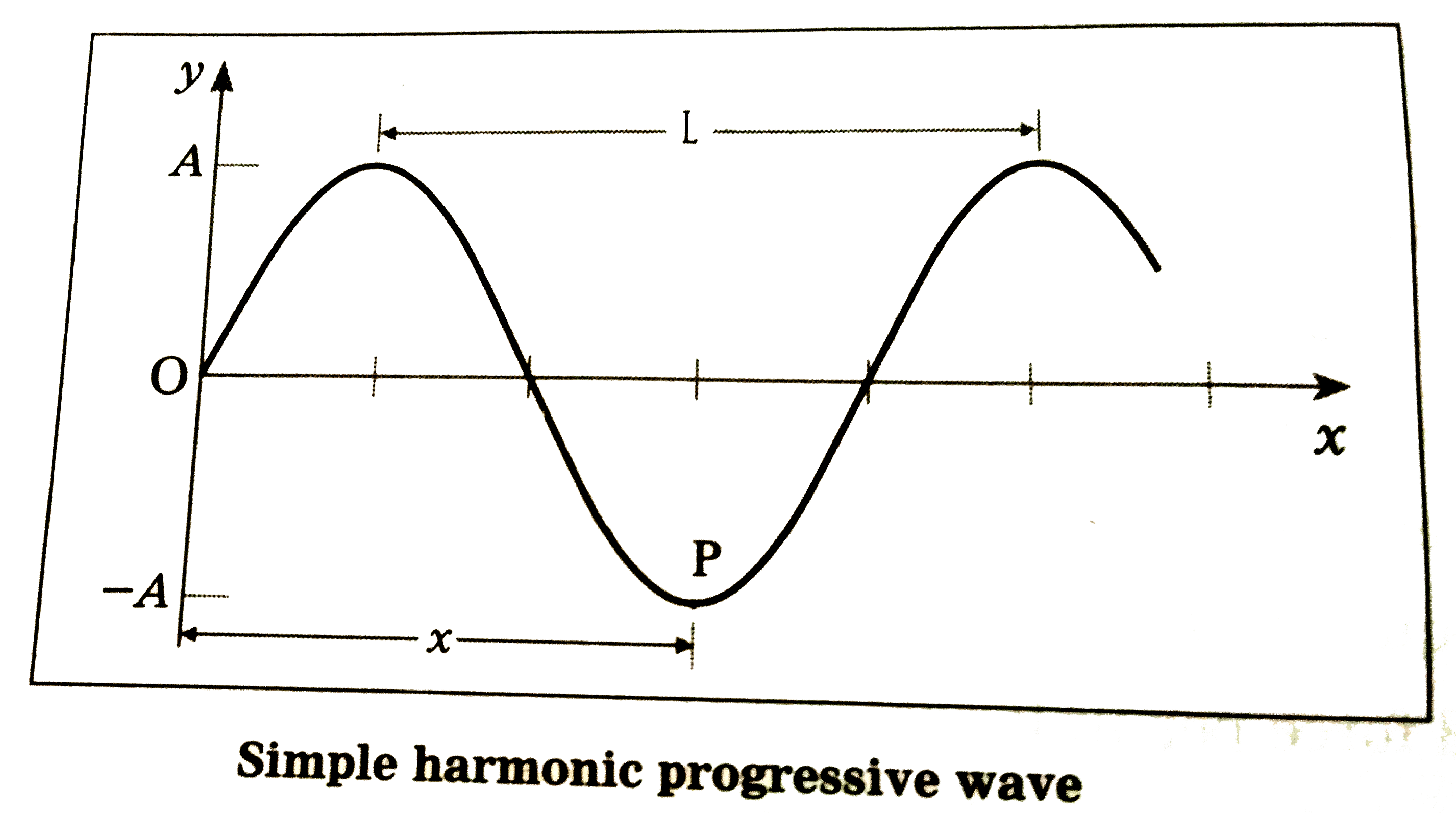
Since a path difference of one wavelength (λ) corresponds to a phase difference of 2π radians, a path difference of x corresponds to a phase difference of 2πλx radian. Thus, α=2πλx.
∴y=Asin(ωt−2πλx) ....(3)
If T is the period of vibrations, ω=2πT.
∴y=Asin(2πtT−2πλx)
∴y=Asin2π(tT−xλ) .....(4)
Equation (4) is the equation of a simple harmonic progressive wave travelling in the positive direction of the x-axis.
The frequency of vibrations, n=1T. Therefore, from Eq. (3),
y=Asin2π(nt−xλ) .....(5)
∴y=Asin2πn(t−xnλ)
But nλ=v, the speed of the wave.
∴y=Asin2πn(t−xv) ....(6)
Equations (5) and (6) are the other two different forms of the equation of a simple harmonic progressive wave.
[Note : Also, writing n=vλ in Eq. (6), we get,
y=Asin2πλ(vt−x) ....(7)
The quantity 2π/λ=k is called the propagation constant.
Substituting k=2π/λ in Eq. (1), we get,
y=Asin(ωt−kx) .....(8)
Equations (7) and (8) are two additional forms of the equation of a simple harmonic progressive wave.]
Topper's Solved these Questions
- DERIVATIONS-IBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - DERIVATIONS-IEXERCISE - Stationary Waves
5 Videos
- DERIVATIONS-IBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - DERIVATIONS-IEXERCISE - Kinetic Theory of Gases and Radiation
5 Videos
- DERIVATIONS-IBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - DERIVATIONS-IEXERCISE - Surface Tension
4 Videos
- DEFINITIONSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - DEFINITIONSEXERCISE - COMMUNICATION SYSTEMS
3 Videos
- DERIVATIONS-IIBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - DERIVATIONS-IIEXERCISE - Assignments
9 Videos
Similar Questions
Knowledge Check
The equation of a simple harmonic progressive wave along the positive direction of X axis is given by
Ay=asin2π[tT−xλ]By=asin(2πnt)Cy=asin2π[tT+xλ]Dy=acos(2πnt)The equation of a simple harmonic progressive wave having amplitude 5 mm, period 2 second and wavelength 2m and travelling along the positive direction of the x-axis is given by
Ay=5sin2π(t2−x2)By=5×10−3sin2π(2t−x2)Cy=5×10−3sin2π(t2−x2)Dy=5×10−3sinπ(2t−x)In the equation of a simple harmonic progressive wave of wavelength 'λ', the propagation constant is given by
A2π/λBπλCπ/λDλ/2π
Equation OF simple harmonic travelling wave
View SolutionDerive an expression for a one - dimensional simple harmonic progressive wave travelling in the direction of the positive x - axis. Express it in terms of A,λ, v , t and x .
View SolutionThe figure below is a representation of a simple harmonic progressive in the negative X-axis, at a given instant. The direction of the velocity of the particle at stage P in the figure is best represent by the arrow.
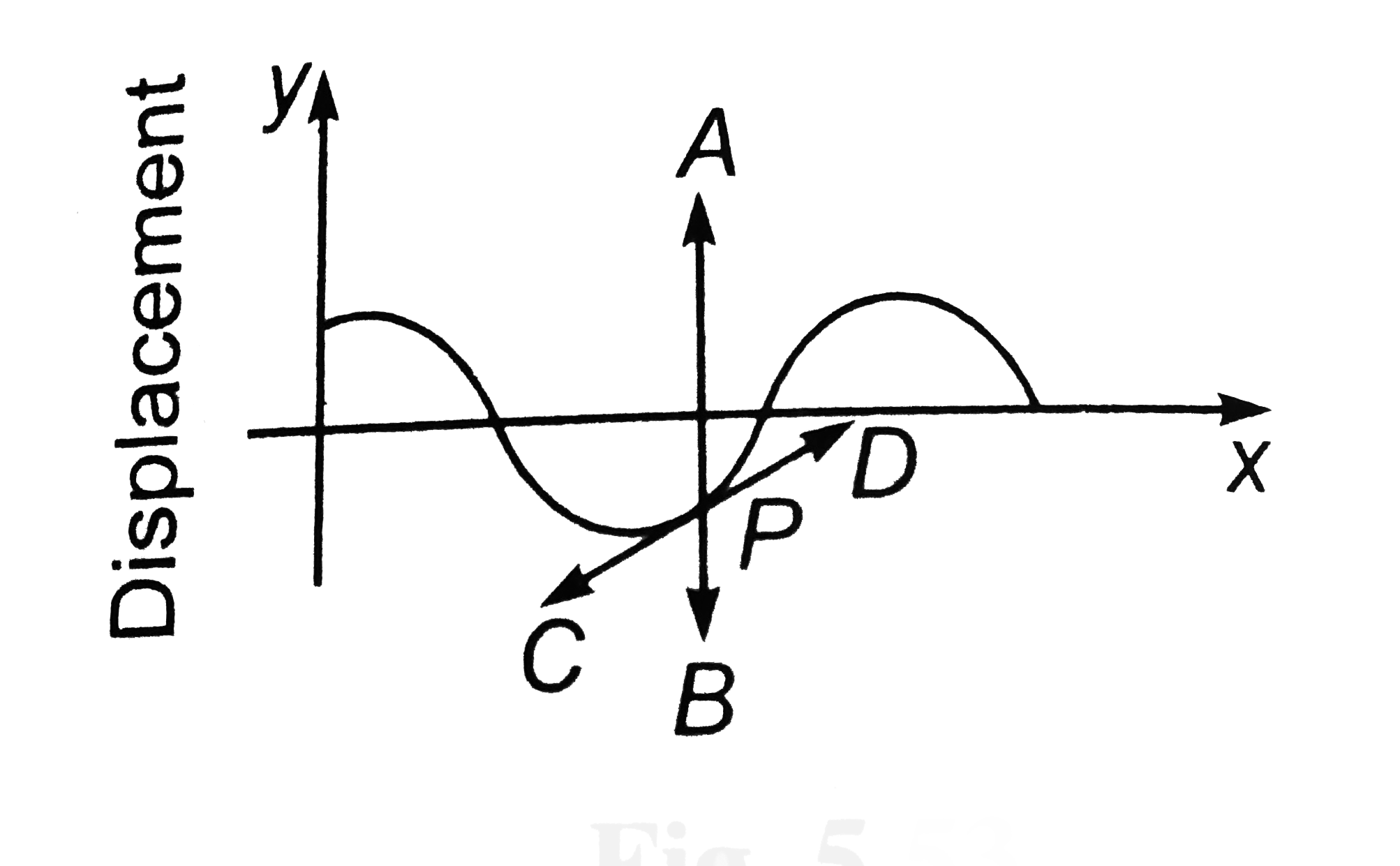
View SolutionThe equation of a simple harmonic progressive wave is given by y=12sin(ωt−4x)m. What is the distance between 2 particles on the wave, having a phase difference of π/2 ?
View SolutionThe equation of progressive wave travelling a long positive direction of x axis having a amplitude of 0.04 m, frequency 440 Hz and wave velocity 330 m/s, is
View Solution
