man of height h walks in a straight path towards a lamp post of height H with uniform velocity u. Then the velocity of the edge of the shadow on the ground will be :-
Hu(H−h)
Hu(H+h)
(H−h)Hu
(H+h)Hu
The correct Answer is:A
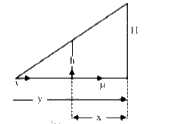
V=dydt= velocity of the edge of the shadow on the ground
μ=dxdt= speed of man.
Hy=hy−x
Hy−Hx=hy
y(H−h)=Hx
differentiating 60th side
dydt(H−h)=Hdxdt
⇒V=HμH−h
Topper's Solved these Questions
Similar Questions
A vertical lamp-post of height h stands at a point on the boundary of a circular field. A man of height a is running round the boundary. Prove that the end of the shadow of the man will also travel on a circle. Find the ratio of the radii of the two circles.
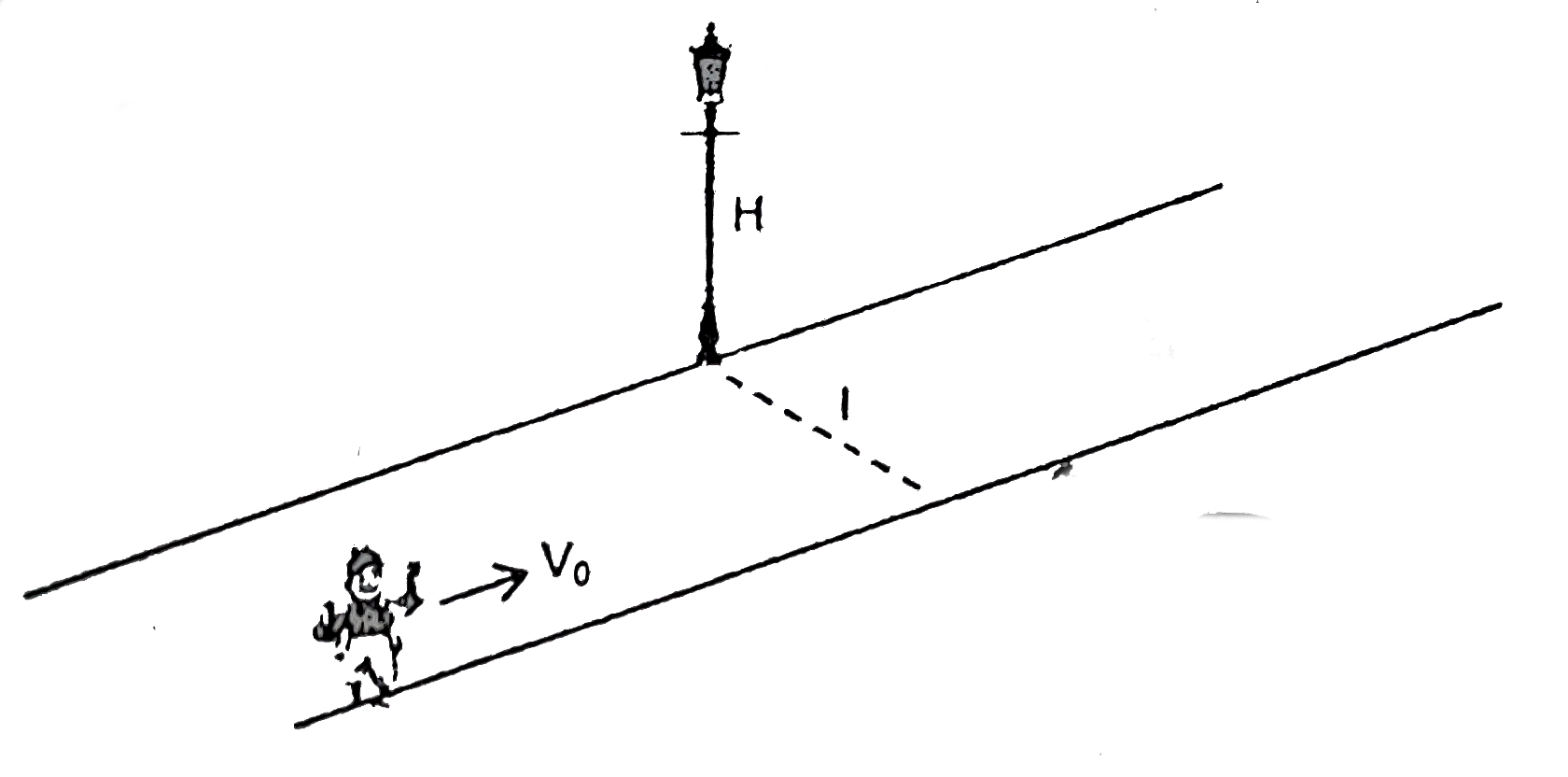
View SolutionA man of height h is walking at constant speed v0 along edge of a straight horizontal road. There is a lamp post of height H=2h on the other edge as shown. If speed of tip of shadow of his head is nv0 then find n.
View Solution
Knowledge Check
A man of height 2m walks directly away from a lamp of height 5 m on a level road at 3m/s. The rate at which the length of his shadow is increasing is
A1m/sB2m/sC3m/sD4m/sA man of 2 m height walks at a uniform speed to 6 km/h, away from a lamp post of 6 m height. The rate at which the length of his shadow increase is
A2 km/hB1 km/hC3 km/hD6 km/hA man of 2m height walks at a uniform speed of 6kmh−1 away from a lamp post of 6m height. The rate at which the length of his shadow increase in
A2kmh−1B1kmh−1C3kmh−1D6kmh−1
A man of height 1.7 m walks at a uniform speed of 6.6 m/min from a lamp post which is 5m high.Find the rate at which the length of his shadow increases.
View SolutionA man is walking due west with a velocity 3km/h and rain appears to be falling vertically with a velocity 4km/h. Find the velocity of rain with respect to the ground.
View SolutionA man 2 metres tall walks away from a lamp post 5 metres height at the rate of 4.8 km/hr. The rate of increase of the length of his shadow, is
View SolutionA man of height 'h' is walking away from a street lamp with a constant speed 'v'. The height of the street lamp is 3h. The rate at which the length of the man's shadow is increasing when he is at a distance 10 h from the base of the street lamp is
View SolutionA man of height 'h'is walking away from a street lamp with a constant speed'v'.The height of the street lamp is 3hThe rate at which of the length of man's shadow is increasingwhen he is at a distance 10hfrom the base of the street lamp is:
View Solution

