The string of a simple pendulum replaced by a uniform rod of length $L$ and mass $M$ while the bob has a mass $m$ . It is allowed to make small oscillation. Its time period is

A

$2 π \sqrt{(\frac{2 M}{3 m}) \frac{L}{g}}$

B

$2 π \sqrt{\frac{2 (M + 3 m) L}{3 (M + 2 m) g}}$

C

$2 π \sqrt{(\frac{M + m}{M + 3 m}) \frac{L}{g}}$

D

$2 π \sqrt{(\frac{2 m + M}{3 (M + 2 m)}) \frac{L}{g}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

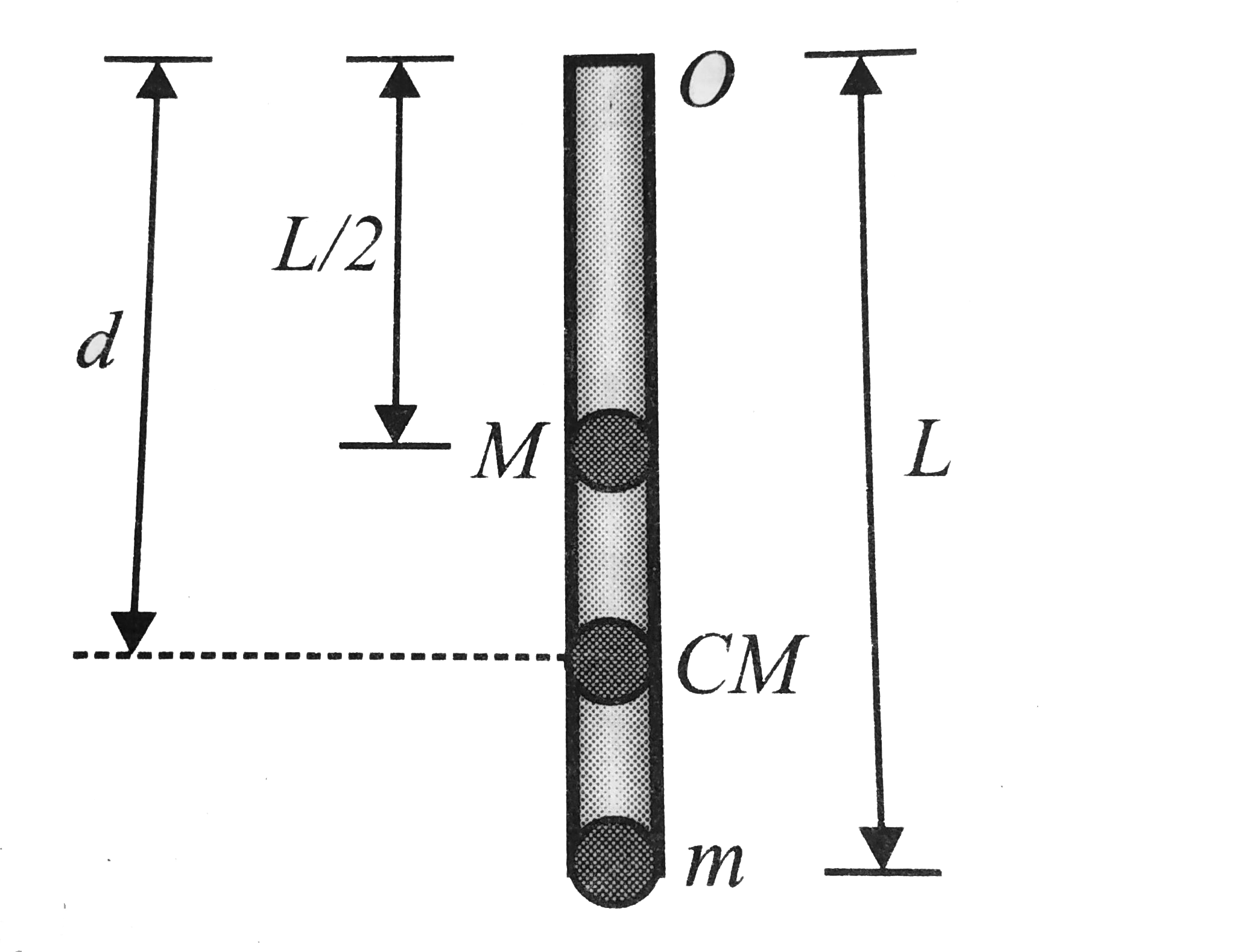
When the rod is replaced by the string the simple pendulum will act as compound pendulum for which time period is given by
$T = 2 π \sqrt{\frac{I_{0}}{M g d}}$ ..(i)
$I_{0} =$ moment of inertia about of suspension
$= \frac{M L^{2}}{3} + m L^{2} = \frac{(M + 3 m) L^{2}}{3}$
$M' =$ total mass $= (M + m)$
$d =$ separation between point of suspension and centre of mass of the pendulum
$= \frac{M (\frac{L}{2}) + m (L)}{(M + m)} = \frac{(M + 2 m) L}{2 (M + m)}$
Substituting the values in Eq. (i) we get
$\Rightarrow T = 2 π \sqrt{\frac{2 (M + 3 m) L}{3 (M + 2 m) g}}$

|

Updated on:21/07/2023

Class 11 PHYSICS SIMPLE HARMONIC MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
If the metal bob of a simple pendulum is replaced by a wooden bob, then its time period will
AIncrease
BDecrease
CRemain the same
DFirst increase then decrease
Question 2 - Select One
There is a rod of length $l$ and mass $m$ . It is hinged at one end to the ceiling. The period of small oscillation is
A $T = 2 π \sqrt{\frac{2 l}{3 g}}$
B $T = π \sqrt{\frac{l}{3 g}}$
C $T = 2 π \sqrt{\frac{l}{3 g}}$
D $T = 2 π \sqrt{\frac{l}{g}}$
Question 3 - Select One
A simple pendulum has time period T. A uniform rod, whose length is the same as that of the pendulum, undergoes small oscillations about its upper end. Its time period of oscillation will be -
A $< T$
BT
C $> T$
Dmay be (A), (B) or (C) depending on whether T is $<$ equal to or $> 2$ seconds

CENGAGE PHYSICS-LINEAR AND ANGULAR SIMPLE HARMONIC MOTION-Single Correct

Home
Ask Doubt
Profile