Two straight infinitely long and thin parallel wires are spaced 0.1m apart and carry a current of 10A each. Find the magnetic field at a point distance 0.1m from both wires in the two cases when the currents are in the (a) same and (b) opposite directions.
To solve the problem of finding the magnetic field at a point equidistant from two parallel wires carrying currents in both the same and opposite directions, we will follow these steps:
Given:
- Distance between the wires, d=0.1m
- Current in each wire, I=10A
- Distance from each wire to the point of interest, r=0.1m
Step 1: Calculate the magnetic field due to one wire
The magnetic field B at a distance r from a long straight wire carrying current I is given by the formula:
B=μ0I2πr
where μ0=4π×10−7T m/A.
Substituting the values:
B=(4π×10−7)×102π×0.1
B=4×10−60.2=2×10−5T
Step 2: Analyze the case when currents are in the same direction (Case a)
When the currents are in the same direction, the magnetic fields produced by both wires at the point of interest will add up.
- The direction of the magnetic field due to each wire can be determined using the right-hand rule. For both wires carrying current upwards, the magnetic field at the point will be directed out of the page (towards the observer).
Thus, the total magnetic field Btotal at the point is:
Btotal=B1+B2=2×10−5+2×10−5=4×10−5T
Step 3: Analyze the case when currents are in opposite directions (Case b)
When the currents are in opposite directions, the magnetic fields produced by both wires at the point of interest will oppose each other.
- For the wire with current flowing upwards, the magnetic field at the point will be directed out of the page.
- For the wire with current flowing downwards, the magnetic field at the point will be directed into the page.
Thus, the total magnetic field Btotal at the point is:
Btotal=B1−B2=2×10−5−2×10−5=0T
Final Results:
- (a) When the currents are in the same direction, the magnetic field at the point is 4×10−5T out of the page.
- (b) When the currents are in opposite directions, the magnetic field at the point is 0T.
- Distance between the wires, d=0.1m
- Current in each wire, I=10A
- Distance from each wire to the point of interest, r=0.1m
The magnetic field B at a distance r from a long straight wire carrying current I is given by the formula:
B=μ0I2πr
where μ0=4π×10−7T m/A.
B=(4π×10−7)×102π×0.1
B=4×10−60.2=2×10−5T
When the currents are in the same direction, the magnetic fields produced by both wires at the point of interest will add up.
Btotal=B1+B2=2×10−5+2×10−5=4×10−5T
When the currents are in opposite directions, the magnetic fields produced by both wires at the point of interest will oppose each other.
- For the wire with current flowing downwards, the magnetic field at the point will be directed into the page.
Btotal=B1−B2=2×10−5−2×10−5=0T
- (a) When the currents are in the same direction, the magnetic field at the point is 4×10−5T out of the page.
- (b) When the currents are in opposite directions, the magnetic field at the point is 0T.
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Solved Example
20 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Concept Exercise 2.1
35 Videos
- SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - CENGAGE PHYSICSCHAPTER - SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - QUESTION BANK
12 Videos
- THERMAL PROPERTIES OF MATTERBOOK - CENGAGE PHYSICSCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Question Bank
40 Videos
Similar Questions
Two long parallel wires are carrying currents as shown
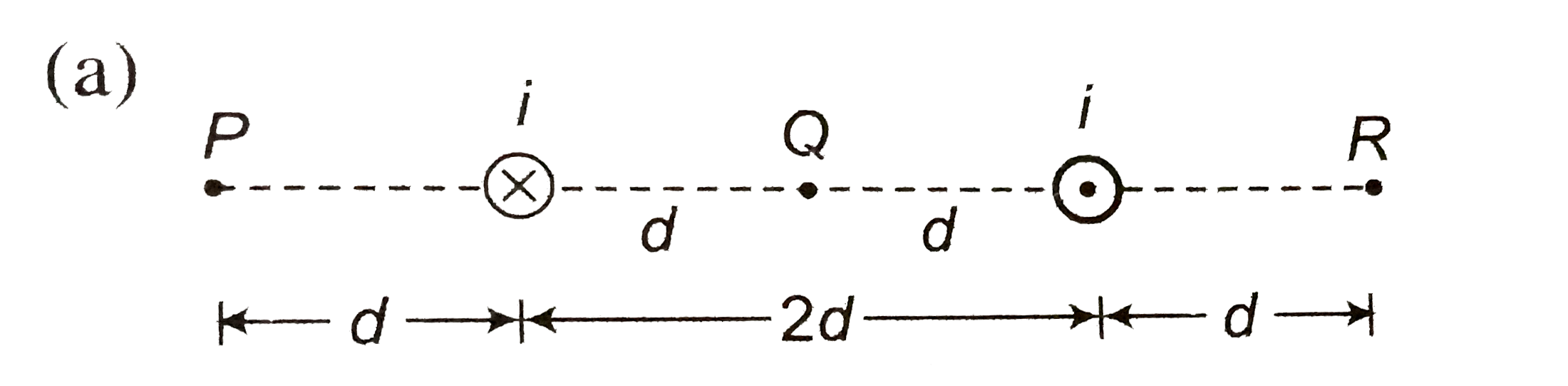
Find magnitude and direction of magnetic field at P,Q and R.
(b) (i)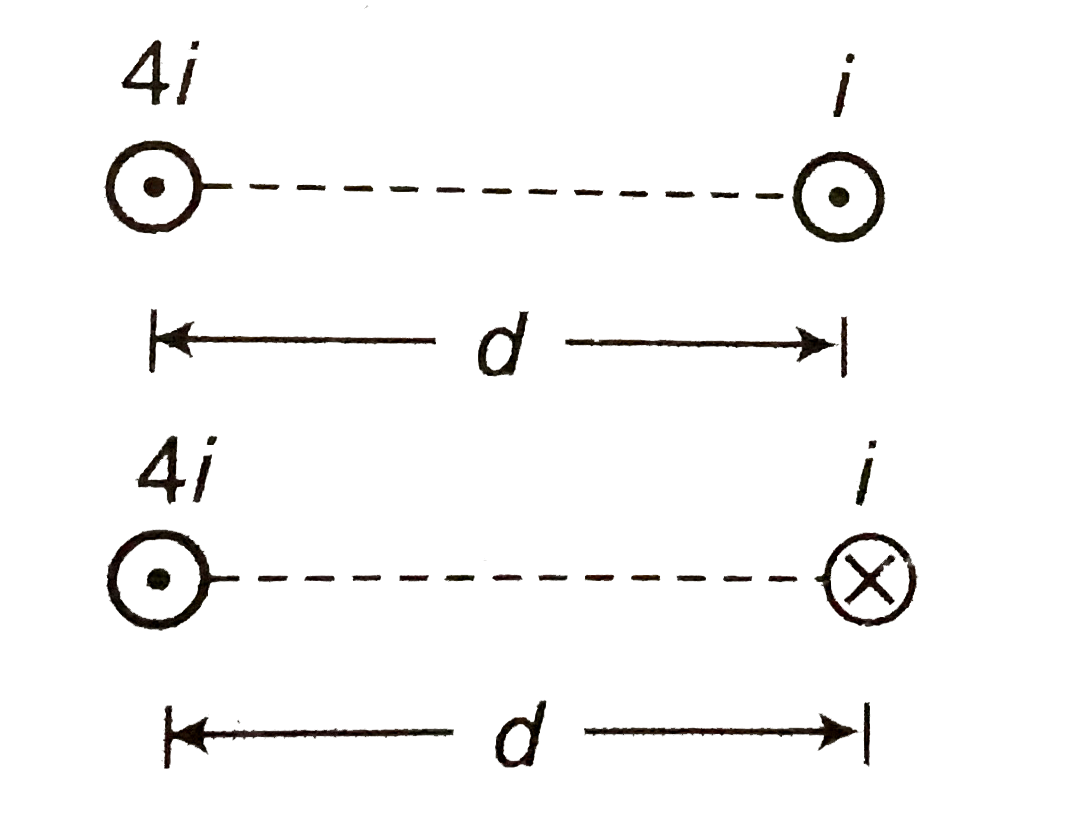
(ii)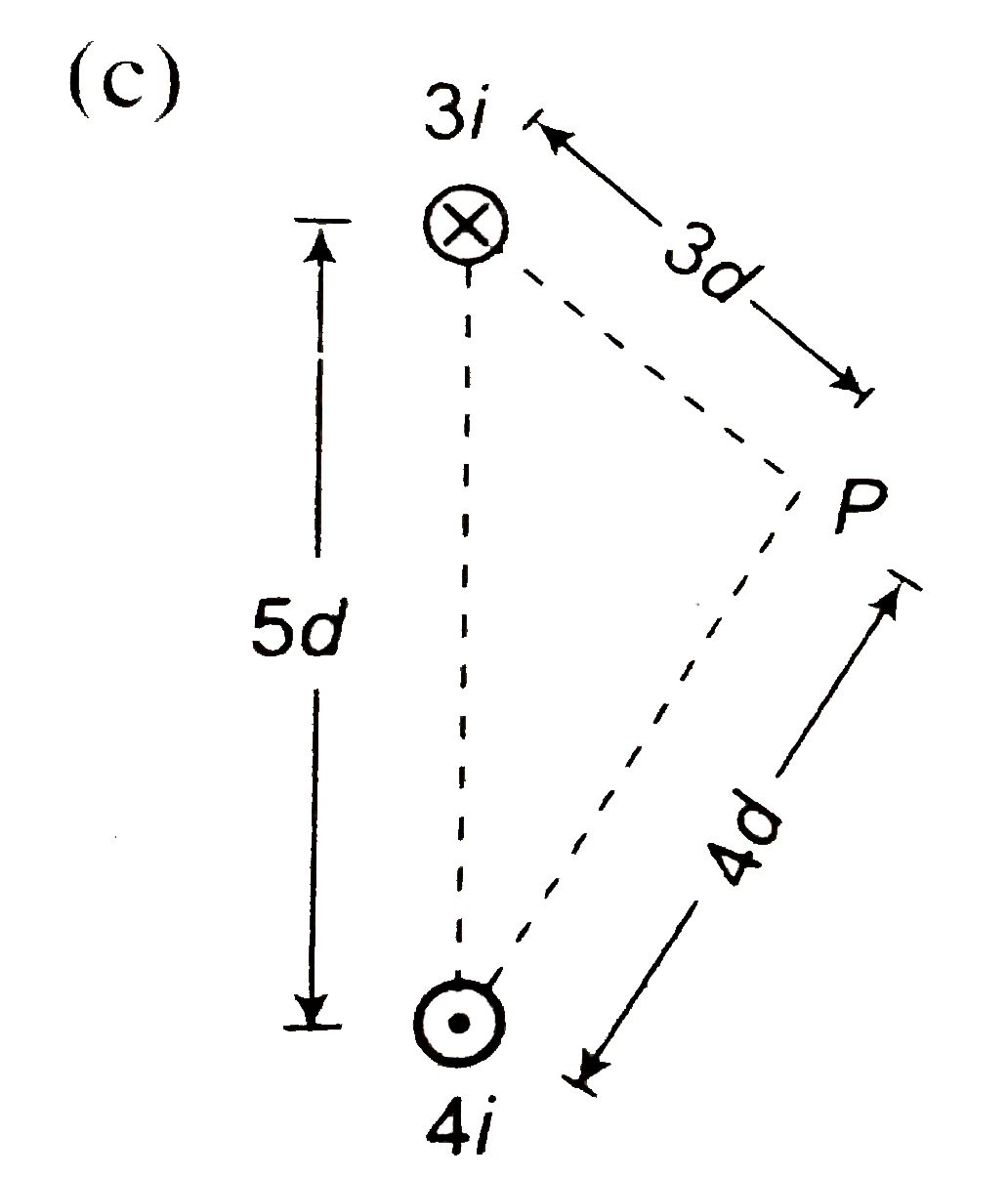
At what distance from left wire, magnetic field is zero on the line joining the wires.
Find magnitude of magnetic field at P.
(d) Two straight infinitely long and thin parallel wires are spaced d distance apart and carry a current i each. find the magnetic field at a point distance d from both wires when the currents are in the (i) same and (ii) opposite directions.
View SolutionTwo long parallel transmission lines 40.0cm apart carry 25.0A and 75.0Acurrents. Find an locations where the net magnetic field of the two wires is zero if these currents are in
(a) the same direction (b) the opposite direction
View Solution
Knowledge Check
Two infinitely long parallel wires carry equal current in same direction. The magnetic field at a mid point in between the two wires is
ATwice the magnetic field produced due to each of the wiresBHalf of the magnetic field produced due to each of the wiresCSquare of the magnetic field produced due to each of the wiresDZeroTwo infinitely long parallel wires carry equal currents in the same direction .The magnetic field at a mind point in between the two wires is
ASquare of the magnetic field produced due to each of the wiresBhalf of the magnetic field produced due to each of the wiresCtwice the magnetic field produced due to each of the wiresDzeroTwo thin, long, parallel wires, separated by a distance 'd' carry a current of 'i' A in the same direction. They will
Arepel each other with a force of μ0i2/(2πd)Battract each other with a force of μ0i2/(2πd)Crepel each other with a force of μ0i2/(2πd2)Dattract each other with a force of μ0i2/(2πd2)
Two long parallel wires are placed at a distance of 12cm from each other in air. Each wire has a current of 3A. Calculate the magnetic field at a point mid way between them when the currents in them are : (i) in the same direction and (ii) in opposite direction.
View SolutionTwo parallel wires in free spaces are 10cm apart and each carries a current of 10A in the same direction. The force one wire exerts on the other per metre of length is
View SolutionTwo long parallel wires placed 0.08 m apart, carry currents 3 A and 5 A in the same direction. what is the distance from the conductor carrying the larger current to the point where the resultant magnetic field is zero?
View SolutionTwo long parallel wires are separated by a distance of 2m. They carry a current of 1A each in opposite direction. The magnetic induction at the midpoint of a straight line connecting these two wires is
View SolutionThe direction of magnetic field at a point due to an infinitely long wire carrying current is
View Solution
