Two long parallel transmission lines 40.0cm apart carry 25.0A and 75.0Acurrents. Find an locations where the net magnetic field of the two wires is zero if these currents are in
(a) the same direction (b) the opposite direction
The correct Answer is:A
To solve the problem of finding locations where the net magnetic field of two long parallel transmission lines is zero, we will analyze two scenarios: (a) when the currents are in the same direction and (b) when the currents are in opposite directions.
Given Data:
- Distance between the wires, d=40.0cm=0.4m
- Current in wire A, I1=25.0A
- Current in wire B, I2=75.0A
(a) Currents in the Same Direction
1. Understanding Magnetic Fields:
- The magnetic field B due to a long straight current-carrying wire at a distance r is given by:
B=μ0I2πr
- For two wires carrying currents in the same direction, the magnetic fields will add up between the wires and cancel out outside.
2. Setting Up the Equation:
- Let x be the distance from wire A where the magnetic field is zero.
- The distance from wire B will then be 0.4−x.
- The magnetic field due to wire A at distance x:
BA=μ0I12πx
- The magnetic field due to wire B at distance 0.4−x:
BB=μ0I22π(0.4−x)
- Since both fields are in the same direction, we set them equal to each other:
I1x=I20.4−x
3. Substituting Values:
25x=750.4−x
4. Cross-multiplying:
25(0.4−x)=75x
10−25x=75x
10=100x
x=0.1m=10cm
(b) Currents in Opposite Directions
1. Understanding Magnetic Fields:
- When the currents are in opposite directions, the magnetic fields will oppose each other in the region between the wires.
2. Setting Up the Equation:
- Let x be the distance from wire A where the magnetic field is zero.
- The distance from wire B will be 0.4+x (since we are considering points outside the wires).
- The magnetic field due to wire A at distance x:
BA=μ0I12πx
- The magnetic field due to wire B at distance 0.4+x:
BB=μ0I22π(0.4+x)
- Set the magnitudes equal since they are in opposite directions:
I1x=I20.4+x
3. Substituting Values:
25x=750.4+x
4. Cross-multiplying:
25(0.4+x)=75x
10+25x=75x
10=50x
x=0.2m=20cm
Summary of Results:
- (a) The location where the magnetic field is zero when currents are in the same direction is 10 cm from wire A.
- (b) The locations where the magnetic field is zero when currents are in opposite directions is 20 cm from wire A.
- Distance between the wires, d=40.0cm=0.4m
- Current in wire A, I1=25.0A
- Current in wire B, I2=75.0A
- The magnetic field B due to a long straight current-carrying wire at a distance r is given by:
B=μ0I2πr
- For two wires carrying currents in the same direction, the magnetic fields will add up between the wires and cancel out outside.
- Let x be the distance from wire A where the magnetic field is zero.
- The distance from wire B will then be 0.4−x.
- The magnetic field due to wire A at distance x:
BA=μ0I12πx
- The magnetic field due to wire B at distance 0.4−x:
BB=μ0I22π(0.4−x)
- Since both fields are in the same direction, we set them equal to each other:
I1x=I20.4−x
25x=750.4−x
25(0.4−x)=75x
10−25x=75x
10=100x
x=0.1m=10cm
- When the currents are in opposite directions, the magnetic fields will oppose each other in the region between the wires.
- Let x be the distance from wire A where the magnetic field is zero.
- The distance from wire B will be 0.4+x (since we are considering points outside the wires).
- The magnetic field due to wire A at distance x:
BA=μ0I12πx
- The magnetic field due to wire B at distance 0.4+x:
BB=μ0I22π(0.4+x)
- Set the magnitudes equal since they are in opposite directions:
I1x=I20.4+x
25x=750.4+x
25(0.4+x)=75x
10+25x=75x
10=50x
x=0.2m=20cm
- (a) The location where the magnetic field is zero when currents are in the same direction is 10 cm from wire A.
- (b) The locations where the magnetic field is zero when currents are in opposite directions is 20 cm from wire A.
Topper's Solved these Questions
- MAGNETICSBook:DC PANDEYChapter:MAGNETICSExercise:INTRODUCTORY EXERCISE
Explore 1 Video
- MAGNETICSBook:DC PANDEYChapter:MAGNETICSExercise:SUBJECTIVE_TYPE
Explore 1 Video
- MAGNETICSBook:DC PANDEYChapter:MAGNETICSExercise:MCQ_TYPE
Explore 1 Video
- MAGNETIC FIELD AND FORCESBook:DC PANDEYChapter:MAGNETIC FIELD AND FORCESExercise:Medical entrance s gallery
Explore 59 Videos
- MAGNETISM AND MATTERBook:DC PANDEYChapter:MAGNETISM AND MATTERExercise:Medical gallery
Explore 1 Video
Similar Questions
Two straight infinitely long and thin parallel wires are spaced 0.1m apart and carry a current of 10A each. Find the magnetic field at a point distance 0.1m from both wires in the two cases when the currents are in the (a) same and (b) opposite directions.
View SolutionTwo long parallel wires are carrying currents as shown
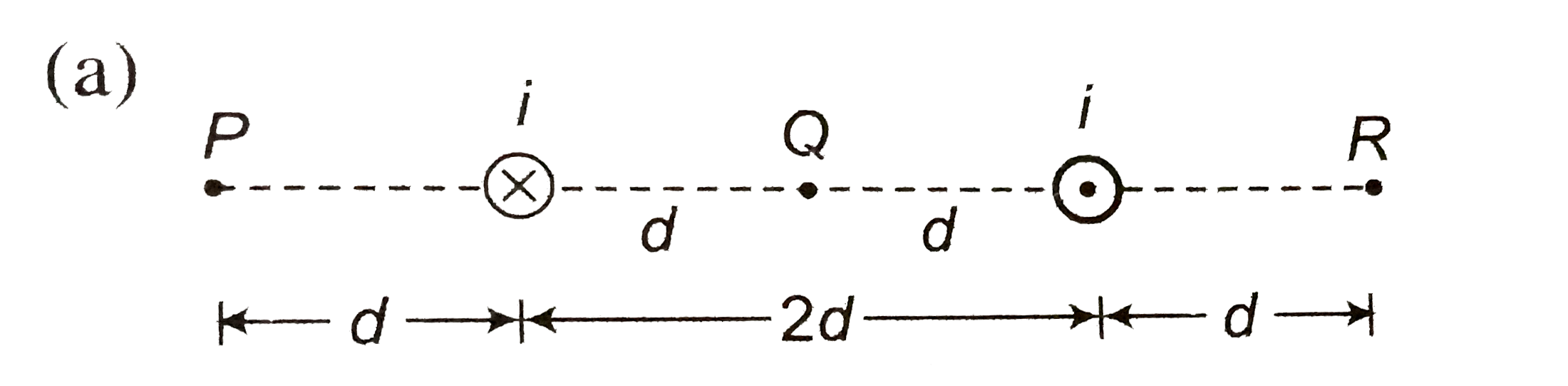
Find magnitude and direction of magnetic field at P,Q and R.
(b) (i)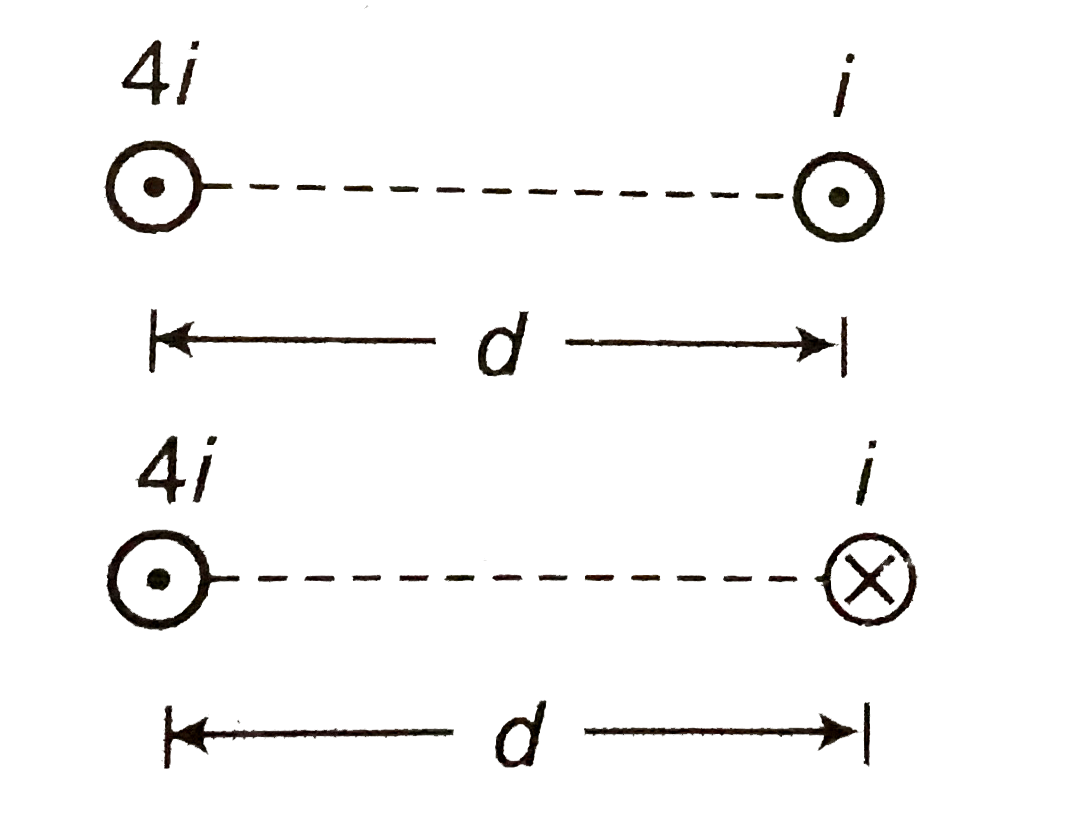
(ii)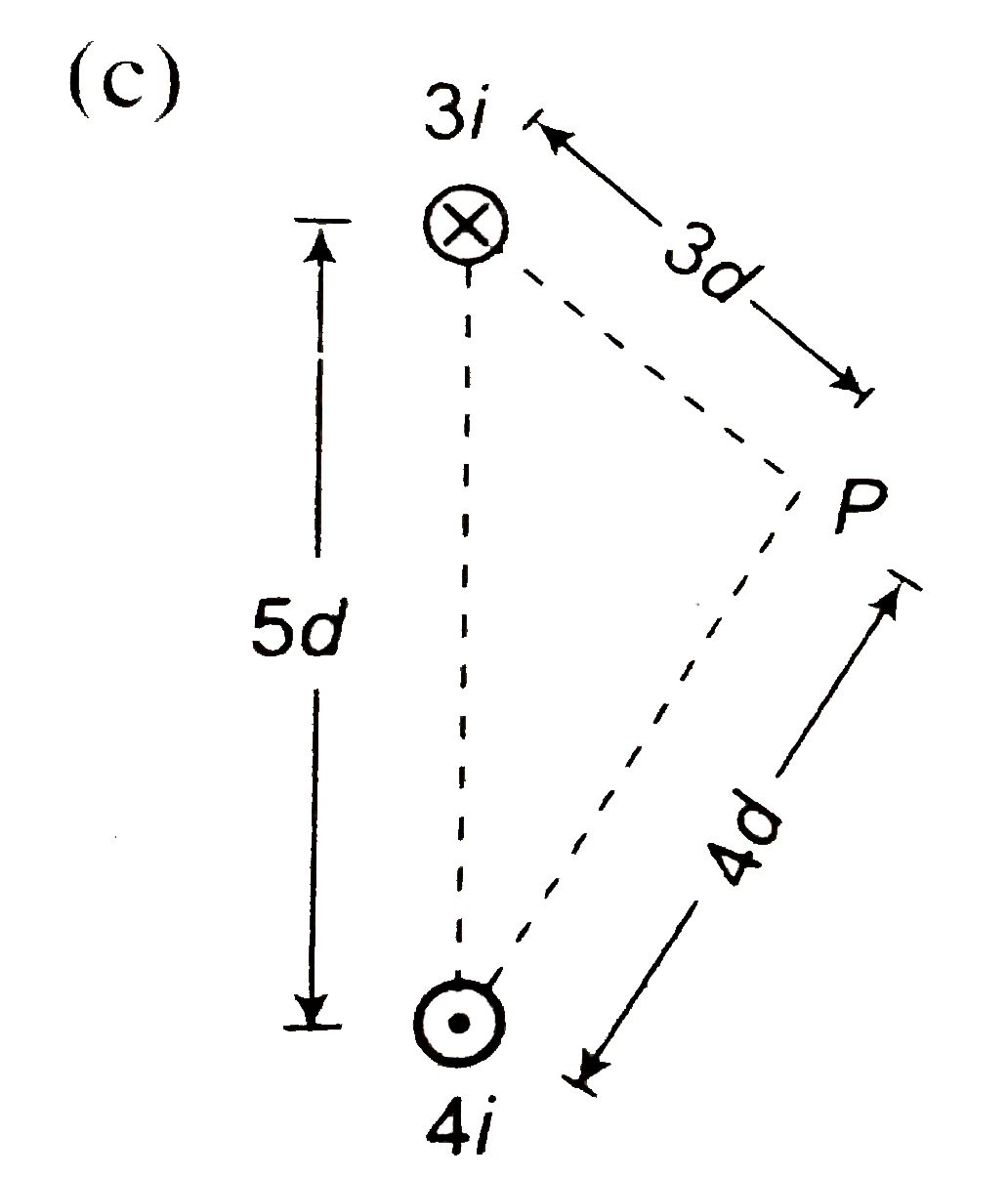
At what distance from left wire, magnetic field is zero on the line joining the wires.
Find magnitude of magnetic field at P.
(d) Two straight infinitely long and thin parallel wires are spaced d distance apart and carry a current i each. find the magnetic field at a point distance d from both wires when the currents are in the (i) same and (ii) opposite directions.
View Solution
Knowledge Check
Two very long, straight wires carrying, currents as shown in Fig. Find all locations where the net magnetic field is zero.
 Ay=√2xBy=xCy=−xDy=−(x2)
Ay=√2xBy=xCy=−xDy=−(x2)Two long parallel wires are 30 cm apart carrying currents 10 A and 15 A respectively in the same direction. The force acting over a length of 5 m of the wires is
A5×10−4N, (attraction)B1×10−4N, (attraction)C5×10−4N, (repulsion)D1×10−4N, (repulsion)Two free parallel wires carrying currents in opposite direction
AAttract each otherBRepel each otherCNeither attract nor repelDGet rotated to be perpendicular to each other
Two long parallel wires are placed at a distance of 12cm from each other in air. Each wire has a current of 3A. Calculate the magnetic field at a point mid way between them when the currents in them are : (i) in the same direction and (ii) in opposite direction.
View SolutionFigure shows two long parallel straight wires distance 5cm apart carrying currents 4A and 10A in opposite directions. Find the position of a point where the resultant magnetic field due to current in two wires in zero.
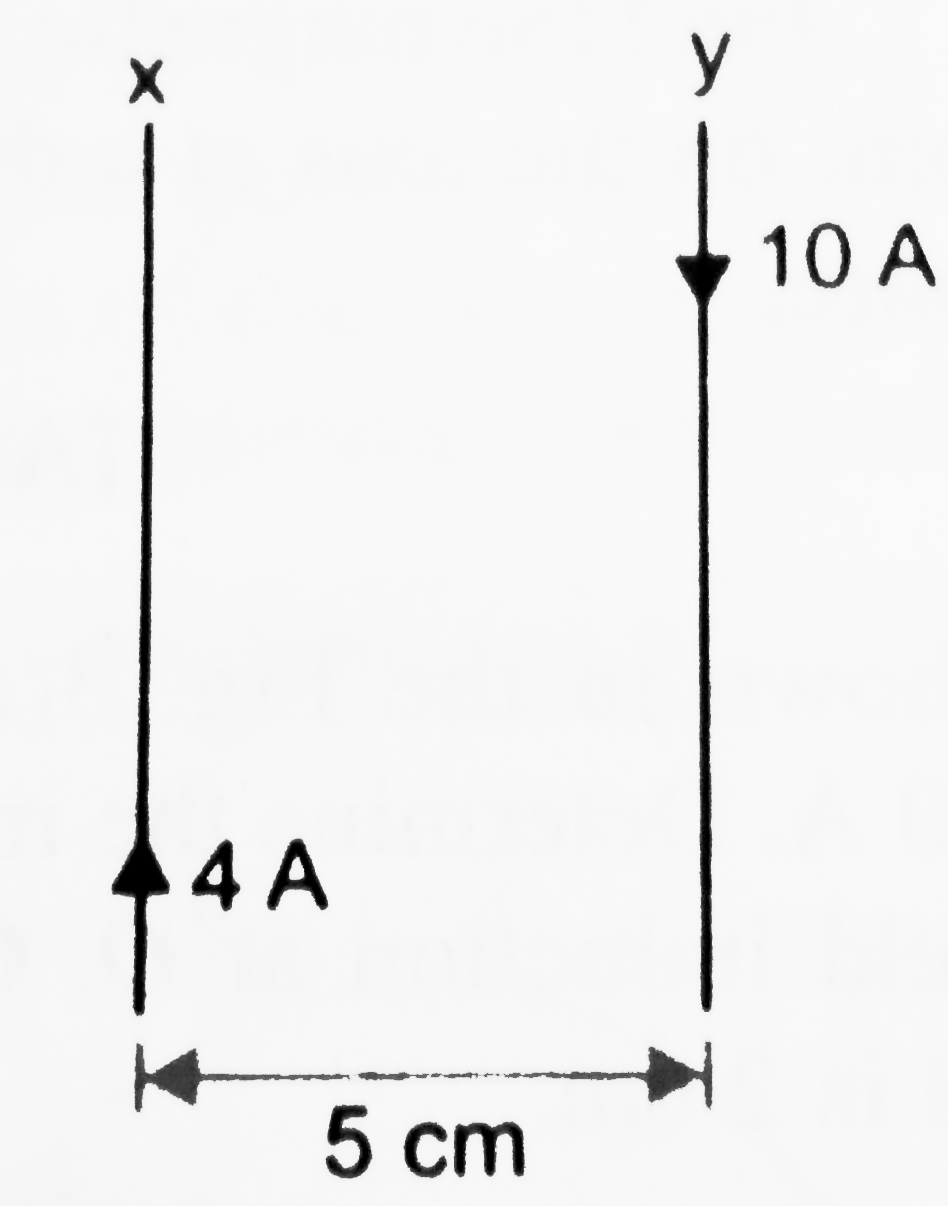
View SolutionTwo long parallel wires placed 0.08 m apart, carry currents 3 A and 5 A in the same direction. what is the distance from the conductor carrying the larger current to the point where the resultant magnetic field is zero?
View SolutionTwo free parallel wires carrying currents in opposite directions
View SolutionTwo free parallel wires carrying currents in opposite directions
View Solution

