Two long parallel wires are placed at a distance of 12cm from each other in air. Each wire has a current of 3A. Calculate the magnetic field at a point mid way between them when the currents in them are : (i) in the same direction and (ii) in opposite direction.
The correct Answer is:(i) Zero (ii) 2×10−5T, normally outwards
To solve the problem of calculating the magnetic field at a point midway between two long parallel wires carrying currents, we will follow these steps:
Given Data:
- Distance between the wires, d=12cm=0.12m
- Current in each wire, I=3A
Step 1: Calculate the distance from each wire to the midpoint
Since the wires are parallel and the point of interest is midway between them, the distance from each wire to the midpoint is:
D=d2=0.122=0.06m
Step 2: Calculate the magnetic field due to one wire
The magnetic field B due to a long straight wire at a distance D is given by the formula:
B=μ0I2πD
where μ0 (the permeability of free space) is approximately 4π×10−7T m/A.
Substituting the values:
B=(4π×10−7)×32π×0.06
B=(4×3×10−7)2×0.06
B=12×10−70.12=10−6T=1μT
Step 3: Case (i) - Currents in the same direction
When the currents are in the same direction, the magnetic fields due to both wires at the midpoint will be in the same direction (let's say into the page).
Thus, the total magnetic field Btotal at the midpoint is:
Btotal=B1+B2=1μT+1μT=2μT
Step 4: Case (ii) - Currents in opposite directions
When the currents are in opposite directions, the magnetic fields due to the wires at the midpoint will be in opposite directions.
Thus, the total magnetic field Btotal at the midpoint is:
Btotal=B1−B2=1μT−1μT=0T
Final Answers:
(i) When currents are in the same direction:
Btotal=2μT
(ii) When currents are in opposite directions:
Btotal=0T
- Distance between the wires, d=12cm=0.12m
- Current in each wire, I=3A
Since the wires are parallel and the point of interest is midway between them, the distance from each wire to the midpoint is:
D=d2=0.122=0.06m
The magnetic field B due to a long straight wire at a distance D is given by the formula:
B=μ0I2πD
where μ0 (the permeability of free space) is approximately 4π×10−7T m/A.
B=(4π×10−7)×32π×0.06
B=(4×3×10−7)2×0.06
B=12×10−70.12=10−6T=1μT
When the currents are in the same direction, the magnetic fields due to both wires at the midpoint will be in the same direction (let's say into the page).
Btotal=B1+B2=1μT+1μT=2μT
When the currents are in opposite directions, the magnetic fields due to the wires at the midpoint will be in opposite directions.
Btotal=B1−B2=1μT−1μT=0T
(i) When currents are in the same direction:
Btotal=2μT
Btotal=0T
Topper's Solved these Questions
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBook:PRADEEPChapter:MAGNETIC EFFECT OF CURRENT AND MAGNETISMExercise:Test Your Grip (a)
Explore 1 Video
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBook:PRADEEPChapter:MAGNETIC EFFECT OF CURRENT AND MAGNETISMExercise:Test Your Grip (c)
Explore 1 Video
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBook:PRADEEPChapter:MAGNETIC EFFECT OF CURRENT AND MAGNETISMExercise:Value Based Questions
Explore 2 Videos
- ELECTROSTATICSBook:PRADEEPChapter:ELECTROSTATICSExercise:ASSERTION-REASON TYPE QUESTIONS
Explore 2 Videos
- OPTICSBook:PRADEEPChapter:OPTICSExercise:Multiple choice questions
Explore 1 Video
Similar Questions
(a) Derive the expression for the force acting per unit length between two long straight parallel current carrying conductors. Hence, define one ampere.
(b) Two long parallel straight conductors are placed 12 cm apart in air. They carry equal currents of 3 A each. Find the magnitude and direction of the magnetic field at a point midway between them (drawing a figure) when the currents in them flow in opposite directions.
View SolutionTwo long parallel wires are carrying currents as shown
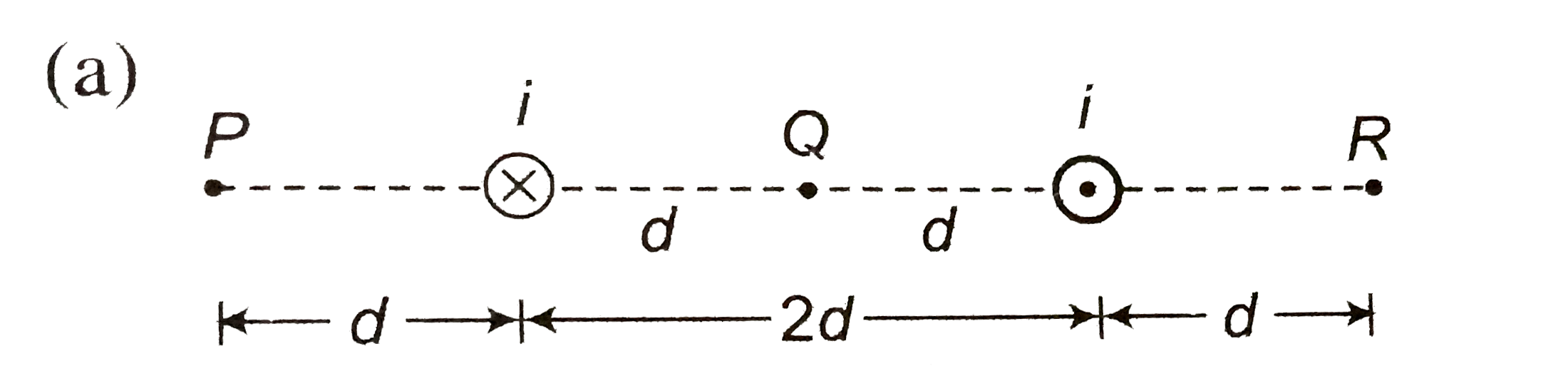
Find magnitude and direction of magnetic field at P,Q and R.
(b) (i)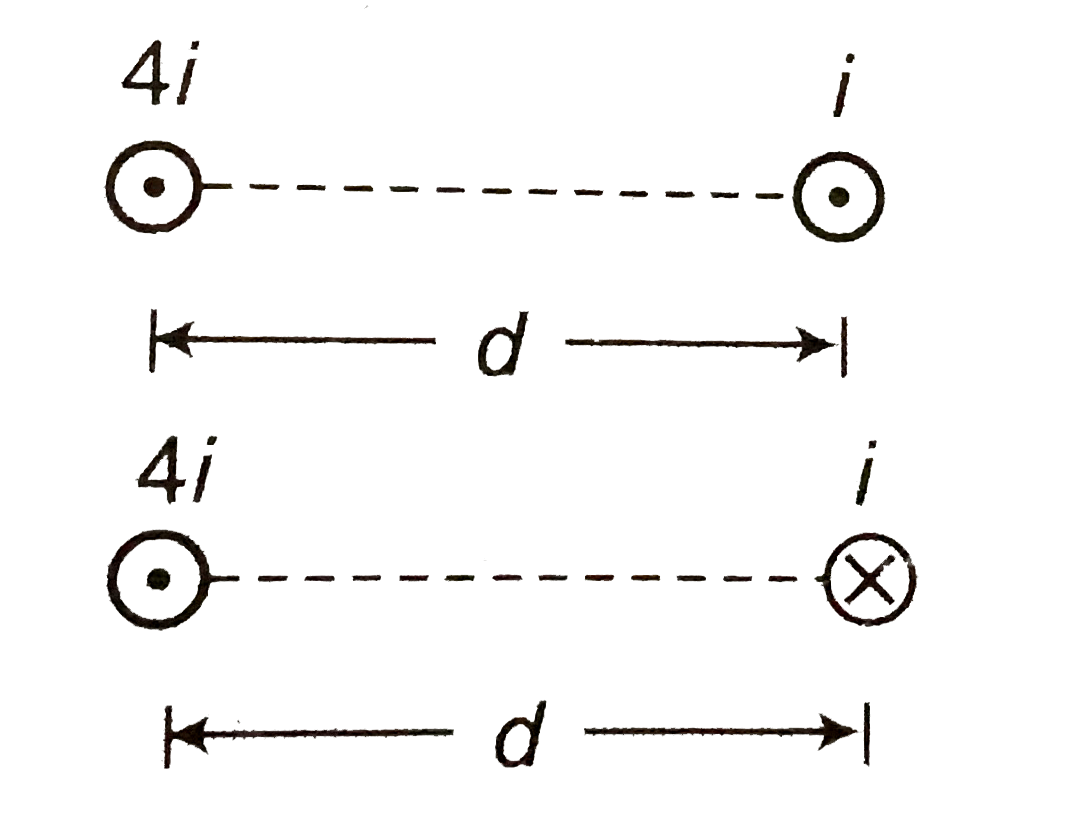
(ii)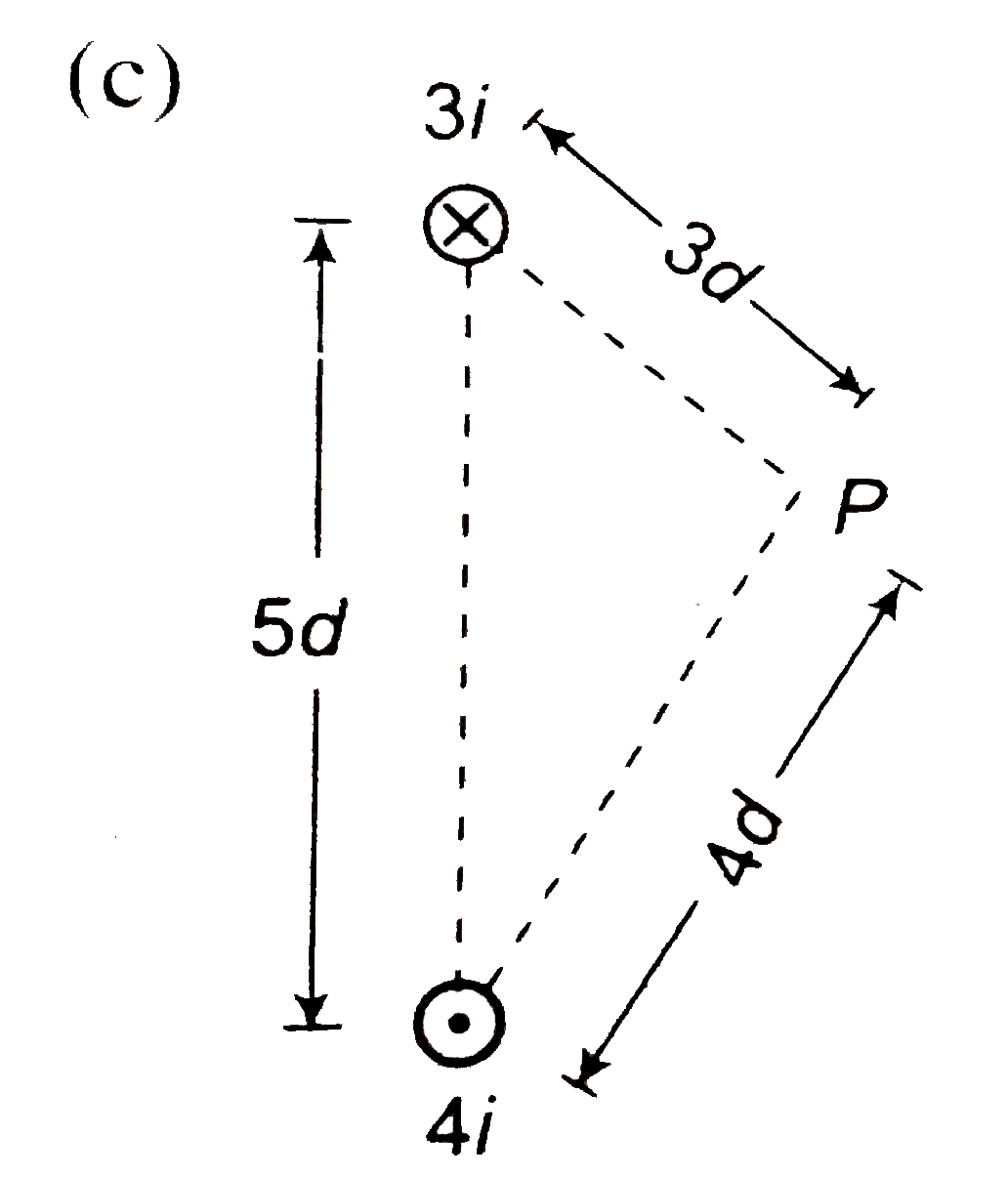
At what distance from left wire, magnetic field is zero on the line joining the wires.
Find magnitude of magnetic field at P.
(d) Two straight infinitely long and thin parallel wires are spaced d distance apart and carry a current i each. find the magnetic field at a point distance d from both wires when the currents are in the (i) same and (ii) opposite directions.
View Solution
Knowledge Check
Two long parallel wires are separated by a distance of 2m. They carry a current of 1A each in opposite direction. The magnetic induction at the midpoint of a straight line connecting these two wires is
AzeroB2×10−7TC4×10−5TD4×10−7TTwo infinitely long parallel wires carry equal current in same direction. The magnetic field at a mid point in between the two wires is
ATwice the magnetic field produced due to each of the wiresBHalf of the magnetic field produced due to each of the wiresCSquare of the magnetic field produced due to each of the wiresDZeroTwo infinitely long parallel wires carry equal currents in the same direction .The magnetic field at a mind point in between the two wires is
ASquare of the magnetic field produced due to each of the wiresBhalf of the magnetic field produced due to each of the wiresCtwice the magnetic field produced due to each of the wiresDzero
Two straight infinitely long and thin parallel wires are spaced 0.1m apart and carry a current of 10A each. Find the magnetic field at a point distance 0.1m from both wires in the two cases when the currents are in the (a) same and (b) opposite directions.
View SolutionTwo, current carrying conductors are placed parallel to each other. Explain if there is attraction or repulsion between them when the current flowing through them is in the.
(i) same direction
(ii) opposite direction.
View SolutionFind the force between two parallel conductors carrying currents (i) in the same direction (ii) in opposite directions and hence define one ampere.
View SolutionTwo long straight parallel current conductors are kept at a distance d from each other in air. The direction of current in both the conductors is the same. Find the magnitude and direction of the force between them. Hence, define one ampere.
View SolutionTwo long parallel current carrying conductors 30 cm apart having current each of 10 A in opposite direction, then value of magentic field at a point of 10 cm between them, from any of the wire.
View Solution

