A long straight wire carrying a current of 25A is placed in an external uniform magnetic field 3⋅0×10−4T parallel to the current. Find the magnitude of the resultant magnetic field at a point 1⋅5cm away from the wire.
The correct Answer is:4⋅48×10−4T
To find the magnitude of the resultant magnetic field at a point 1.5 cm away from a long straight wire carrying a current of 25 A in an external magnetic field of 3×10−4T, we can follow these steps:
Step 1: Identify the magnetic field due to the wire
The magnetic field B2 created by a long straight wire at a distance d from the wire can be calculated using the formula:
B2=μ0I2πd
Where:
- μ0=4π×10−7T m/A (permeability of free space)
- I=25A (current)
- d=1.5cm=0.015m
Step 2: Substitute the values into the formula
Substituting the values into the formula gives:
B2=4π×10−7×252π×0.015
Step 3: Simplify the expression
The π terms cancel out:
B2=4×10−7×252×0.015
Calculating the denominator:
2×0.015=0.03
Now substituting back:
B2=100×10−70.03
Step 4: Calculate B2
Calculating this gives:
B2=100×10−70.03=1003×10−5T≈3.33×10−5T
Step 5: Identify the external magnetic field
The external magnetic field B1 is given as:
B1=3×10−4T
Step 6: Determine the direction of the magnetic fields
- B1 is in the positive j direction.
- B2 due to the wire will be in the negative k direction (using the right-hand rule).
Step 7: Calculate the resultant magnetic field
Since B1 and B2 are perpendicular to each other, the magnitude of the resultant magnetic field BR can be calculated using the Pythagorean theorem:
BR=√B21+B22
Substituting the values:
BR=√(3×10−4)2+(3.33×10−5)2
Calculating each term:
(3×10−4)2=9×10−8
(3.33×10−5)2≈1.11×10−9
Now substituting back:
BR=√9×10−8+1.11×10−9≈√9.11×10−8≈3.02×10−4T
Final Result
The magnitude of the resultant magnetic field at a point 1.5 cm away from the wire is approximately:
BR≈3.02×10−4T
The magnetic field B2 created by a long straight wire at a distance d from the wire can be calculated using the formula:
- μ0=4π×10−7T m/A (permeability of free space)
- I=25A (current)
- d=1.5cm=0.015m
Substituting the values into the formula gives:
The π terms cancel out:
Calculating this gives:
The external magnetic field B1 is given as:
- B1 is in the positive j direction.
- B2 due to the wire will be in the negative k direction (using the right-hand rule).
Since B1 and B2 are perpendicular to each other, the magnitude of the resultant magnetic field BR can be calculated using the Pythagorean theorem:
(3.33×10−5)2≈1.11×10−9
The magnitude of the resultant magnetic field at a point 1.5 cm away from the wire is approximately:
Topper's Solved these Questions
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBook:PRADEEPChapter:MAGNETIC EFFECT OF CURRENT AND MAGNETISMExercise:Test Your Grip (a)
Explore 1 Video
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBook:PRADEEPChapter:MAGNETIC EFFECT OF CURRENT AND MAGNETISMExercise:Test Your Grip (c)
Explore 1 Video
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBook:PRADEEPChapter:MAGNETIC EFFECT OF CURRENT AND MAGNETISMExercise:Value Based Questions
Explore 2 Videos
- ELECTROSTATICSBook:PRADEEPChapter:ELECTROSTATICSExercise:ASSERTION-REASON TYPE QUESTIONS
Explore 2 Videos
- OPTICSBook:PRADEEPChapter:OPTICSExercise:Multiple choice questions
Explore 1 Video
Similar Questions
A long straight wire carrying a current of 20A is placed in an external uniform magnetic field of 3×10−4T parallel to the current. Find the magnitude of resultant field at a point 2⋅0cm away from the wire.
View SolutionA long, straight wire carrying a current of 1.0 A is placed horizontally in a uniform magnetic field B= (1.0×10−5) T pointing vertically upward. Find the magnitude of the resultant magnetic field at the points P and Q, both situated at a distance of 2.0 cm from the wire in the same horizontal plane.
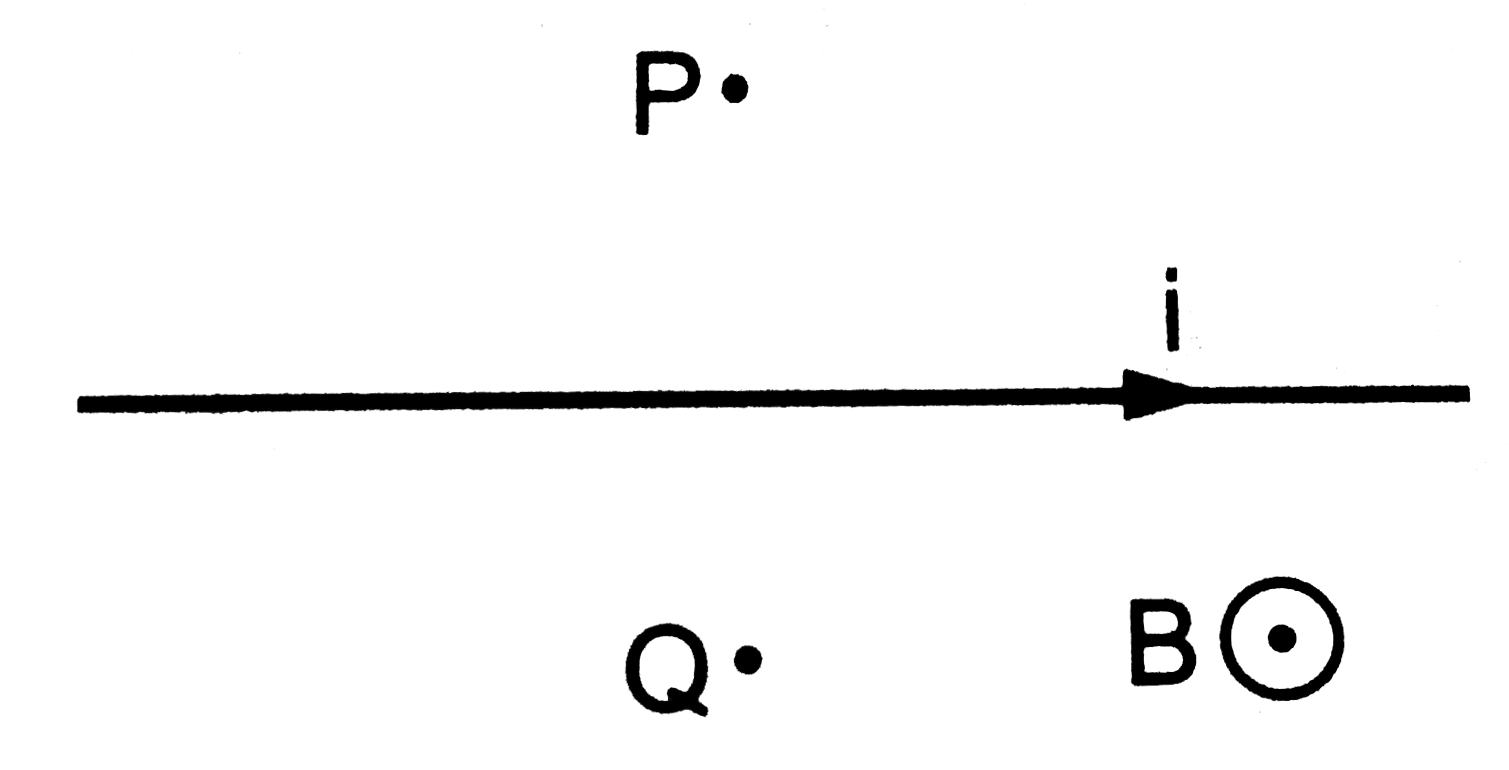
View Solution
Knowledge Check
A long straight wire carrying current of 30A is placed in an external unifrom magnetic field of induction 4×104T. The magnetic field is acting parallel to the direction of current. The maggnetic of the resultant magnetic inuduction in tesla at a point 2.0cm away form the wire is
A10−4B3×10−4C5×10−4D6×10−4A long straight wire carrying current of 30A is placed in an external uniform magnetic field of induction 4×104T. The magnetic field is acting parallel to the direction of current. The magnitude of the resultant magnetic inuduction in tesla at a point 2.0cm away form the wire is
A10−4B3×10−4C5×10−4D6×10−4A long straight wire carrying a current of 30 A is placed in an external unifom magnetic field of intensity 4×10−4 T. The magnetic field is acting parallel to the direction of current. The magnitude of the resultant magnetic induction in tesla at a point 2.0 cm away from the wire is (μ0=4π×10−7Hm−1)
A10−4B3×10−4C5×10−4D6×10−4
A long, straight wire carrying a current of 30 A is placed in an external uniform magnetic field of 4.0×10−4 T exists from south to north. Find at a point 2.0 away from the wire.
View SolutionA straight wire of1.4 m long carries a current of 7 A at right angles to a uniform magnetic field of 0.01 T. Calculate the mechanical force acting on the wire due to the magnetic field.
View SolutionA straight wire carrying a current of 5 A is bent into a semicircular arc of radius 2 cm as shown in the fig. Find the magnitude and direction of the magnetic field at the centre of the arc.

View SolutionA striaight wire carries a current of 3 A calculate the magnitude of the magentic field at a point 15 cm away from the wire
View SolutionIf a long straight wire carries a current of 40 A, then the magnitude of the field B at a point 15 cm away from the wire is
View Solution

