A regular polygon of n sides is formed by bending a wire of total length 2πr which carries a current i. (a) Find the magnetic field B at the centre of the polygon. (b) By letting n→∞ , deduce the expression for the magnetic field at the centre of a circular current.
The correct Answer is:B
a. 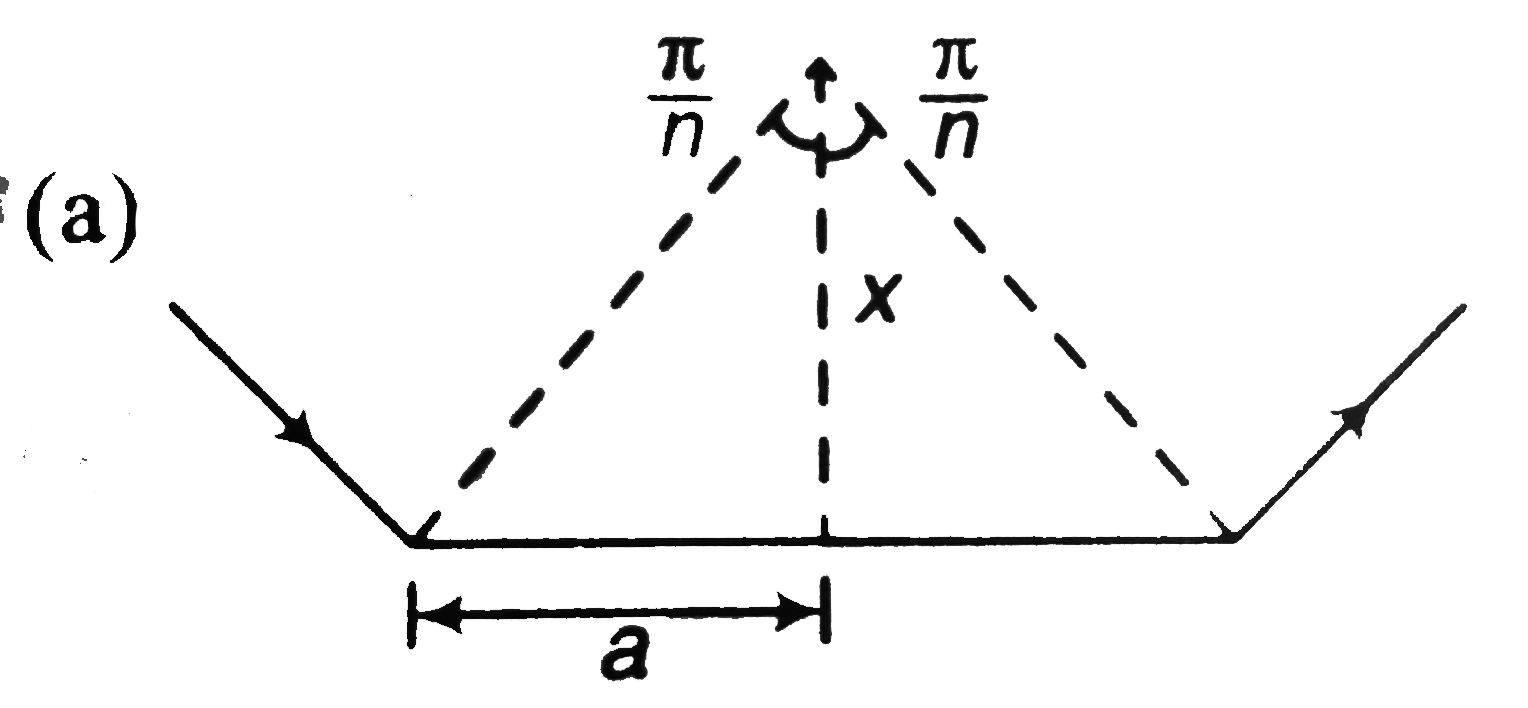
a=12(2πrn)=πrn
x=acotπn=(πrn)cot(πn)
B=n[μ04πix(sinπn+sinπn)]
=n[μ04πix(sinπn+sinπn)]
=n[μ04πi(πrn)cotπn(2sinπn)]
=μ2∈sin(πn)tan(πn)2πr
b. the above calculated magnetic field can be written is
B=μ0i2r(sinπnπn)2cosπn
Asn→∞πn→0
Hence,limπn→0(sinπnπn)→1
andlimπn→0(cotπn)→1
orB→μ0i2r
Topper's Solved these Questions
- MAGNETICSBook:DC PANDEYChapter:MAGNETICSExercise:INTRODUCTORY EXERCISE
Explore 1 Video
- MAGNETICSBook:DC PANDEYChapter:MAGNETICSExercise:SUBJECTIVE_TYPE
Explore 1 Video
- MAGNETICSBook:DC PANDEYChapter:MAGNETICSExercise:MCQ_TYPE
Explore 1 Video
- MAGNETIC FIELD AND FORCESBook:DC PANDEYChapter:MAGNETIC FIELD AND FORCESExercise:Medical entrance s gallery
Explore 59 Videos
- MAGNETISM AND MATTERBook:DC PANDEYChapter:MAGNETISM AND MATTERExercise:Medical gallery
Explore 1 Video
Similar Questions
A regular polygon of n sides is formed by bending a wire of length L which carries if the magnetic field B at the centre of the polygon μ0in2sinπntanπnNπL, then find the value of N
View SolutionA wire shaped to a regular hexagon of side 2cm carries a current of 2A. Find the magnetic field at the cetre of the hexagon.
View Solution
Knowledge Check
A square loop of side a carries a current I. The magnetic field at the center of the loop is
A2μ0I√2πaBμ0I√2πaC4μ0I√2πaDμ0IπaA square conducting loop of side length L carries a current I.The magnetic field at the centre of the loop is
Aindependent of LBproportional LCinversely proportional to LDlinearly proportional to LA rectangular loop of metallic wire is of length a and breadth b and carries a current i. The magnetic field at the centre of the loop is
Aμ0i4π8√a2+b2abBμ0i4π4√a2+b2abCμ0i4π2√a2+b2abDμ0i4π√a2+b2ab
Find the magnetic field induction at a point on the axis of a circular coil carrying current and hence find the magnetic field at the centre of circular coil carrying current.
View SolutionWhat is the direction of magnetic field at the centre of a current- carrying circular loop?
View SolutionWhat is the direction of magnetic field at the centre of a current- carrying circular loop?
View SolutionFind the magnetic field B at the centre of a rectangular loop of length l and width b, carrying a current i.
View SolutionA wire of length L carrying a current I is bent into a circle. The magnitude of the magnetic field at the centre of the circle is
View Solution

