The figure shows tow coaxial circulalr loop a1 and 2, which forms same solid angle θ at point O. If B1 and B2 are the magnetic fields produced at the point O due to loop 1 and 2 respectively, then

B1B2=1
B1B2=2
B1B2=8
B1B2=4
The correct Answer is:B
B1=μIR32(R2+x2)32
B2=μI(2R)22[(2R)2+(2x)2]32
B1B2=2
Topper's Solved these Questions
- MAGNETICSBook:DC PANDEYChapter:MAGNETICSExercise:INTRODUCTORY EXERCISE
Explore 1 Video
- MAGNETICSBook:DC PANDEYChapter:MAGNETICSExercise:SUBJECTIVE_TYPE
Explore 1 Video
- MAGNETICSBook:DC PANDEYChapter:MAGNETICSExercise:MCQ_TYPE
Explore 1 Video
- MAGNETIC FIELD AND FORCESBook:DC PANDEYChapter:MAGNETIC FIELD AND FORCESExercise:Medical entrance s gallery
Explore 59 Videos
- MAGNETISM AND MATTERBook:DC PANDEYChapter:MAGNETISM AND MATTERExercise:Medical gallery
Explore 1 Video
Similar Questions
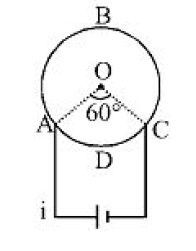
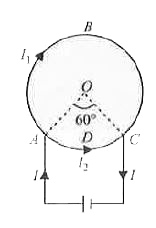
A cell is connected between the points A and C of a circular conductor ABCD of centre 'O'.∠AOC=60∘. IfB1andB2 are the magnitudes of the magnetic fields at O due to the currents in ABC and ADC respectively, the ratio B1B2, is
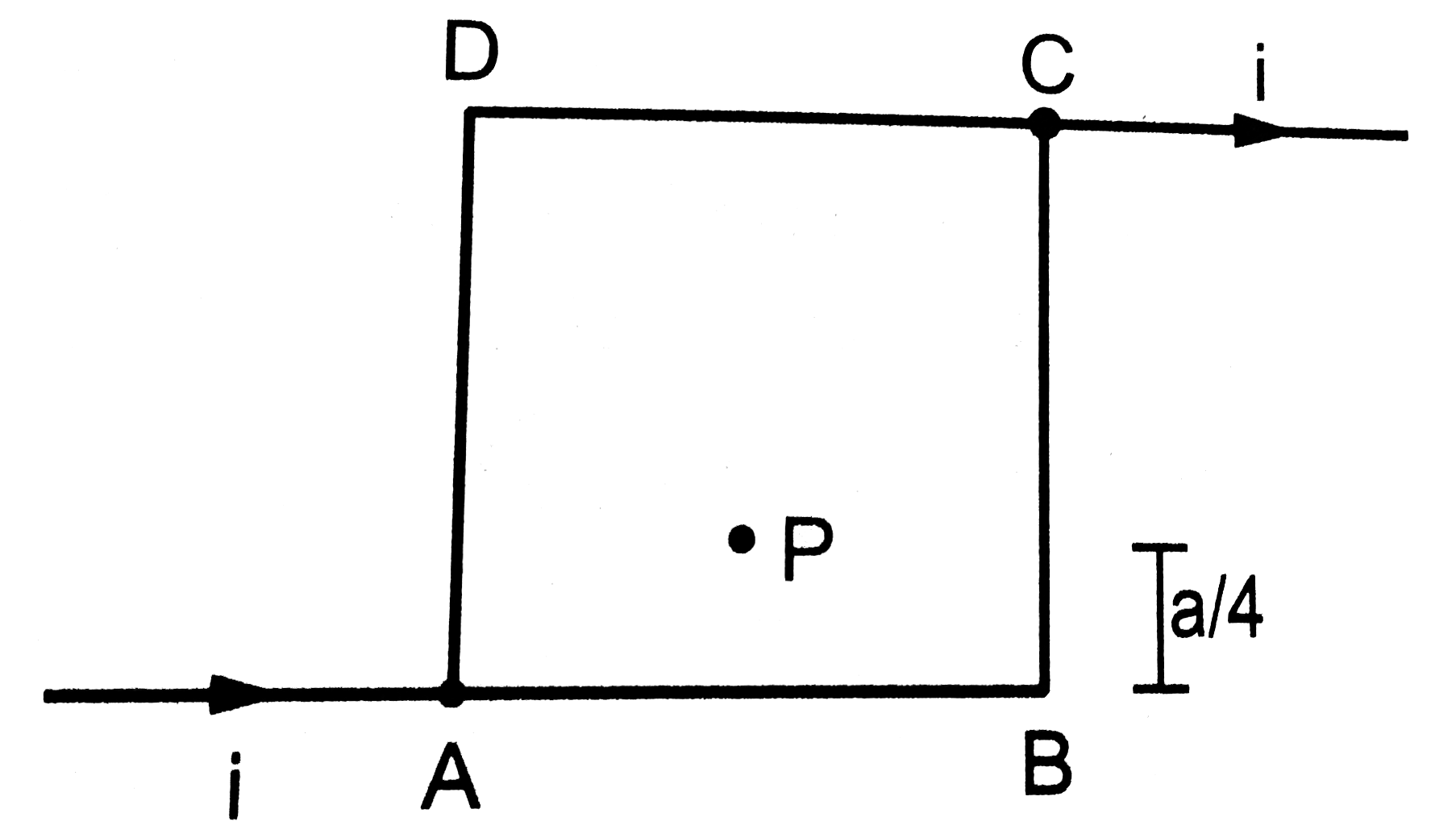
View SolutionFigure shows a square loop of edge a made of a uniform wire. A current i enters the loop at the point A and leaves it at the point C. Find the magnetic field at the point P which is on the perpendicular bisector of AB at a distance a/4 from it.
View Solution
Knowledge Check
A straight wire and a circular loop both carrying currents are in the same vertical plane. There is no contact between the two at the point A. If B1 and B2 are magnetic fields due to i1andi2 respectively at the point C, the centre of the loop, then the total field at C is:
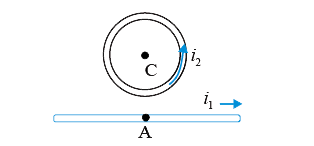 AZeroB(B1−B2)or(B2−B1)C(B1+B2) perpendicular to the plane of the loop towards usD(B1+B2) perpendicular to the plane of the loop away from us
AZeroB(B1−B2)or(B2−B1)C(B1+B2) perpendicular to the plane of the loop towards usD(B1+B2) perpendicular to the plane of the loop away from usA current - carrying loop is shown in the figure. The magnitude of the magnetic field produced at a point O is
 Aμ0I4RBμ0I2R(1+√2π)Cμ0I4R(1+√2π)Dμ04R(1+2√2π)
Aμ0I4RBμ0I2R(1+√2π)Cμ0I4R(1+√2π)Dμ04R(1+2√2π)Magnetic field produced at the point O due to current flowing in an infinite wire shaped as shown in the figure is
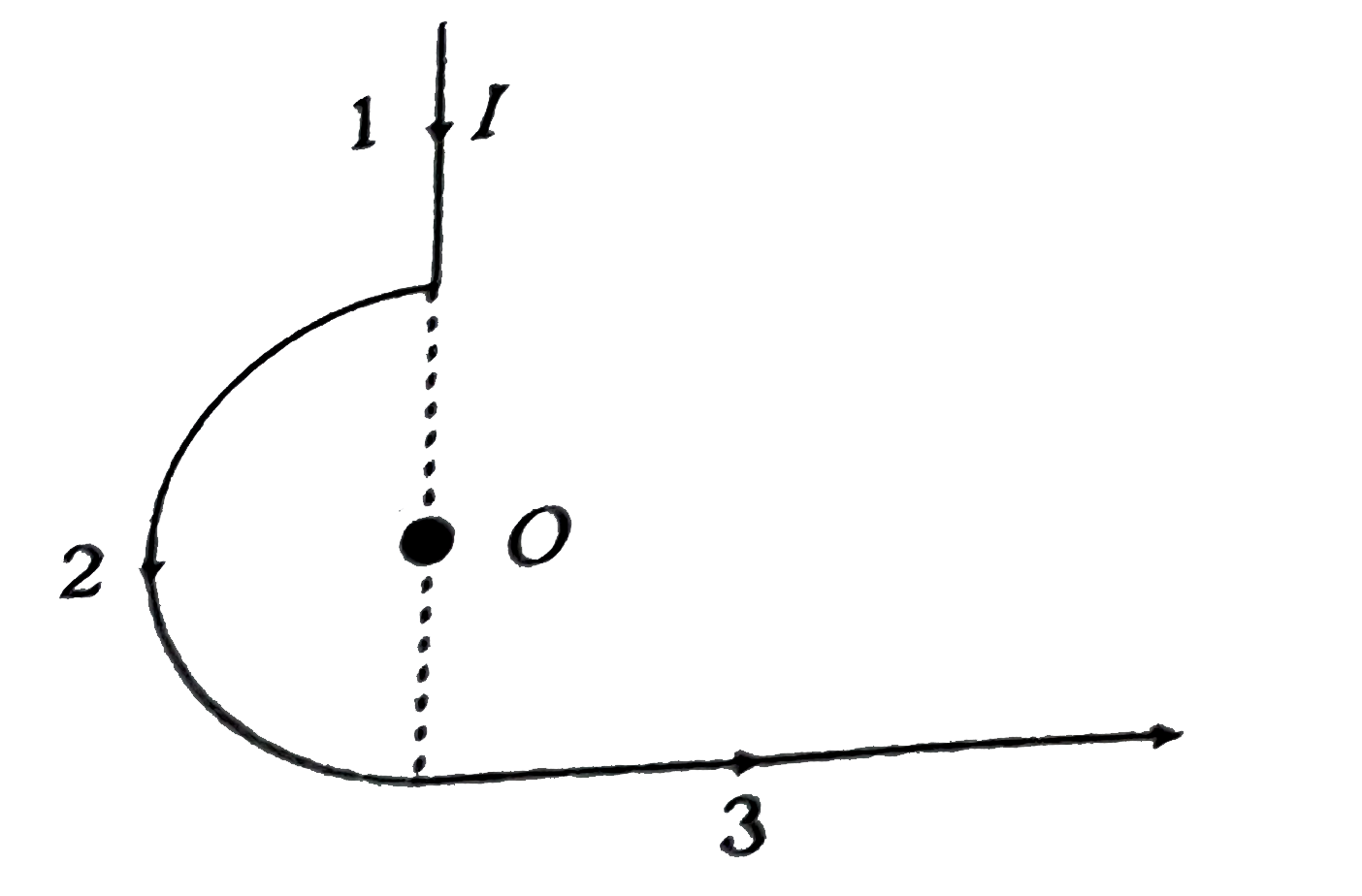 Aμ0I4πRBμ0I4R−μ0I4πRCμ0I4R−μ0I2πRDμ0I4R+μ0I4πR
Aμ0I4πRBμ0I4R−μ0I4πRCμ0I4R−μ0I2πRDμ0I4R+μ0I4πR
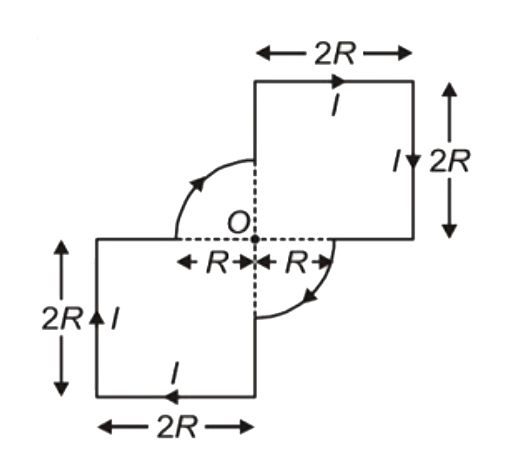
The magnitude of the magnetic field (B) due to loop ABCD at the origin (O) is

View SolutionThe figure shows the cross section of two long coaxial tubes carrying equal current I in opposites directions. If B1 and B2 are magnetic fields at point 1 and 2 as shown in figure then

View SolutionA cell is connected between the points A and Cofa circular conductor ABCDA of centre O. ∠AOC=60∘. If B1, and B2, are the magnitudes of the magnetic fields at O due to currents in ABC and ADC respectively, the ratio B1/B2, is
View SolutionIn the figure shown a semicircular wire loop is placed in a uniform magnetic field B=1.0T. The plane of the loop is perpendicular to the magnetic field. Current i=2A flows in the loop in the directions shown. Find the magnitude of the magnetic force in newton in both the cases a and b. The radius of the loop is 1.0 m

View SolutionThe figure shows three indentical current carryng square loops A,B and C. Identify the correct statement related to magnetic field B at the centre O of the square loop. Current in each wire is I.

View Solution

