A particle of mass m and charge q is accelerated by a potential difference V volt and made to enter a magnetic field region at an angle θ with the field. At the same moment, another particle of same mass and charge is projected in the direction of the field from the same point. Magnetic field induction is B. What would be the speed of second particle so that both particles meet again and again after regular interval of time. Also, find the time interval after which they meet and the distance travelled by the second particle during that interval.
√Vmq2πBcosθ
√2Vm3q2πBcosθ
√2Vmq2πBcosθ
23√Vmqπmcosθ
The correct Answer is:c
The first parallel will have a helical path and the second particle will move rectilinearly along the field. For the two particles to meet again and again,
V∣∣T=v'T
where v' is the speed of the second
particle.
∴v'=v∣∣=vcosθ
12mv2=qV⇒v=√2qVm
∴v'=√2qVmcosθ
T=2πmqB
Distance travelled =pitch
Distance =√2qVmcosθ×2πmqB
Distance =√2Vmq2πBcosθ
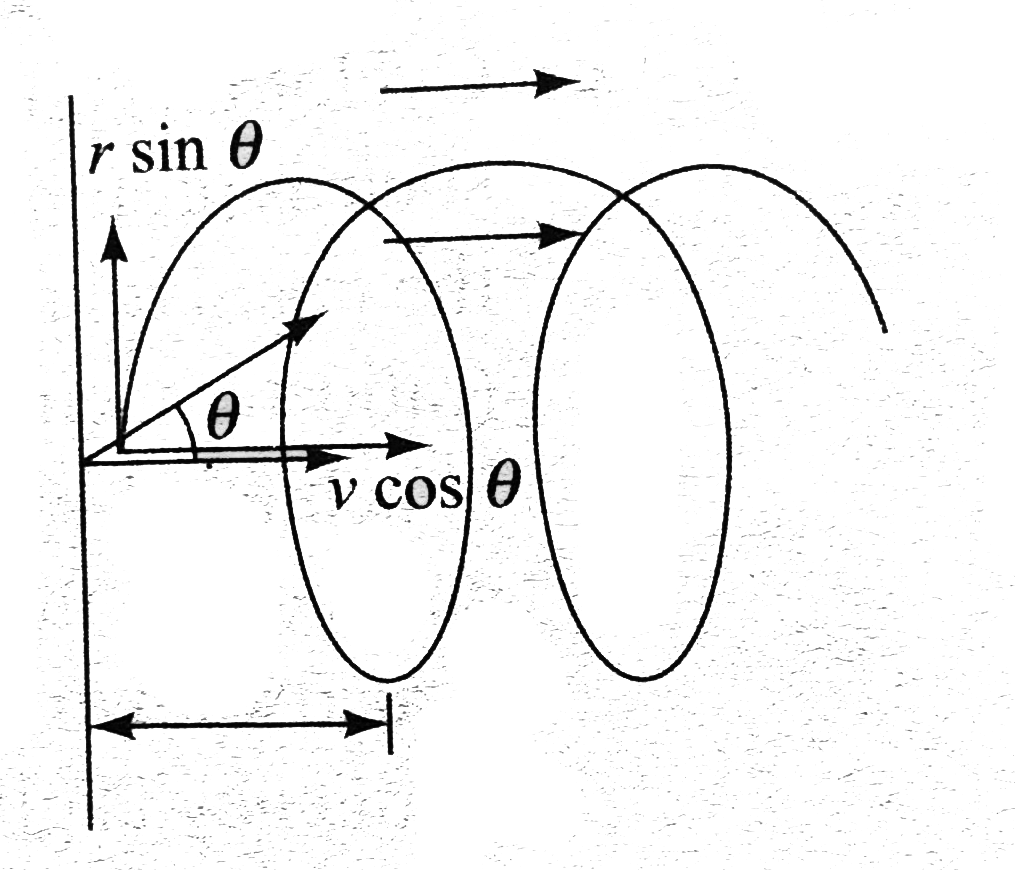 .
.
Topper's Solved these Questions
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICSCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercises Integer
7 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICSCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Archives Fill In The Blank
6 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICSCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercises Assertion -reasoning
8 Videos
- KINETIC THEORYBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORYEXERCISE - Question Bank
31 Videos
- Magnetism and MatterBOOK - CENGAGE PHYSICSCHAPTER - Magnetism and MatterEXERCISE - Question Bank
50 Videos
Similar Questions
A charge particle of mass m and charge q is accelerated by a potential difference V volt. It enters in a region of uniform magnetic field Bas shown in figure-4.93. Find the time after which it will come out from the magnetic field.

View SolutionA charged particle of mass m and charge q is accelerated through a potential difference of V volts. It enters a region of uniform magnetic field which is directed perpendicular to the direction of motion of the particle. Find the radius of circular path moved by the particle in magnetic field.
View Solution
Knowledge Check
A charged particle enters a magnetic field at an angle of 90∘with the magnetic field. The path of the particle will be a/an
AHelixBEllipseCCircleDStraight lineA particle of mass m carrying charge q is accelerated by a potential difference V. It enters perpendicularly in a region of uniform magnetic field B and executes circular arc of radius R, then qm equals
A2VB2R2BV2BRCVB2RDmVBRA charged particle of mass m and charge q is accelerated through a potential differences of V volts. It enters of uniform magnetic field B which is directed perpendicular to the direction of motion of the particle. The particle will move on a circular path of radius
A(√Vm2qB2)B2VmqB2C√2Vmq(1B)D√Vmq(qB)
A charged particle having mass m and charge q is accelerated by a potential difference V, it flies through a uniform transverse magnetic field B. The field occupies a region of space d. Fnd the time interval for which it remains inside the magnetic field.
View SolutionA charged particle of charge q and mass m is shot into a uniform magnetic field of induction B at an angle θ with the field. The frequency of revolution of the particle
View SolutionA charged particle, having charge q1 accelerated through a potential difference V enter a perpendicular magnetic field region in which it experiences a force F. If V is increased to 5V, the particle will experience a force
View SolutionA particle of mass 'm' and charge 'Q' is acceleration in cyclotron. If magnetic field is 'B' and radius cyclotron is r then find the kinetic energy of particle.
View SolutionPositively charged particles are projected into a magnetic field. If the direction of the magnetic field is along the direction of motion of the charged particles, the particles get
View Solution
