A charged particle carrying charge q=10μC moves with velocity v1=106,s−1 at angle 45∘ with x-axis in the xy plane and experience a force F1=5√2mN along the negative z-axis. When the same particle moves with velocity v2=106ms−1 along the z-axis, it experiences a force F2 in y-direction.
Find the magnitude of the force F2.
10−2N
10−3N
10−4N
10−5N
The correct Answer is:a
To solve the problem, we will follow these steps:
Step 1: Understand the Given Information
We have a charged particle with:
- Charge q=10μC=10×10−6C
- Velocity v1=106m/s at an angle of 45∘ with the x-axis in the xy-plane.
- Force F1=5√2mN=5√2×10−3N acting along the negative z-axis.
Step 2: Convert Velocity into Components
The velocity v1 can be broken down into its x and y components:
- v1x=v1cos(45∘)=106⋅1√2=5×105m/s
- v1y=v1sin(45∘)=106⋅1√2=5×105m/s
Thus, we can write:
v1=(5×105^i+5×105^j)m/s
Step 3: Use the Lorentz Force Equation
The force experienced by a charged particle in a magnetic field is given by:
F=q(v×B)
Given that F1 acts in the negative z-direction, we can express this as:
F1=5√2×10−3^kN
Step 4: Find the Magnetic Field B
From the equation F1=q(v1×B), we can rearrange it to find B:
B=F1q⋅v1
Step 5: Calculate the Magnitude of the Magnetic Field
Using the magnitude of F1:
|F1|=5√2×10−3N
Substituting the values:
B=5√2×10−310×10−6⋅106=5√2×10−310×10−6⋅106=10−3T^i
Step 6: Analyze the Second Situation
Now, when the particle moves with velocity v2=106m/s along the z-axis, we have:
v2=106^km/s
Step 7: Calculate the Force F2
Using the Lorentz force equation again:
F2=q(v2×B)
Substituting the values:
F2=10×10−6⋅(106^k×10−3^i)
Step 8: Perform the Cross Product
Using the right-hand rule:
^k×^i=−^j
Thus:
F2=10×10−6⋅10−3(−^j)=−10−8^jN
Step 9: Find the Magnitude of F2
The magnitude of F2 is:
|F2|=10−8N
Final Answer
The magnitude of the force F2 is 10−8N.
---
We have a charged particle with:
- Charge q=10μC=10×10−6C
- Velocity v1=106m/s at an angle of 45∘ with the x-axis in the xy-plane.
- Force F1=5√2mN=5√2×10−3N acting along the negative z-axis.
The velocity v1 can be broken down into its x and y components:
- v1x=v1cos(45∘)=106⋅1√2=5×105m/s
- v1y=v1sin(45∘)=106⋅1√2=5×105m/s
v1=(5×105^i+5×105^j)m/s
The force experienced by a charged particle in a magnetic field is given by:
F=q(v×B)
Given that F1 acts in the negative z-direction, we can express this as:
F1=5√2×10−3^kN
From the equation F1=q(v1×B), we can rearrange it to find B:
B=F1q⋅v1
Using the magnitude of F1:
|F1|=5√2×10−3N
Substituting the values:
B=5√2×10−310×10−6⋅106=5√2×10−310×10−6⋅106=10−3T^i
Now, when the particle moves with velocity v2=106m/s along the z-axis, we have:
v2=106^km/s
Using the Lorentz force equation again:
F2=q(v2×B)
Substituting the values:
F2=10×10−6⋅(106^k×10−3^i)
Using the right-hand rule:
^k×^i=−^j
Thus:
F2=10×10−6⋅10−3(−^j)=−10−8^jN
The magnitude of F2 is:
|F2|=10−8N
The magnitude of the force F2 is 10−8N.
Topper's Solved these Questions
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICSCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercises Integer
7 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICSCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Archives Fill In The Blank
6 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICSCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercises Assertion -reasoning
8 Videos
- KINETIC THEORYBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORYEXERCISE - Question Bank
31 Videos
- Magnetism and MatterBOOK - CENGAGE PHYSICSCHAPTER - Magnetism and MatterEXERCISE - Question Bank
50 Videos
Similar Questions
A charged particle carrying charge q=1μc moves in uniform magnetic with velocity v1=106m/s at angle 45∘ with x-axis in the xy-plane and experiences a force F1=5√2mN along the negative z-axis. When te same particle moves with velocity v2=106m/s along the z-axis it experiences a force F2 in y-direction. Find
a. the magnitude and direction of the magnetic field
b. the magnetic of the force F2.
View SolutionA particle having charge q=10μC is moving with a velocity of V=106m/sin a direction making an angle of 45° with positive x axis in the xy plane (see figure). It expe- riences a magnetic force along negative z direction. When the same particle is projected with a velocity v'=106m/sin positive z direction, it experiences a magnetic force of 10 mN along X direction. Find the direction and magnitude of the magnetic field in the region.
View Solution
Knowledge Check
A charged particle carrying charge q=10μC moves with velocity v1=106,s−1 at angle 45∘ with x-axis in the xy plane and experience a force F1=5√2mN along the negative z-axis. When the same particle moves with velocity v2=106ms−1 along the z-axis, it experiences a force F2 in y-direction.
Find the magnetic field →B.A(10−3T)(ˆi+ˆj)B(2×10−3T)ˆiC(10−3T)ˆiD(2×10−3T)(ˆi+ˆj)A particle of charge −16×10−18coo–mb moving with velocity 10ms−1 along the x−aξs, and an electric field of magnitude (104)/(m) is along the negative z−ais. If the charged particle continues moving along the x−aξs , the magnitude of B is
A(103Wb)/(m2)B(105Wb)/(m2)C(1016Wb)/(m2)D(10−3Wb)/(m2)A charge q is moving with a velocity v1=1ˆi m/s at a point in a magentic field and experiences a force F=q[−ˆj+1ˆk] N. If the charge is moving with a voloctiy v2=2ˆj m/s at the same point then it experiences a force F2=q(1ˆi−1ˆk) N. The magnetic induction B at that point is
A(ˆl+ˆj+ˆk)wb/m2B(ˆl−ˆj+ˆk)wb/m2C(−ˆl+ˆj−ˆk)wb/m2D(ˆl+ˆj−ˆk)wb/m2
A particle of charge −16×10−19C moving with velocity 10mg−1 along the x -axis ẹnters a region where magnetic field B is along the y axis and electric field of magnitude 104 (V/m) is along the negalive z-axis If the charged particle contintes moving along the x -axis, then the magnitude of B(Wb(m)2) is
View SolutionAt t=0, the particle is at the origin and its velocity is 10m/s at an angle 37∘ with the x-axis. The particle moves in x−y plane with a constant acceleration of 1m/s2 along the y-axis. Find the magnitude and direction of the velocity after 2s.
View SolutionA particle moving with speed v0=10√2ms−1 strikes a wall at an angle 45∘ as shown in figure. Find magnitude of change in velocity.
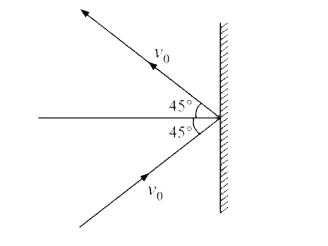
View SolutionA particle of charge −1.6×10−19C moving with velocity 10ms−1 along the X-axis enters a region of magnetic field of induction B along V-axis and an electric field of strength 104V/m along negative Z-axis. If the charged particle continues to move along the X-axis, the magnitude of B is
View SolutionA charged particle of charge q moving with the velocity v, enters along the axis of a solenoid carrying a current. If B is the magnetic induction along the axis of the solenoid then the force acting on the charged particle will be
View Solution
