The region between x=0 and x=L is filled with uniform constant magnetic field 25(T)ˆk. A particle of mass m=50g having positive charge q=1C and velocity →V0=50√3ˆi+50ˆjms−1 enters the region of the magnetic field. Neglect gravity throughout the question.

The maximum and minimum values of L such that velocity of emerging particle makes angle π/3 with the y-axis are
Lmin=10cm,Lmax=∞
Lmin=20cm,Lmax=40cm
Lmin=10cm,Lmax=20cm
Lmin=20cm,Lmax=∞
The correct Answer is:d
sin30∘=L/R
L=mV02qB=50×10−3×1002×1×25=110m=10cm

L=AB+BC
=rcos60∘+rcos60∘=r
L=mV0qB=20cm
⇒ This is minimum L.
For other case:
For this case L can extend upto ∞.

Topper's Solved these Questions
- MAGNETIC FIELD AND MAGNETIC FORCESBook:CENGAGE PHYSICSChapter:MAGNETIC FIELD AND MAGNETIC FORCESExercise:Exercises Integer
Explore 7 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBook:CENGAGE PHYSICSChapter:MAGNETIC FIELD AND MAGNETIC FORCESExercise:Archives Fill In The Blank
Explore 6 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBook:CENGAGE PHYSICSChapter:MAGNETIC FIELD AND MAGNETIC FORCESExercise:Exercises Assertion -reasoning
Explore 8 Videos
- KINETIC THEORYBook:CENGAGE PHYSICSChapter:KINETIC THEORYExercise:Question Bank
Explore 31 Videos
- Magnetism and MatterBook:CENGAGE PHYSICSChapter:Magnetism and MatterExercise:Question Bank
Explore 50 Videos
Similar Questions
The region between x=oandx=L is filled with uniform, steady magnetic field B0ˆk. A particle of mass m , positive charge q and velocity v0ˆi travels along x−aξs and enters the region of the magnetic field. Neglect gravity throughout the question .
(a) Find the value of L if the particle emerges from the region of magnetic field with its final velocity at angle 30∘ to its initial velocity.
(b) Find the velocity of the particle and the time spent by it in the magnetic field, if the magnetic field now extends upto 2.1L.
View SolutionThe region between x=0 and x=L is filled with uniform steady magnetic field B0ˆk. A particle of mass m, positive charge q and velocity v0ˆi travels along x-axis and enters the region of the magnetic field. Neglect the gravity throughout the question.
a. Find the value of l if the particle emerges from the region of magnetic field with its final velocilty at an angel 30∘ to its initial velocity.
b. Find the final velocity of the particle and the time spent by it in the magnetic field, if themagnetic field now extends upto 2.1L.
View Solution
Knowledge Check
The region between x=0 and x=L is filled with uniform constant magnetic field 25(T)ˆk. A particle of mass m=50g having positive charge q=1C and velocity →V0=50√3ˆi+50ˆjms−1 enters the region of the magnetic field. Neglect gravity throughout the question.
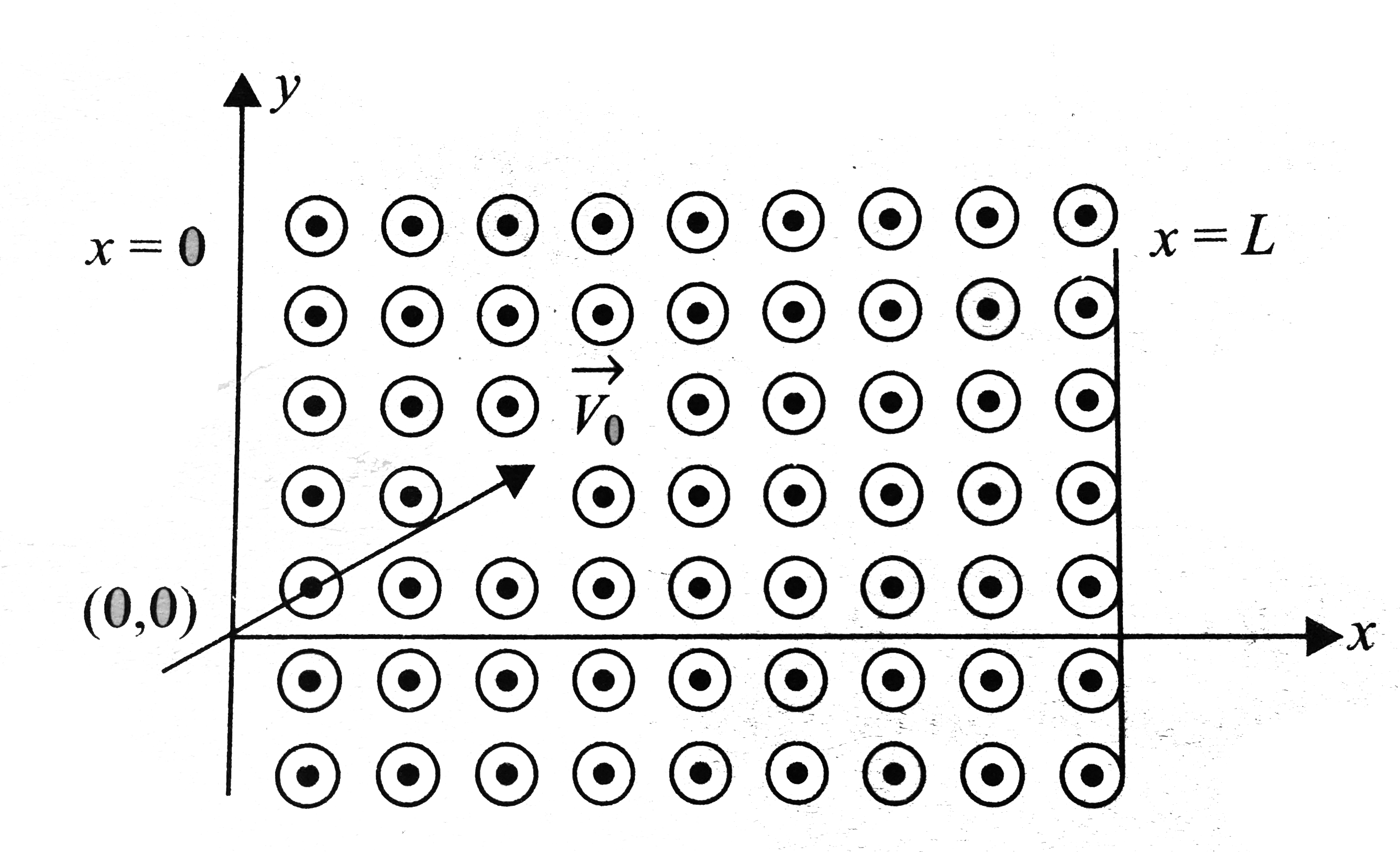
The value of L if the particle emerges from the region of magnetic field with its velocity 100(ms−1)ˆi isA20cmB10cmC30cmDNone of theseA particle of charge q and mass m moving with a velocity v along the x-axis enters the region x>0 with uniform magnetic field B along the ˆk direction. The particle will penetrate in this region in the x-direction upto a distance d equal to
AZeroBmvqBC2mvqBDinfinityA particle of the mass m and cgharge q moves with a constant velocity v along the positive x−direction.Itentersaregionconta∈∈gauniformmag≠ticfieldBdirectedalongtheminiμmvalueofvrequiredsotˆthepartic≤canjustentertheregion xgtb is
AqbBmBq(b−A)BmCqaBmDq(b+a)B2m
A particle of mass m and charge q moving with velocity v enters the region of uniform magnetic field at right angle to the direction of its motion. How does its kinetic energy get affected?
View SolutionThe region between y =0 and y=d constains a magnetic field →B=B→z. A particle of mass m and charge q enters of the region with a velocity →v=v→i. If d=mv2qB the acceleration of the charged particle at the point of its emergence at the other side is :
View SolutionA positive charge particle having change q and mass m has velocity →v=v(ˆi+ˆk√2) in the magnetic field B at the origin . Its speed as the function of y is :
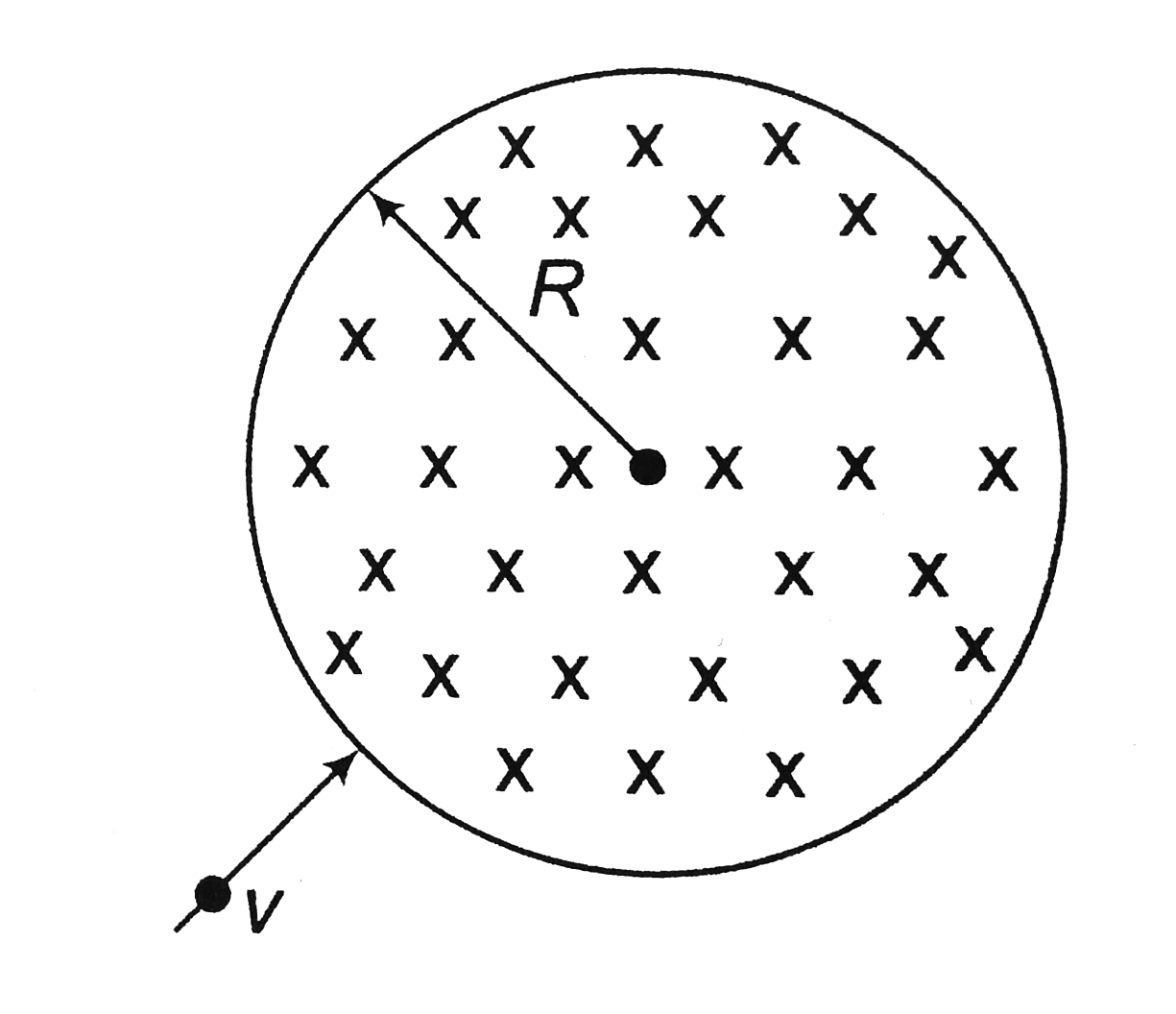
View SolutionA particle of mass m having a charge q enters into a circular region of radius R with velocity v directed towards the centre. The strength of magnetic field is B. Find the deviation in the path of the particle.
View SolutionIn a certain region, uniform electric field E=−E0ˆk and magnetic field B=B0ˆk are present. At time t=0, a particle of mass in and charge q is given a velocity v=v−0ˆj+v−0ˆk. Find the minimum speed of the particle and the time when it happens so.

View Solution
