A wire carrying a 10A current is bent to pass through various sides of a cube of side 10 cm as shown in fig. A magnetic field →B=(2ˆi−3ˆjˆk)T is present in the region.

Find the magnetic moment vector of the loop.
(0.1ˆi+0.05ˆj−0.05ˆk)Am2
(0.1ˆi+0.05ˆj+0.05ˆk)Am2
(0.1ˆi−0.05ˆj+0.05ˆk)Am2
(0.1ˆi−0.05ˆj−0.05ˆk)Am2
The correct Answer is:b
The net force on a current carrying loop of any arbitrary
shope in a uniform magnetic field is zero.
→Fnet=0
The given loop can be considered to be a superposition of three
loops as shown in Fig. The area vector of the three loops
(1) ,(2) and (3) are

→A1=(12×10×10×10−4)ˆjm2
→A2=(12×10×10×10−4)ˆkm2
→A3=(12×10×10×10−4)ˆim2
Magnetic moment vector,
→μ=i→A=10(0.01ˆi+0.005ˆj+0.005ˆk)Am2
=(0.1ˆi+0.05ˆj+0.05ˆk)Am2
Torque,
→τ=(0.1ˆi+0.05ˆj+0.05ˆk)×(2ˆi−3ˆj+ˆk)
∣∣
∣
∣∣ˆiˆjˆk0.10.050.052−31∣∣
∣
∣∣=0.2ˆi−0.4ˆkNm
Topper's Solved these Questions
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICSCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercises Integer
7 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICSCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Archives Fill In The Blank
6 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICSCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercises Assertion -reasoning
8 Videos
- KINETIC THEORYBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORYEXERCISE - Question Bank
31 Videos
- Magnetism and MatterBOOK - CENGAGE PHYSICSCHAPTER - Magnetism and MatterEXERCISE - Question Bank
50 Videos
Similar Questions
A wire carrying a 10 A current is bent to pass through sides of a cube of side 10 cm as shown in figure. A magnetic field →B=(2ˆi−3ˆj+ˆk)T is present in the region. Then, find
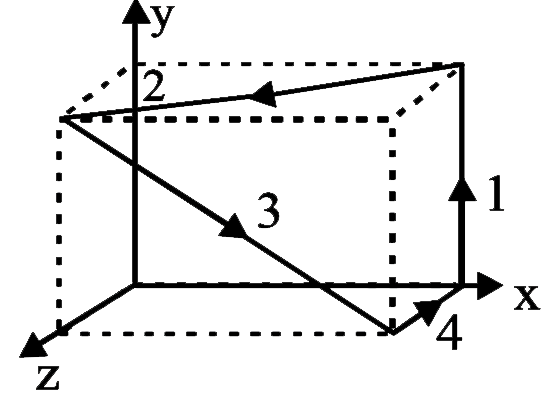
The magnetic moment vector of the loop.
View SolutionA wire carrying a 10 A current is bent to pass through sides of a cube of side 10 cm as shown in figure. A magnetic field →B=(2ˆi−3ˆj+ˆk)T is present in the region. Then, find
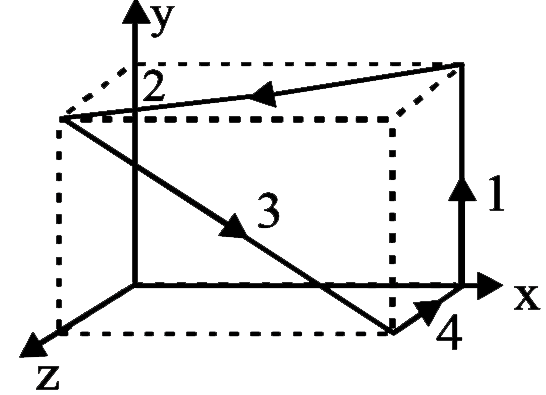
The net force on the loop
View Solution
Knowledge Check
A wire carrying a 10A current is bent to pass through various sides of a cube of side 10 cm as shown in fig. A magnetic field →B=(2ˆi−3ˆjˆk)T is present in the region.

Find the net torque on the loop.A−0.1ˆi+0.4ˆkNmB−0.1ˆi−0.4ˆkNmC0.2ˆi−0.4ˆkNmD0.1ˆi−0.4ˆkNmA wire carrying a 10A current is bent to pass through various sides of a cube of side 10 cm as shown in fig. A magnetic field →B=(2ˆi−3ˆjˆk)T is present in the region.

Find the net force on the loop shown.A→Enet=0B→Enet=(0.1ˆi−0.2ˆk)NC→Enet=(0.3ˆi+0.4ˆk)ND→Enet=(0.36ˆk)N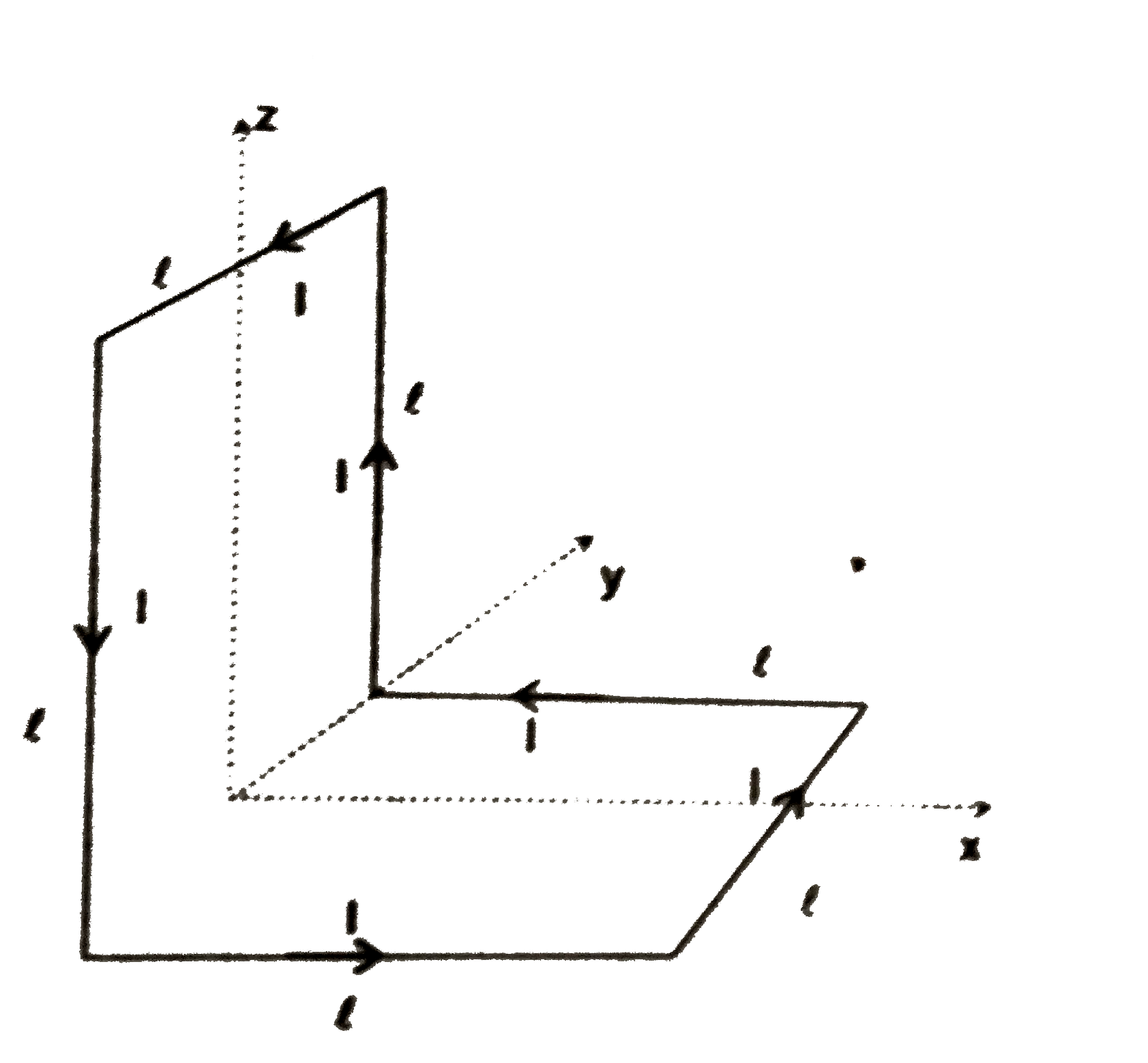
A conducting loop carrying current 'l' is bent into two halves and placed in mutually perpendicular planes xy and yz planes as shown. A uniform magnetic field →B=Bˆj is existing in the region. The net magnetic torque experienced by the loop isABIl2(ˆk−ˆi)BBIl2(ˆi+ˆj)CBIl2(ˆj+ˆk)DBIl2(ˆi+ˆk)
A wire carrying a 10 A current is bent to pass through sides of a cube of side 10 cm as shown in figure. A magnetic field →B=(2ˆi−3ˆj+ˆk)T is present in the region. Then, find
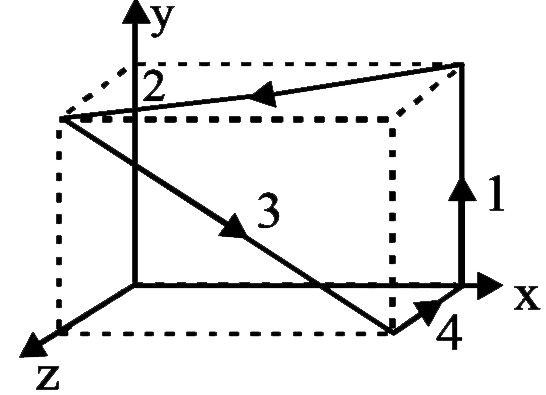
The net torque on the loop
View SolutionA wire of length l metre carries a current I ampere along the Y-axis. A magnetic field, →B=B0(ˆi+ˆj+ˆk) tesla exists in space. Find the magnitude of the force on the wire.
View SolutionA square loop of side l carries a current i. it is placed as shown in figure. Find the magnetic moment of the loop.
View Solution
A conducting wire MN carrying a current I is bent into the shape as shown and placed in xy plane. A uniform magnetic field →B=−Bˆk is existing in the region. The net magnetic force experenced by the conducting wire MN is
View SolutionA straight wire carrying a current 10A is bent into a semicircular arc of radius 5cm. The magnitude of magnetic field at the center is
View Solution
