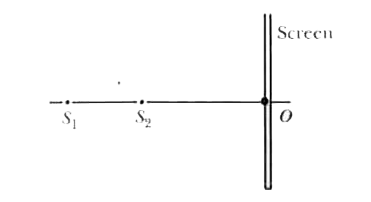
In figure, a screen is placed normaol to the line joining the two point coherent sources S1 and S2. The interference pattern consists of concentric circles.

Find the radius of the nth bright ring
D√1(1−nλd)
D√2(1−nλd)
2D√2(1−nλd)
D√2(1−nλ2d)
The correct Answer is:b
The optical path difference at P is
Δx=S1P−S2P=cosθ
∵cosθ=1−θ22 for small θ
∴Δx=d(1−θ22)
=d[1−y22D2], where D+d=D
For nth maxima,
⇒Δx=nλ
d[1−y22D2]=nλ
y = radius of the nth brigth ring
=D√2(1−nλd)
At the central maxima, θ=0
Δx=d=nλ
⇒n=dλ=0.50.5×10−3=1000
Hence, for the closest second brigth ring, n=998.
Putting values, r=6.32cm.
Topper's Solved these Questions
- WAVE OPTICSBook:CENGAGE PHYSICSChapter:WAVE OPTICSExercise:Integer
Explore 3 Videos
- WAVE OPTICSBook:CENGAGE PHYSICSChapter:WAVE OPTICSExercise:Archives
Explore 4 Videos
- WAVE OPTICSBook:CENGAGE PHYSICSChapter:WAVE OPTICSExercise:Assertion- Reasoning
Explore 13 Videos
- THERMODYNAMICSBook:CENGAGE PHYSICSChapter:THERMODYNAMICSExercise:QUESTION BANK
Explore 34 Videos
- WAVESBook:CENGAGE PHYSICSChapter:WAVESExercise:QUESTION BANK
Explore 38 Videos
Similar Questions
In the figure shown, a screen is placed normal to the line joining the two point coherent sources S1andS2. The interference pattern consists of concentric circles.
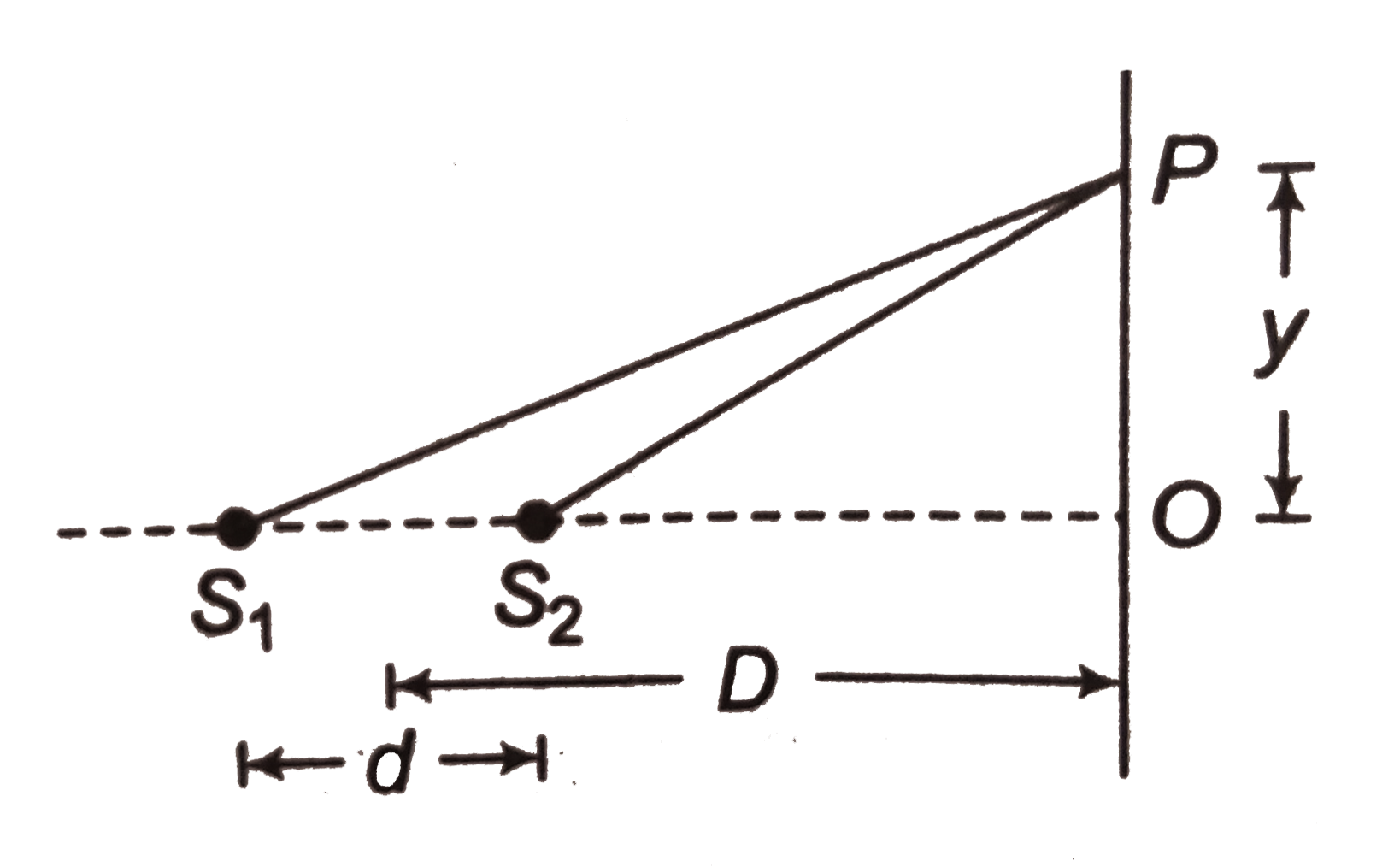
(a)Find the radius of the nth bright ring.
(b) If d=0.5 mm, λ=5000Å and D=100 cm, find the radius of the closest second bright ring.
(c) Also, find the value of n for this ring.
View SolutionTwo point sources are d=nλ apart. A screen is held at right angles to the line joining the two sources at a distance D from the nearer source. Calculate the distance of the point on the screen where the first bright fringe is observed. Assume D>>d.
View Solution
Knowledge Check
In figure, a screen is placed normaol to the line joining the two point coherent sources S1 and S2. The interference pattern consists of concentric circles.
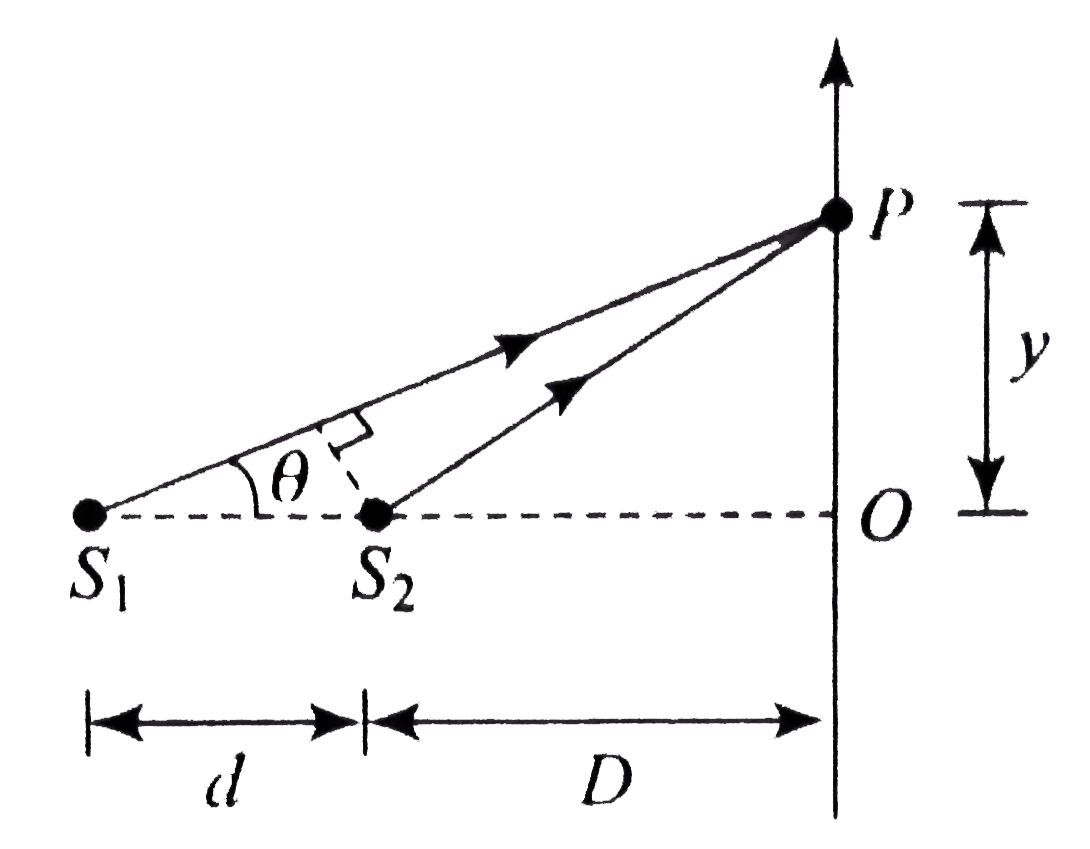
Also, find the value of radius for this ring.A6.32 cmB5.52 cmC4.7 cmD3.25 cmIn figure, a screen is placed normal to the line joining the two point coherent sources S1 and S2. The interference pattern consists of concentric circles.
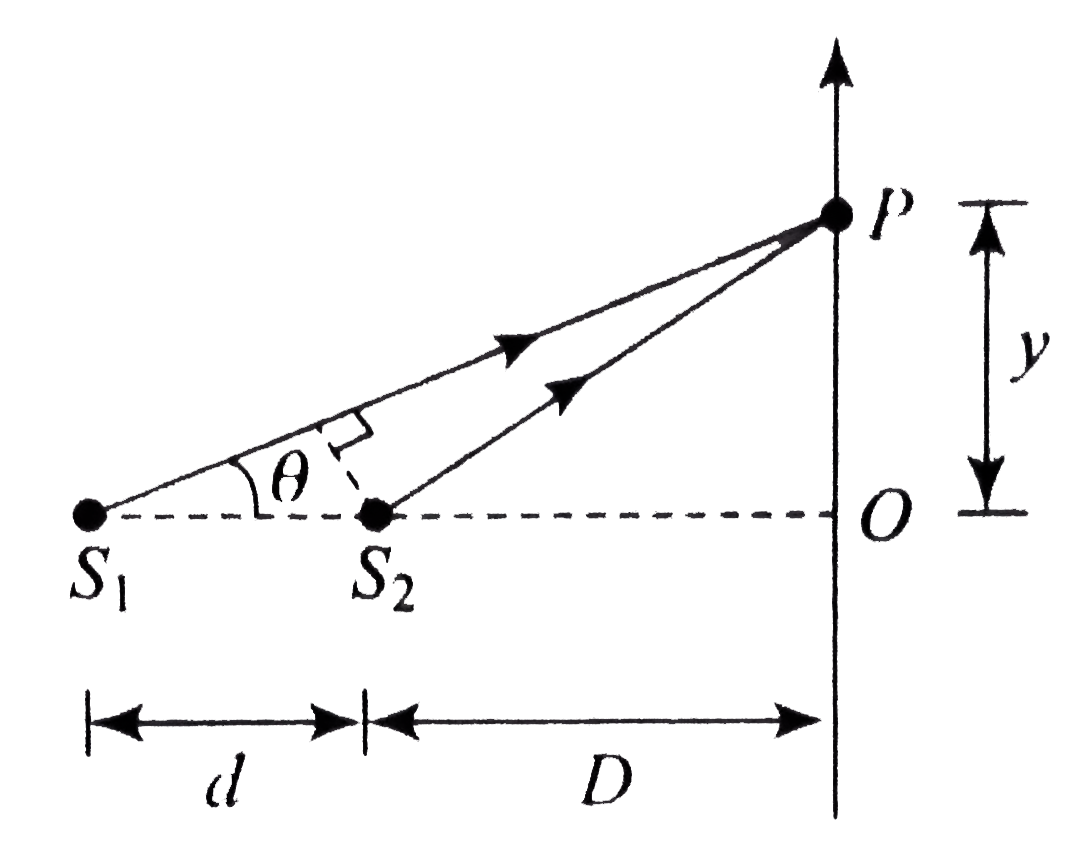
If d=0.5mm,λ=5000Å and D−10cm, find the value of n for the closest second bright ring.A888B830C914D998Two coherent sources of intensities I1 and I2 produce an interference pattern. The maximum intensity in the interference pattern will be
A(a) I1+I2B(b) I21+I22C(c) (I1+I2)2D(d) (√I1+√I2)2
Two monochromatic coherent sources of wavelength 5000 Å are placed along the line normal to the screen as shown in the figure.
(a) Determine the condition for maxima, at the point P.
(b)Find the order of the central bright fringe if d = 0.5 mm, D = 1 m.

View SolutionTwo coherent point sources S1 and S2 are located at a distance 4l from each other. Perpendicular to the straight line joining S1 and S2 there is a large screen at a distance of 1000 λ from S1 as shown in Figure. Find the radius of the third maxima starting from the point 0.
View SolutionIn Young's doulbe-slit experiment the separation between two coherent sources S1 and S2 is d and the distance between the source and screen is D. In the interference pattern, it is found that exactly in front of one slit, there occurs a minimum. Then the possible wavelengths used in the experiment are
View SolutionIn the case of light waves from two coherent sources S1 and S2, there will be constructive interference at an arbitrary point P, the path difference S1P−S2P is
View SolutionTwo coherent point sources S1 and S2 are separated by a small distance d as shown. The fringes obtained on the screen will be

View Solution

