In a YDSE using monochromatic visible light, the distance between the plate of slits and the screen is 1.7 m. At point P on the screen which is directly in front of the upper slit, maximum path is observed. Now, the screen is moved 50 cm closer to the plane of slits. Point P now lies between third and fouth minima above the central maxima and the intensity at P in one-fourth of the maxima intensity on the screen.
Find the value of n.
4
6
2
8
The correct Answer is:c
For point P in front of upper slit, y=d/2.
Initially, path diffence,
(d/2)dD=nλ
Intensity at any point on the screen is
I=Imax(1−cosϕ2)
(ϕ being the phase difference)
When the screen is placed, I=Imax4
Hence, cosϕ=12⇒ϕ=2nπ±π3
Also, as P lie between third and forth minima,
5π<ϕ<7π
From Eqs. (ii) and (iii), we get
ϕ=17π3 or 19π3
ϕ=(d/2)dD'2πλ=(nλD)D'2πD'=2nπDD'
=17nπ6 (putting the values of D and D')
∴n=2 or (38/17)
But n is integer, therefore n=2 is the only valid answer.
b. Putting the value of n and d in Eq. (i), we get λ=5.9×10−7m.
Topper's Solved these Questions
- WAVE OPTICSBook:CENGAGE PHYSICSChapter:WAVE OPTICSExercise:Integer
Explore 3 Videos
- WAVE OPTICSBook:CENGAGE PHYSICSChapter:WAVE OPTICSExercise:Archives
Explore 4 Videos
- WAVE OPTICSBook:CENGAGE PHYSICSChapter:WAVE OPTICSExercise:Assertion- Reasoning
Explore 13 Videos
- THERMODYNAMICSBook:CENGAGE PHYSICSChapter:THERMODYNAMICSExercise:QUESTION BANK
Explore 34 Videos
- WAVESBook:CENGAGE PHYSICSChapter:WAVESExercise:QUESTION BANK
Explore 38 Videos
Similar Questions
At a point on the screen directly in front of one of the slits, find the missing wavelengths.
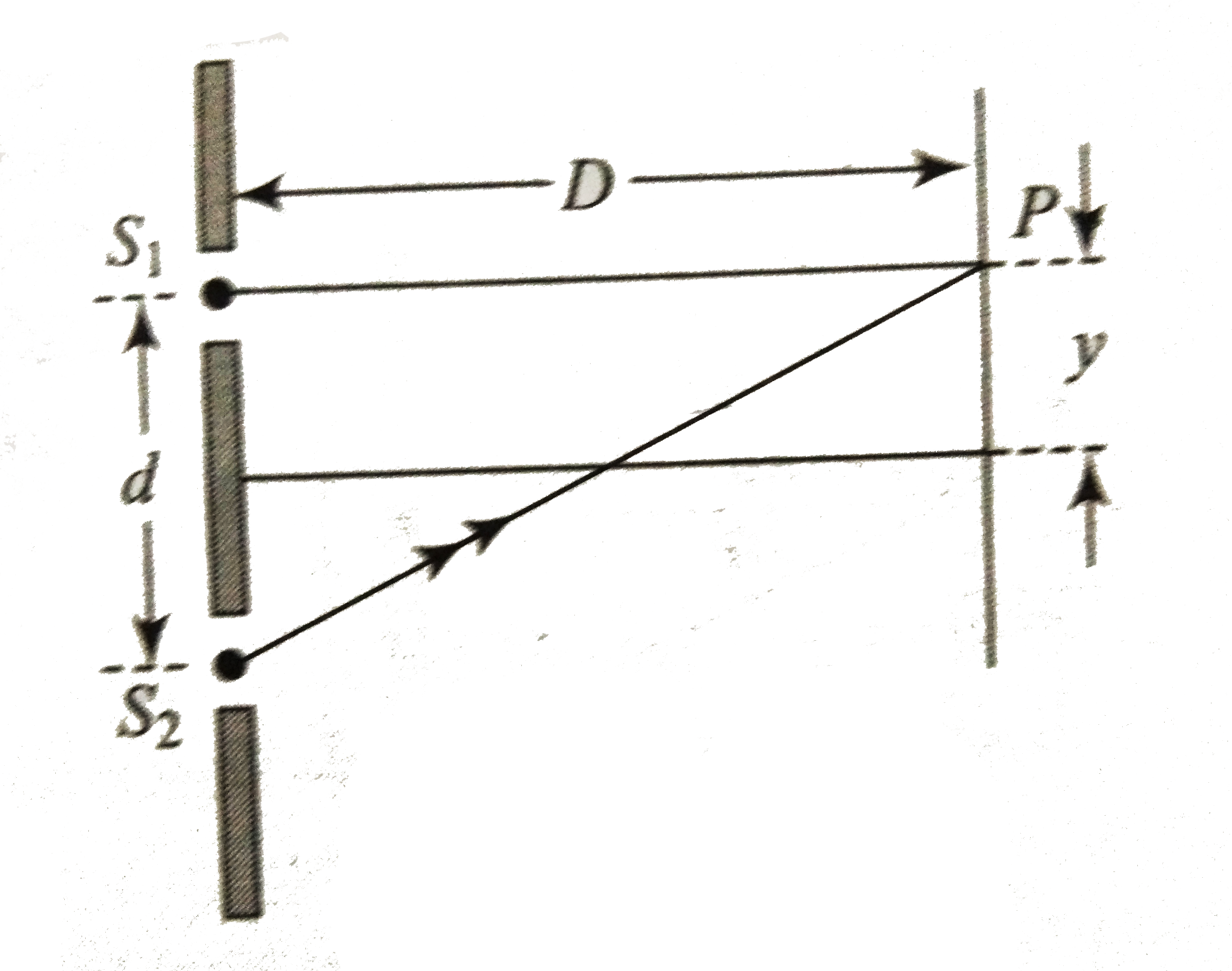
View SolutionIn Young's double slit experiment , the distance between double slit and the screen is 1 m . If the distance between two slits is 5 mm , the separation of successive maxima is found to be 0.1092 mm , calculate the wavelength of light used .
View Solution
Knowledge Check
In a YDSE using monochromatic visible light, the distance between the plate of slits and the screen is 1.7 m. At point P on the screen which is directly in front of the upper slit, maximum path is observed. Now, the screen is moved 50 cm closer to the plane of slits. Point P now lies between third and fouth minima above the central maxima and the intensity at P in one-fourth of the maxima intensity on the screen. ltbr> Find the wavelength of light if the separation of slits is 2 mm.
A2.9×10−7mB3.9×10−7mC5.9×10−7mD6.9×10−7mIn YDSE, water is filled in the space between the slits and screen. Then
AFringe pattern shifts upward but fringe width remains unchangedBfringe width decreases and fringe pattern shifts upwardCfringe width remains unchanged and central fringe does not shiftDfringe width decreases and fringe pattern does not shiftIn YDSE, separation between slits is 0.15 mm, distance between slits and screen is 1.5 m and wavelength of light is 589 nm, then fringe width is
A3.9mmB4.7mmC5.9mmD3.7mm
In Young's double-slit experment, the frist maxima is observed at a fixed point P on the screen. Now, the screen is continously moved away from the plane of slits. The ratio of intensity at point P to the intensity at point O (center of the screen)

View SolutionIn YDSE, the distance between the slits is 1 m m and screen is 25cm away from the slits . If the wavelength of light is 6000Å , the fringe width on the secreen is
View SolutionIn a single slit diffraction method, the distance between slit and screen is 1m. The size of the slit is 0.7mm and second maximum is formed at the distance of 2mm from the centre of the screen, then find out the wavelength of light.
View SolutionIn YDSE the distance between the slits is 1mm and screen is 25nm away from intensities IF the wavelength of light is 6000A the fringe width on the screen is
View SolutionIn Young's double slit experiment, the distance between the two slits is 0.1 mm, the distance between the slits and the screen is 1 m and the wavelength of the light used is 600 nm. The intensity at a point on the screen is 75% of the maximum intensity. What is the smallest distance of this point from the central fringe ?
View Solution

